

| ex1) AB=5,AC=3である三角形ABCがある.辺BCを2:1の比に内分する点をDとするAD=1である.辺BCの長さを求めよ. |
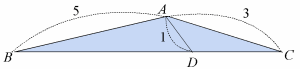 <かず子>三角比の問題ですね.三角形は右図のような形になるわ.
<かず子>三角比の問題ですね.三角形は右図のような形になるわ.
でも,どうやってBCを求めればいいかしら.
<よしお>点DはBCを2:1の比に内分する点だから,例えばBCの長さを3kとおいたらどうだろうか.
<かず子>そうね,そうすると BD=2k,CD=k となって計算し易いわね.
<よしお>それと,条件として AD=1 というのがあるからあとはこの扱い方だ.
<まなぶ>なに難しく考えてるの.三角比を使うのであれば,三角形ABDと三角形ACDの3辺の長さがkと数値で与えられているから当然余弦定理だろ.
<よしお>なるほどね.何となくわかってきたぞ.三角形ABDの∠ADBに,第3余弦定理を使えばいいんだ.
∠ADB=θとすると,
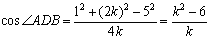
<かず子>そうすると,もう一つ式が必要だから,次は三角形ACDで余弦定理を使えばいいわね.
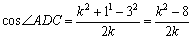
<まなぶ>ここで,∠ADC=180°-∠ADBという関係からあるから
cos∠ADC=cos(180°-∠ADB)=-cos∠ADB
だから,よしおとかず子の作った2式を辺々加えて,
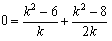
これから,k>0より,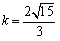
よって,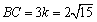
<先 生>三人寄れば文殊の知恵だね.図形問題を初等幾何とか三角比で解こうとすると,どうしてもいまみんなが解いたように,発想が要求されてしまう.まあ,それが面白みでもあるんだけどね.
<まなぶ>この問題は三角比では解かないぞって暗に先生はいってるわけですね.
<かず子>じゃあ,どうやって解けばいいのかしら.三角形の形が特殊だったらデカルト座標平面にその図形をおいて,簡単にできるのだけれど.
<よしお>そうだね.頂点の座標を決めて,
①2点間の距離(線分の長さ) ②分点の公式 ③点と直線の距離(ヘッセの標準形)
を使って求めればいいんだったよね.でもこの三角形の場合には座標はきめられないよね.
<まなぶ>Aを原点にして,辺ABをx軸上におけるけど,Cはどうしようもないよな.ACがy軸上にくるようにできれば最高なんだけどなあ.ACがy軸かぁ……,あっ,
<三 人>分かったぞ!!ベクトルだ.
 <先 生>おや,おや,ずいぶんシンクロしたものだね.その通り.
<先 生>おや,おや,ずいぶんシンクロしたものだね.その通り.
点Aを位置ベクトルの始点にして, ,
,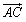 で張られる斜交座標を考えればいい.そうすると,二辺AB,ACが両軸にぴったりと重なる.それでは,
で張られる斜交座標を考えればいい.そうすると,二辺AB,ACが両軸にぴったりと重なる.それでは,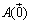 ,
,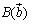 ,
,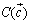 とすると,上の問題を書き換えるとどうなるだろうか.
とすると,上の問題を書き換えるとどうなるだろうか.
<まなぶ>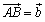 ,
,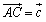 だから,
だから,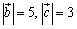
<よしお>次に点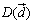 は,BCを2:1の比に内分する点だから,
は,BCを2:1の比に内分する点だから,
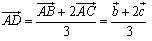 ,
,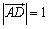 より,
より,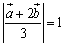
<かず子>で,求めるのものは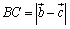 ですよね.
ですよね.
<先 生>結局,もともとの問題は次のように表現できる.
ex)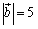 , ,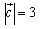 , ,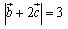 のとき, のとき,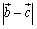 を求めよ. を求めよ.
|
<まなぶ>あれ,これベクトルの単元のところでやった問題だ.これならすぐにできるよ.
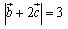 の両辺を平方して,
の両辺を平方して,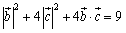
これから,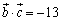
よって,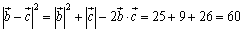
以上より,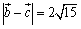
なんだ.めちゃくちゃ簡単ジャン.
<かず子>問題の表現の仕方でずいぶん難易度が変わるんですね.
<先 生>というより,一般に問題をベクトル化することは,発想のバイパスができるということなんだ.
<まなぶ>バイパス?
<先 生>例えば,もともとの問題で,次の追加した場合にどうやって求めればいいだろう.
| 辺BCの中点をE,辺ABを1:2の比に内分する点をFとするとき,EFの長さを求めよ. |
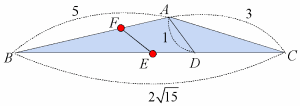 <よしお>うーん.結構大変ですね.BE,BFの長さはすぐ分かります.次に,三角形BEFに余弦定理を使えるようにするために,cos∠ABCを三角形ABCから求めます.
<よしお>うーん.結構大変ですね.BE,BFの長さはすぐ分かります.次に,三角形BEFに余弦定理を使えるようにするために,cos∠ABCを三角形ABCから求めます.
<先 生>でも,これをベクトルで考えると,そんな「解答の見通し」はまるで必要なくなる.まず,点E,Fの座標はどうなるだろうか.
<かず子>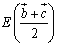 ,
,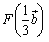 です.
です.
<先 生>求めるのはEFだから,ベクトルで表すと,
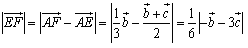
さあ,あとはこれを平方して計算してごらん.
<よしお>僕がやります.
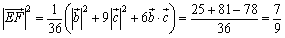
したがって,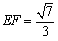 です.
です.
<先 生>この問題を解くためにみんながやったことはなにか整理してみよう.
まず,分点E,Fの位置ベクトルを求めて,次に を計算しただけだ.その計算は,
を計算しただけだ.その計算は,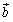 ,
,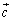 の大きさとその内積が分かっていればいい.したがって,図形上のどんな点であろうと,その点の位置ベクトルが分かれば単純計算で任意の2点を結ぶ線分の長さが求められてしまうということだ.
の大きさとその内積が分かっていればいい.したがって,図形上のどんな点であろうと,その点の位置ベクトルが分かれば単純計算で任意の2点を結ぶ線分の長さが求められてしまうということだ.
<まなぶ>へぇ.なんか凄いや.
<先 生>ではもう1題.
ex2)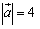 , ,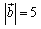 , ,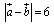 のとき, のとき,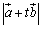 の最小値と,そのときの実数tの値を求めよ. の最小値と,そのときの実数tの値を求めよ.
|
<かず子>これもあとは,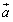 ,
,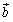 の内積が分かれば単純計算で求められるということですね.
の内積が分かれば単純計算で求められるということですね.
まず,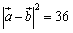 から,
から,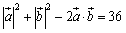 .よって,
.よって,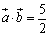 .
.
これから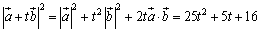
あとは平方完成して最小値を求めれば終りです.
<先 生>そうだね.
<まなぶ>……先生,それでいいの?
<先 生>なんだい,その探るような疑りの目つきは.
<まなぶ>だって,トラップがまるでないじゃないですか.先生からトラップをとったらあとには何も残らないですよ.
 <先 生>まなぶ.授業が終わってからゆっくり話し合おう.
<先 生>まなぶ.授業が終わってからゆっくり話し合おう.
繰り返すけど解答はこれでいい.でも問題があるとすれば,みんながこの問題がどんなことを要求していたか分からないうちに答えがでてしまっているということだ.この問題のベクトルを斜交座標系の点と考えて図形的に解釈するとどうなるだろうか.
<よしお>まず始点ですよね.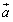 ,
,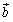 の大きさはそのままにしたいから適当に原点
の大きさはそのままにしたいから適当に原点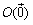 を作ります.そうすると,
を作ります.そうすると,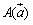 ,
,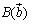 とできる.
とできる.
<かず子>そうね.よしおのように座標系を設定すると,
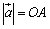 ,
,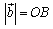 ,
,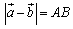
となるわ.
<まなぶ>ということは,この問題は三角形 を考えたとき,その3辺の長さが与えられているということですね.
あとは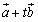 が何を意味するかということだけど…
が何を意味するかということだけど…
<よしお>これは直線のベクトル方程式だよ.点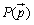 は,点Aを通り,
は,点Aを通り,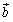 に平行な直線
に平行な直線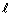 は,
は,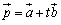 と表すことができる.
と表すことができる.
したがってこの問題は,原点と直線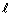 上の点を結ぶ線分の長さの最小値を求めよということですね.
上の点を結ぶ線分の長さの最小値を求めよということですね.
<先 生>まとめてみようか.
|
OA=4,OB=5,AB=6である三角形OABがある. 頂点Aを通り,線分OBに平行な直線 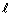 上の点をPとするとき,OPの長さの最小値とそのときのAPの長さを求めよ. 上の点をPとするとき,OPの長さの最小値とそのときのAPの長さを求めよ.
|
さて,問題をこのように図形問題に変えてしまうとその解答はどうなるだろうか.
<かず子>図から,最小となるのはOPが直線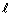 と垂直になるときだわ.これをベクトルで表現すると,
と垂直になるときだわ.これをベクトルで表現すると,
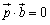
これから,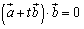 より,
より,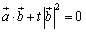 .
.
だから,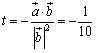 だわ.
だわ.
<まなぶ>その解き方だと結局はベクトル計算ではないだろうか.やっぱり三角関数で考えるべきだと思うな.僕なら,O から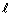 に下ろした垂線の長さが求めるものだから,これは,三角形ABCのOBを底辺としたのときの高さに等しい.この高さをだせばいいと思う.
に下ろした垂線の長さが求めるものだから,これは,三角形ABCのOBを底辺としたのときの高さに等しい.この高さをだせばいいと思う.
<かず子>なるほどね.そうすると,面積比較もひとつの手ね.
<まなぶ>高さと言えばやっぱりそうだよな.三角形ABCの面積はヘロンの公式で求められる.
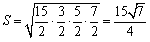
一方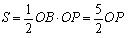
これを比較して,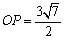
どうだい,できたぞ.
<よしお>でも,2人の解答は,最小値とtの値はそれぞれ求められたけど,残りの値をだすのに計算が必要になっしまうと思うな.
ここはやはりオーソドックスに余弦定理を使ってはどうだろうか.
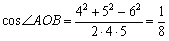
これから,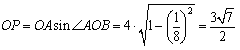
また, だから,もともとのtの値は,
だから,もともとのtの値は,
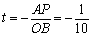
ということですね.
<先 生>三者三様の解答がでてきたよね.このように問題を図式化すると今度はその解法には発想が要求されてくるんだ.だから一般に問題が図形として与えられているとき,発想が沸かないときには,ベクトル化すると単純に計算できる.逆に,ベクトル化された式を解くときには,その図形的な意味に探りを入れてみるといい.こうやって天の邪鬼的に考えることは,多面的思考を養う上でも大切なことなんだよ.
<かず子>天の邪鬼的にねぇ.でも,そうするとどうしてまなぶは数学が苦手なのかしら.
<まなぶ>どういう意味さ.それ.
このように張られた平面では,直交座標系で与えれる次の諸公式(三種の神器)と同様のツールを使って,図形の性質を解析することが可能となります.
|
《図形解析Tools》 ①二点間の距離公式(線分の長さ) ②分点の座標 ③点と直線の距離(ヘッセの標準形) |
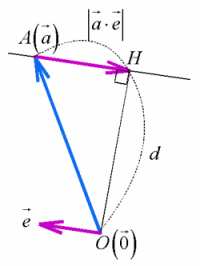 斜交座標系における,三種の神器を考えてみましょう.
斜交座標系における,三種の神器を考えてみましょう.
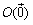 ,
,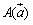 ,
,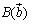 とします.
とします.
2点A,B間の距離は,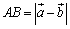 で与えられ,線分ABをm:nの比に分ける点
で与えられ,線分ABをm:nの比に分ける点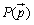 の座標は,
の座標は,
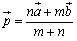
となり,直交座標と同様の式が与えられています.
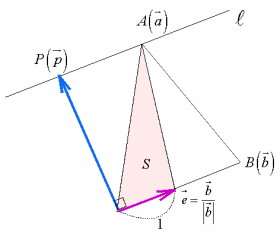
では,点と直線の距離の公式は,どうなるでしょうか.
点Aを通り方向ベクトル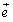 (単位ベクトル)である直線
(単位ベクトル)である直線
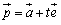
と原点Oとの距離dを考えてみましょう.
原点から直線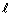 に下ろした垂線の長さがdですが,その足をHとすると,内積の定義より
に下ろした垂線の長さがdですが,その足をHとすると,内積の定義より
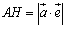
これから,
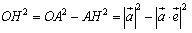 よって,
よって,
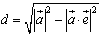
で与えられます.
 ここで,方向ベクトルを
ここで,方向ベクトルを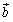 とすると,
とすると,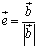 ですから,
ですから,
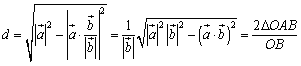
これは,本文でまなぶとかず子が考えた面積比較の形を現しています.
ベクトルは基底となる2つのベクトル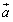 ,
,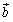 の大きさ(軸の基準値)およびベクトルのなす角を表す内積
の大きさ(軸の基準値)およびベクトルのなす角を表す内積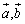 で斜交座標が決定するわけであるから,単位ベクトルよりも
で斜交座標が決定するわけであるから,単位ベクトルよりも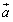 ,
,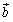 で公式を表現した方が使い勝手はいいことになります.
で公式を表現した方が使い勝手はいいことになります.
以上より,
|
《斜交座標の図形解析Tools》 平面上の3点を 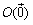 , ,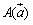 , ,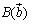 (ただし, (ただし,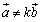 )とする. )とする.①2点AB間の距離…… 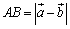 ②線分ABをm:nの比に分ける点 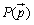 の座標 …… の座標 …… 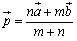 ③原点Oと直線 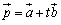 との距離d …… との距離d …… 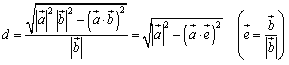
|
本文ex2の最小値は,
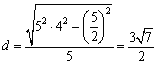
として求められるわけです.
このように,斜交座標系で考えることにより容易に求められる定理を紹介しましょう.
スチュワート(Stewart)の定理は幾何ではよく知られている定理です.
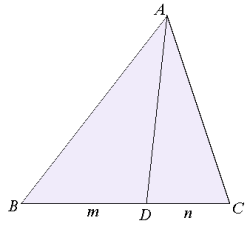 三角形ABCにおいて辺BCをm:nの比に内分する点をDとすると,
三角形ABCにおいて辺BCをm:nの比に内分する点をDとすると,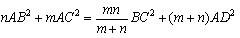 が成立する. |
いくつかの証明が考えられますが,代表的なのは三角比を利用したものです.
∠ADB=θとすると,三角形ABDにおいて余弦定理より,
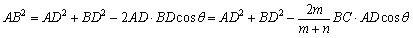 ……①
……①
同様に,∠ADC=180°-θであるから,三角形ACDにおいて余弦定理より,
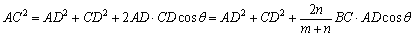 ……②
……②
①×n+②×mより定理が得られます.
なお,この定理の右辺を,
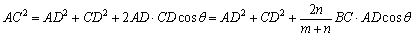
と変形すると,
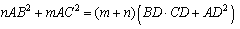
となります.また,
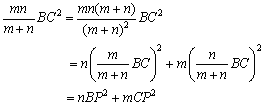
であることより,
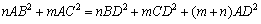
ここで,m=nとすると,点Dは辺BCの中点であり,BD=CDより,中線定理(Pappus)
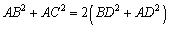
が得られます.スチュワートの定理は中線定理の拡張であるわけです.
では,この定理を斜交座標系で証明しましょう.
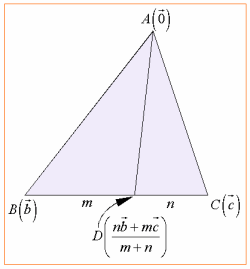
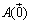 ,
,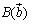 ,
,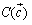 とし,
とし,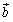 ,
,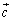 で張られる斜交座標系で考えます.
で張られる斜交座標系で考えます.
内積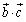 を求めます.
を求めます.
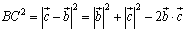 より,
より,

次に,内分点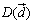 の座標は,
の座標は,
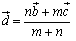 ……(*)
……(*)
これから,
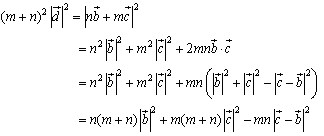
両辺をm+nで割りA,B,Cで表すと,
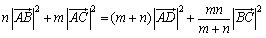
スチュワートの定理が証明されました.
証明の過程から,この定理は分点Dの座標(*)を変形しただけであることが分かります.
結局,スチュワートの定理は,分点Dの斜交座標系の値
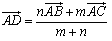 ……(**)
……(**)
を表していることになり,この式が定理のベクトル表示とみなすことができます.
本文のex1の解法は,幾何ではスチュワートの定理を利用すればいいことが分かると思います.
また,(**)では,点Dは外分点でも成立しますから,スチュワートの定理は
三角形ABCにおいて辺BCをm:nの比に外分する点をDとすると,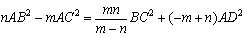 が成立する. |
と表されます.さらに,(**)の始点を点Dとすれば,3点A,B,Cが一直線上にある場合も定理は成立します.
このように,ベクトルでの証明の単純さは,定理の様々な拡張を見出すことができます.
 なお,高校数学では中線定理として使われる機会が多いわけですが,右図からこの定理をベクトルで表現すると,
なお,高校数学では中線定理として使われる機会が多いわけですが,右図からこの定理をベクトルで表現すると,
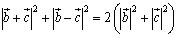
となります.
ところで,少しヒビが入っていたまなぶとかず子の関係.
本文の文末でかず子の強烈な一言.二人はどうなるのでしょうか.