
札幌旭丘高校 中村文則
○はじめに
点字は,3行×2列の6つの点の組合せにより構成される視覚障害者の為の文字である.
ただ,その点は視覚障害者には見ることはできないので,点を突起状に盛り上げて表現し,指の腹の感触で読み取っていくことになる.点字は,視覚的認知の文字ではなく,触覚で読む表音文字である.本当は,晴眼者(目の健常者)が認識する文字を凸状に盛り上げ,それを触って認識することができれば一番いいのだが,曲線で作られる文字は無限の形と大きさが可能であるため,単語として並べられたときにその前後の文字との区別が正確に判断できなくなってしまう.また,目は文字単位に追って「認識する」ことができるが,手は一つの文字の造りを追って「解読する」ところから始めなければならない.さらに,晴眼者側の凸上に加工するという技術的問題も生じてくる.こうしたことから,シンプルかつ実用的な文字体系を構築する必要が生じ,その試行錯誤の後,生まれたのが6つの点による表現なのである.
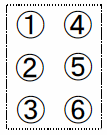 この3行×2列の枠はマスと呼ばれ,1行1列,2行1列,3行1列をそれぞれ「①の点」,「②の点」,「③の点」という.同様に2列目も上から順に,「④の点」,「⑤の点」,「⑥の点」と表す.そしてこの6つの点の組合せにより,「仮名」,「アルファベット」,「数字」等といった文字が表現される.
この3行×2列の枠はマスと呼ばれ,1行1列,2行1列,3行1列をそれぞれ「①の点」,「②の点」,「③の点」という.同様に2列目も上から順に,「④の点」,「⑤の点」,「⑥の点」と表す.そしてこの6つの点の組合せにより,「仮名」,「アルファベット」,「数字」等といった文字が表現される.
6つの点による表現は二進法としてみればもちろん 26=64通りであるが,ただこれは晴眼者にとっての場合の数である.前述のマスという枠は,晴眼者だけが見ることができるものであり,実際の点字にはない.凸上の点がまったくない状態の0は晴眼者にとってはひとつの数であるが,視覚障害者には何もない「空」であり,文字として読み取ることはできないのである.したがって,6つの点により構成可能な文字数は63通りということになる.これから,
五十音の仮名,26文字のアルファベット,0~9の数字
を表現するためには,文字構成に明確・正確な規則(アルゴリズム)がなければ到底不可能なのである.
ここでは,6つの点に打ち込められた思いをほんの少しだけ解析してみることにしよう.
なお,6つの点を本文では晴眼者に分かりやすいように
点を打つ(実点) ⇒ ● 点を打たない(虚点) ⇒ ○
と表すことにする.
1.数字を見る
①,②,④,⑤の点を使って,0から9の数字を表してみよう.
 まず,この4つの点で表現可能な文字数は何通りあるだろうか.
まず,この4つの点で表現可能な文字数は何通りあるだろうか.
24-1=15通り
と考えた貴方の脳はまだ晴眼者寄りにある.
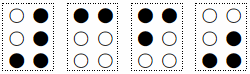
点を1つだけ打つ場合を考えて欲しい.その打ち方は①から⑥に打つ6通りであるが,視覚障害者はこの6つの点の区別は難しい.マスという枠の位置基準がないため,1マスのみで文字が表されていたり,列の片方のみに点があるマスが隣り合って並んでいれば,それらは別の文字と混同してしまう可能性がある.例えば,
 ⇒
⇒ や
や と区別できない
と区別できない

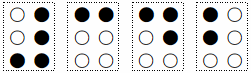
 ⇒
⇒ と区別できない
と区別できない
ということである.
そこで,1点のみを打つ場合は,1通りと考え,①の点をその代表として扱う.このとき,①の点は枠の左上カドにあるため,マスの基準位置としての役割も果たすことにもなる.
同様に考え,2点を打つ場合,例えば「①,②」と「④,⑤」の場合は同じとみなすと,
「①,②」(縦),「①,④」(横),「①,⑤」,「②,④」(斜め)
の4通りになる.
3点を打つ場合は,①,②,④,⑤のうち,点を打たない場所を考えるとそれらはみな異なる配置になる.したがって4通りである.
4点を打つ場合はもちろん1通りである.
以上より,①,②,④,⑤の4点で表現可能な文字数は,
1+4+4+1=10(通り)
である.これらの点の並べ方が0~9の数字にちょうどうまく対応させることができるのである.

2.ひとマスで表現可能な文字数
2行2列の4点では10通りの文字しか表現できないが,では,6点では何通りの表現が可能か考えてみよう.
点字は,1つのマスの中の点から文字を解読することから始まり,横に並べたマスを左から右の方向に読み進んでいく.上から下より,左から右の方が手の移動がラクだし,点の判別がし易いのだ.実は,この読み方のルールが自然とマスの形を3行2列に決定づけている.
2行3列の形のマスにした場合を考えると,横に単語が伸びてしまうだけでなく,
 の区別がし難い.また,晴眼者は単語全体やマスといったもので文字構成とか文字の大きさを読み取ることができるが,マスを認識できない視覚障害者にとっては文字の大きさは無意味であり,点と点の間にあるスペースが,マスの中のスペースか,マスとマスを隔てるスペースかの区別がつかないのである.
の区別がし難い.また,晴眼者は単語全体やマスといったもので文字構成とか文字の大きさを読み取ることができるが,マスを認識できない視覚障害者にとっては文字の大きさは無意味であり,点と点の間にあるスペースが,マスの中のスペースか,マスとマスを隔てるスペースかの区別がつかないのである.

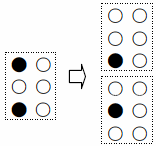 これは,もちろん,3行2列のマスにおいても,右図のように区別はできない.しかし,日常生活においては,点字は,エレベータの上・下の方向,ドアが開く,閉じるといった,固有名詞(単語,自立語ともいう)の認識に重点が置かれるため,横1行のマスの並びでセンテンスは終わる.生活空間を晴眼者と共有するためには,どうしても点字の読解は必要最小限のことを的確に理解することだけに制限されてしまう.したがって,改行する場合はあまり考える必要はないのである.また,点字で長い文章を読み改行がある場合においては,その改行幅を大きくとればいいことになる.だから,3行2列のマスにおいては,横のスペースは,マスとマスを隔てるものであり,縦のスペースは,点と点を隔てるものであると解釈すればよいのだ.
これは,もちろん,3行2列のマスにおいても,右図のように区別はできない.しかし,日常生活においては,点字は,エレベータの上・下の方向,ドアが開く,閉じるといった,固有名詞(単語,自立語ともいう)の認識に重点が置かれるため,横1行のマスの並びでセンテンスは終わる.生活空間を晴眼者と共有するためには,どうしても点字の読解は必要最小限のことを的確に理解することだけに制限されてしまう.したがって,改行する場合はあまり考える必要はないのである.また,点字で長い文章を読み改行がある場合においては,その改行幅を大きくとればいいことになる.だから,3行2列のマスにおいては,横のスペースは,マスとマスを隔てるものであり,縦のスペースは,点と点を隔てるものであると解釈すればよいのだ.
では,どれだけの点の組合せが可能か調べてみよう.
打つ点の個数で場合分けをする.
まず1点の場合は,①~⑥のどこに打っても同じとみなせるから1通りである.
2点の場合は,その2点が一つの列に配置されるか,2列のどちらにも配置されるかでさらに場合分けをしていく.
1列の場合は,「①,②」,「①,③」に代表される2通り.2列の場合は,2点を結ぶ傾きを考えて,
「①,④」,「①,⑤」,「①,⑥」,「②,④」,「③,④」
の5通りである.よって総数は7通り.
3点の場合も1列のみの配置と2列にまたがる配置の場合について考えよう.
1列の場合は「①,②,③」の1通り.
2列は,1列目が1つの点の場合では,
 の7通りである.1列目が2点,2列目が1点でも同様の場合があるから,総数は15通りである.
の7通りである.1列目が2点,2列目が1点でも同様の場合があるから,総数は15通りである.
4点の場合は,1列目が1点の場合は,2列目はすべて点を打つことになるから3通り.同様に1列目が3点の場合も3通りである.
1列目,2列目ともに2点の場合は,
 の8通りとなる.したがって総数は,14通りである.
の8通りとなる.したがって総数は,14通りである.
5点の場合は,打たない1点の位置を考えれば6通りである.
6点の場合は1通りである.
以上より,その総数は,
1+7+15+14+6+1=44(通り)
である
3.仮名文字をみる
五十音は,や行,わ行を除くと,各5文字ずつあるから,
5×8=40 (文字)
である.これに,「や,ゆ,よ」,「わ,ゐ,ゑ,を」,「ん」を加えると48文字で,6点で表現可能な文字数をオーバーしてしまう.したがってこれらの文字に関しては特別な扱いをしなければならないことが予想される.まず,最初は「あ,か,さ,た,な,は,ま,ら」の行について考えてみよう.
実は,点字は,ローマ字の様に「母音」と「子音」の組合せで1つの仮名文字を表現するようになっている.では,その母音,子音は①~⑥のどの点に対応させればよいだろうか.
母音の数は5個,これに対して,行の数は「あかさたなはまら」の8行である.どうだろう?.
???????????????????????????????????????????????
5個と8個の個数を単純に2進法で表現するには であるから3点が必要ということになる.
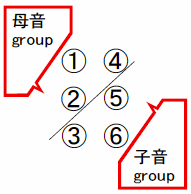 したがって,6点は,3点+3点に分けるしかないことは明らかである.ただし,3点を縦1列とし,1列,2列で分けると,1列にある3点が表現できる値は2通りしかないわけだから,この分け方では無理である.よって,3点は,
したがって,6点は,3点+3点に分けるしかないことは明らかである.ただし,3点を縦1列とし,1列,2列で分けると,1列にある3点が表現できる値は2通りしかないわけだから,この分け方では無理である.よって,3点は,
A:「①②④」と「③⑤⑥」 または B:「①④⑤」と「②③⑥」
以外に分けることができない.実際,点字はAの形によって,「①②④」が母音,「③⑤⑥」が子音を表し,その組合せで仮名文字を表現している.
母音を表す「①②④」の3つの点で識別可能な組合せを,打つ点の個数で場合わけをして考えると,
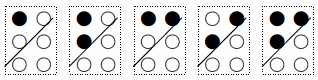 5通りであり,これは母音の個数に一致するのである.
5通りであり,これは母音の個数に一致するのである.
そこで,左側のマスから順に
「あ,い,う,お,え」
と対応させる.
次に「③⑤⑥」で表す子音であるが,3つの点から表現可能な文字数は母音と同じく5通りであるが,,この場合はすでに母音が確定しているために,それに対応する子音は,母音の位置によってすべて区別がつけられてしまう.よって,空の場合も含めて, 通りの表現が可能となる.そして,この個数は子音「あかさたなはまら」の個数に一致する.
その8通りを点の数で場合分けし,書き抜くと,
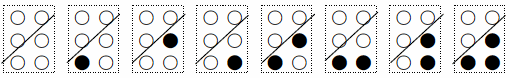 これを左側から順に,
これを左側から順に,
「あ,な,ら,か,た,は,さ,ま」
に対応させる.
あとは,母音と子音を表す点のマトリックスから仮名40文字を読み取っていく.
例えば,「うれしい」を点字で表すと,
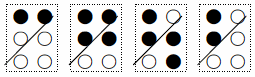 である.
である.
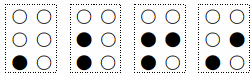
では,次に,残りの「や,ゆ,よ」,「わ,ゐ,ゑ,を」,「ん」の点字を作ってみよう.
「や行」は,まず,対応する母音の点の組を行方向(下)に可能な限り降ろす.
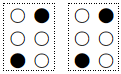
①(あ) ⇒ ③ ①④(う) ⇒ ③⑥ ②④(お) ⇒ ③⑤
そして,④の点を打ち,「や,ゆ,よ」に対応させる.
 なお,この3つのマスの並びは,先ほど調べた6点で表現可能な44通りの中に含まれるものである.
なお,この3つのマスの並びは,先ほど調べた6点で表現可能な44通りの中に含まれるものである.
また「わ行」は,対応する母音の点の組を行方向に可能な限り降ろしたものを「わ,ゐ,ゑ,を」に対応させる(ゐ,ゑについては現在では使われていないから必要はないのだが).
 もちろん,この並びは,「あ,い,え,お」と1マスでは区別がつかないから実際はその前後のマスの文字と比較して判断しなければならないが,「わ行」で単独で単語を表すものは「わ(輪,和)」ぐらいであり,これと類似する「あ」については単語として読むことは余りないからそれほど問題はないはずである.
もちろん,この並びは,「あ,い,え,お」と1マスでは区別がつかないから実際はその前後のマスの文字と比較して判断しなければならないが,「わ行」で単独で単語を表すものは「わ(輪,和)」ぐらいであり,これと類似する「あ」については単語として読むことは余りないからそれほど問題はないはずである.
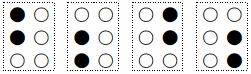
最後に「ん」(撥音)は,
 と表す.これは,「ろ」
と表す.これは,「ろ」
 と類似するが,「ん」自体が単独で表されることがないから,前後の文字で判断するということになろう.
と類似するが,「ん」自体が単独で表されることがないから,前後の文字で判断するということになろう.
ちなみに,撥音に対して,詰まる音(促音)「っ」,伸びる音(長音)「-」は,

 で表す.
で表す.
以上で,点字による仮名文字の対応が完成する.別表に「点字による五十音表」として掲げたので参照されたい.
4.2進法の並びから仮名を拾い出す
①②③④⑤⑥の点を2進法でこの順に位が高くなるとみて,すべての数を書き表すと右図のようになる.
 この表において,2進法の小さい数を表すマスの最初に出現する配列と同じ文字とみなすことのできるものすべてに「×」をつけてみよう.
具体的にいうと,
この表において,2進法の小さい数を表すマスの最初に出現する配列と同じ文字とみなすことのできるものすべてに「×」をつけてみよう.
具体的にいうと,
 はみな同じ配列と見なせるから,2進法で表したときに一番小さな数を表す左端のマス以外にすべて「×」をつけていく.
はみな同じ配列と見なせるから,2進法で表したときに一番小さな数を表す左端のマス以外にすべて「×」をつけていく.
すべてチェックが終わったら,次に,点字が表す五十音をマスに記入する.先ほどの例では,「①②」を表す「い」をマスの上に書く.すると,五十音をすべて書き終えた後,1つだけ「×」も「文字」も書かれていないマスが残る.そのマスの中の点の配列は何だろうか.
??????????????????????????
点字と五十音を対応させたときに,「わ行」と「ん」を除くと,43文字が相当することが分かるが,6点で表現可能な配置は44通りであった.したがって,まだ使われていない配置が1つ存在することになるのである.上述の「エラトステネスのふるい」のような作業はそれを見つけ出すものであるが,同時に,五十音の文字の配列についてもよく見て欲しい.必ずしも,点字は2進法の数字の大小に完全対応させた並びにはなっていないが,母音と子音の組合わせでルールが作られるから,当然配列にその規則性が反映されるのである.
別表に解答を載せたので確認願いたい.
ここでは,最後に残った1つのマスの配置が何なのかだけを示そう.
 その並びは「逆L字」の形になっている.
その並びは「逆L字」の形になっている.
5.再び数字を見る
仮名文字の表現のところで変だと思った方がいるだろう.仮名文字と数字の配列がダブってしまっているのである.
数字「1,2,3,4,5,6,7,8,9,0」と,仮名「あ,い,う,る,ら,え,れ,り,お,ろ」はまったく同じ配列であるから,このままでは読んだときにその区別をつけることはできない.そこで,使用頻度の高い仮名文字の方を上述の配列として決め,数字に関しては,「数字と分かるようなルール」を作ることにする.そのルールは点字では,宣言符の形で数字の前に前置すればよい.実は,「逆L字」がそれにあたる.五十音のどれにも該当していない逆L字が認識されたらそれ以降のマスの配置は数字と見なすのである.この数字の宣言符を「数字符」という.
例えば,314は,
 と表すことになる.逆に,数字から仮名文字への切り替えは通常は,そのまま平仮名を表す点字を続けて書いていけばよい.
と表すことになる.逆に,数字から仮名文字への切り替えは通常は,そのまま平仮名を表す点字を続けて書いていけばよい.
 は「34にん」と認識される.すなわち,「にん」の「に」と同じ配列の数字がないことより,仮名への切り替わりが自動認識されるのである.
は「34にん」と認識される.すなわち,「にん」の「に」と同じ配列の数字がないことより,仮名への切り替わりが自動認識されるのである.
問題は,数字と同じ配列である「あ,い,う,る,ら,え,れ,り,お,ろ」,すなわち「あ行」と「ら行」が続く場合である.「えん(円)」や「るい(塁)」が数字であるとき,切り替えの判断が難しくなる.
 は,「3えん」あるいは「36ん」と読めるが,後者の読みはあり得ないからどうにか判断できる.しかし,
は,「3えん」あるいは「36ん」と読めるが,後者の読みはあり得ないからどうにか判断できる.しかし,
 となると,「342」,「3るい(塁)」,「34い(位)」,どれも可能性のある言葉に読み取れてしまう.そこで,「あ,ら行」が続く場合だけ,仮名に変えることを表す宣言符をつけることにする.アンダーバーの形に似た,
となると,「342」,「3るい(塁)」,「34い(位)」,どれも可能性のある言葉に読み取れてしまう.そこで,「あ,ら行」が続く場合だけ,仮名に変えることを表す宣言符をつけることにする.アンダーバーの形に似た,
 がそれにあたり,「つなぎ符」という.例えば,「34位」は,「34_位」とみなし,
がそれにあたり,「つなぎ符」という.例えば,「34位」は,「34_位」とみなし,
 と表される.
と表される.
6.宣言符による文字変化
数字符,つなぎ符が仮名文字と数字の切り替えを表したように,他の文字種に変換する宣言符は他にもいろいろある.
「きゃ,きゅ,きょ」のように「ゃ,ゅ,ょ」をついた拗音は,宣言符
 をつけることで,「か,く,こ」が,「きゃ,きゅ,きょ」に転じる.
をつけることで,「か,く,こ」が,「きゃ,きゅ,きょ」に転じる.
 同様に,濁音「゛」や半濁音「「゜」は「゛,゜」を表す宣言符をつけて,2マスで表現する.
同様に,濁音「゛」や半濁音「「゜」は「゛,゜」を表す宣言符をつけて,2マスで表現する.
拗濁音「ぎゃ,ぎゅ,ぎょ」や拗半濁音「ぴゃ,ぴゅ,ぴょ」は,それぞれ「拗音+濁音」,「拗音+半濁音」とみて宣言符をつくる.
 また,アルファベットの宣言符は,
また,アルファベットの宣言符は,
 であり,これに続いて,アルファベットを表す配列のマスを書く.この宣言符を外字符という.
であり,これに続いて,アルファベットを表す配列のマスを書く.この宣言符を外字符という.
なお,アルファベットは,数字「1~9,0」を表す配列が,「A~J」を表し,③の点を打つと,「K~T」,さらに③,⑥の点を打って,「U~Z」を原則として表すことにする(Wで少しずれるが).
また,アルファベットを英語の綴りと考える場合には,外国語引用符,
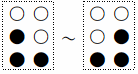 の間に単語を表す点字を入れる.さらに,大文字を表すには,大文字符
の間に単語を表す点字を入れる.さらに,大文字を表すには,大文字符
 によって,宣言をする.
によって,宣言をする.
このように,6点字で表現できる文字数は制限されているから,多種の文字を表現するために,このように文字種変換を宣言する符号が必要なのである.
これは,コンピュータのキーボードが,「Alt」,「Shift」,「Ctrl」を押すことによって,1つのキーにいくつかの文字が割り当てられていることと同じである.しかし,宣言符は,「逆L字」の数字符を除き,6点で表現される44文字以外の配置となるため,前後のマスの配置をよく見ないと,宣言符であることの判断が難しい.点字は解読が伴う文字であることを痛感させられるのである.
7.計算を試みる
2進法は,0,1からなる数字的言語であり,その言語の中で,四則演算を解析・処理することができる.これに対して,点字は,日本語を6点に凝縮した補助的中間言語であり,読解された点字の解析は他の言語体系(日本語)で思考される.したがって,点字自体には解析処理能力があるわけではないから,点字のままで計算することはできない.ここでは,単に点字を使って数の四則演算がどう表現されるかということのみについて触れる.
数字について,「逆L字」の数字符を宣言することで「あいうるらえれりおろ」の点字が対応することは既述した.
小数については,小数点を表す点字
 を挟むが,①点の「あ」,「1」,「a」と②点の「小数点」の違いは,数字符,外字符やその前後のマスの配置から判断することになる.
を挟むが,①点の「あ」,「1」,「a」と②点の「小数点」の違いは,数字符,外字符やその前後のマスの配置から判断することになる.
例えば,「3.14」は,
 と表される.
と表される.
分数は,基線(/)を表す符号,
 を挟む.分数 3/4は,
を挟む.分数 3/4は,
 である.この基線を2つ並べると
である.この基線を2つ並べると
 割り算を意味する.割り算(除法)とその結果のひとつである分数が点字でもきちんと区別されているのである.
割り算を意味する.割り算(除法)とその結果のひとつである分数が点字でもきちんと区別されているのである.
加法(+),減法(-),乗法(×),等号(=)は,それぞれ
 加法と減法,乗法と除法(分数)を表す点字が対の形で表現されているのが分かる.
加法と減法,乗法と除法(分数)を表す点字が対の形で表現されているのが分かる.
これらを組合せることで点字で簡単な四則演算を表現することができる.
 点字が,演算には向かない標記であることがよく分かる.もっと複雑な計算は小・中・大括弧をつけて演算の優先順位を決めることになるが,別表にそれらの表記符を載せておいた.
点字が,演算には向かない標記であることがよく分かる.もっと複雑な計算は小・中・大括弧をつけて演算の優先順位を決めることになるが,別表にそれらの表記符を載せておいた.
○あとがき …… 点字の実際
本文では,簡単に点字の生成とそのルールを述べた.しかし,実際は,これだけのことで点字がスラスラ読める訳ではない.前述したが,点字は視覚的に認知することはできない.晴眼者が文章を読めるのは,文章の文字種が非常にバラエティに富んでいることもある.カタカナがあったり,数字があったり,漢字があったりすると,晴眼者の目は自動的にその後の文字種を読み替えていく.しかし,表音文字である点字はそのことが大きな障害となってしまう.「あすはいしゃにいく」が,「あすは,いしゃにいく」と「あす,はいしゃにいく」では違った意味に取れてしまうのはよくある例である.
そのため,点字には句点,読点以外に,単語と単語の間に「分かち書き」(マス空け)と呼ばれるスペースを入れて読みやすくし,誤読を防ぐ工夫がされている.また,晴眼者の見る文章は助詞などが多少間違って表現されていてもその前後で文脈を読むことはできるが,点字での間違いは場合によっては生命の危険も伴う場合もある.そのために「点字文法」があり,それをきちんと熟知していないと,点字を理解することなど不可能である.それを身をもって体験したければ,目をつぶって10歩ほど歩いてみればよい.騒音の中に,手探り,足探りで身動きできなくなる自分を発見するはずである.
視覚を奪われることは,「行動の予知」ができなくなることでもある.歩きながら歩道に目を移すと,凸状の黄色く塗られたデコボコした帯が,交差点,信号機の下の路面にあるのは誰でも知っている.ただ,晴眼者でそのデコボコを意識して歩く人は少ないと思う.この黄色の帯は,点字ブロックと呼ばれ,視覚障害者に注意を呼びかけたり,誘導したりする記号である.点字が手の感触で読解するなら,点字ブロックは足の裏(あるいは指)の感触で識別する簡易言語であり,道路標識である.黄色いのは視力の悪い人にとってはこの色が見やすいからである.
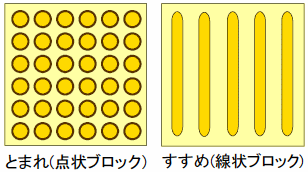 デコボコの形状によって,右のように点字ブロックは2つの意味「進め」,「止まれ」を表す.多くの場合,この点字ブロックは2種類の組合せで使われる.視覚障害者は「行動の予知」ができないから,いきなり足が「止まれ」のブロックを認識したしたとすると,危険が先にあるかもしれないという不安で精神的に動揺する.そこで,最初に「進め」のブロックを提示し,いつ表示が切り替わるかを足で予測させるのである.晴眼者は「止まれ」の標識をその位置まで着く前に視覚認識してしまうのと感覚が異なっているところである.
デコボコの形状によって,右のように点字ブロックは2つの意味「進め」,「止まれ」を表す.多くの場合,この点字ブロックは2種類の組合せで使われる.視覚障害者は「行動の予知」ができないから,いきなり足が「止まれ」のブロックを認識したしたとすると,危険が先にあるかもしれないという不安で精神的に動揺する.そこで,最初に「進め」のブロックを提示し,いつ表示が切り替わるかを足で予測させるのである.晴眼者は「止まれ」の標識をその位置まで着く前に視覚認識してしまうのと感覚が異なっているところである.
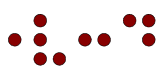 もう1例をあげると,右の点字はビール缶のタブ(リングプル)近くに打たれているものである.もちろん「ビール」と書いてある.この点字は,いま手に持っている缶がビールという商品を示すということをいっているだけではない.ジュースのような清涼飲料水には点字はついていないので,このビールの点字は,「この商品はジュースではありませんよ」という注意・警告ともとれる.未成年者の誤飲防止といった意味もあるのだろう.
もう1例をあげると,右の点字はビール缶のタブ(リングプル)近くに打たれているものである.もちろん「ビール」と書いてある.この点字は,いま手に持っている缶がビールという商品を示すということをいっているだけではない.ジュースのような清涼飲料水には点字はついていないので,このビールの点字は,「この商品はジュースではありませんよ」という注意・警告ともとれる.未成年者の誤飲防止といった意味もあるのだろう.
これも視覚障害者は,「その缶を飲んでみないと中身が何なのか分からない」からである.「読まない」と,「歩かない」と,「飲まない」と分からないことを晴眼者が分からなければ点字規則の理解は難しいのではないだろうか.
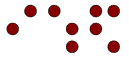 ちなみに,ビールの缶には右の点字が打たれていることもある.これは何と読むだろうか.
ちなみに,ビールの缶には右の点字が打たれていることもある.これは何と読むだろうか.
ところで,もともと点字は,フランスの砲兵大尉,シャルル・バルビエが,戦場において,闇夜でも分かる通信暗号として考えたものである.これを後に同じフランス人ルイ・ブライユが改良し,現在の点字の原形といえるものを考案した.ブライユは3才の頃に誤って鋭利なもので眼を突き片眼を失明し,やがて残りの眼も見えなくなる.盲目でありながら彼は視覚障害者が「手で見る」ことのできる6点マスの点字を作り出したのである.
彼の考案した点字はやがて日本に伝わるが,日本語でも使えるように仮名五十音に対応させるための研究が続けられる.そして,1890年(明治23年)11月1日,4回に及ぶ点字選定会の討議・実験を経て,盲唖学校の教員であった石川倉次氏の案が採択された.石川氏は,晴眼者でありながら,点字を利用する側に立った合理的ルールを考案し,日本語での6点点字を完成させる.宣言符により,文字種を切り替えたり,清音を濁音,拗音に変転させるといった発案は当時では斬新的なものであり,視覚障害者の前に閉ざされていた自立・学問の道への扉を開け放ったのである.
ちなみに,氏は「点字教育の父」と呼ばれ,その偉業を称えて,11月1日は「日本点字制定記念日」に制定されている.
 この後,日本の点字は独自の発展を遂げていき,「6点漢字」,「漢点字」といった漢字の分野にまで進出していくが,その普及と並行して書物を点字に翻訳(点訳)する必要性が生じてくる.点字に対して晴眼者の読む文字を総称して墨字というが,この墨字を点字に書き換えるのは実は大変な作業なのである.墨字を点字に直すには,原稿用紙を点字盤の上に乗せ先端が針状になった点筆と呼ばれる道具で,用紙に垂直に打って窪みをつけていく.これを裏返しにすると点が凸状に膨らんだ点字ができる.だから,点字を書くときには裏返しになることを考え,右から左の方向に,さら「読む点字」に対して鏡面対称に配置された点字を打たなければならない.「読む点字」と「書く点字」は,行方向,点字の配置ともに異なっているのである. 近年は,点字タイプライターやコンピュータソフト(ういんびー)に代表される)による出力も可能になったがそれでもその手間と労力は大変なものといえるだろう.
この後,日本の点字は独自の発展を遂げていき,「6点漢字」,「漢点字」といった漢字の分野にまで進出していくが,その普及と並行して書物を点字に翻訳(点訳)する必要性が生じてくる.点字に対して晴眼者の読む文字を総称して墨字というが,この墨字を点字に書き換えるのは実は大変な作業なのである.墨字を点字に直すには,原稿用紙を点字盤の上に乗せ先端が針状になった点筆と呼ばれる道具で,用紙に垂直に打って窪みをつけていく.これを裏返しにすると点が凸状に膨らんだ点字ができる.だから,点字を書くときには裏返しになることを考え,右から左の方向に,さら「読む点字」に対して鏡面対称に配置された点字を打たなければならない.「読む点字」と「書く点字」は,行方向,点字の配置ともに異なっているのである. 近年は,点字タイプライターやコンピュータソフト(ういんびー)に代表される)による出力も可能になったがそれでもその手間と労力は大変なものといえるだろう.
話を戻そう.本文では,点字の構成が数理的にどう分析できるか調べてみた.結果,僅か6つの点が実に見事に配置されていることに驚かされた.しかし,この配置がもともと「そうなるように」考案されたかというと,そうではないと思う.石川倉治氏が考えた点字の基盤はブライエの6点点字であるが,ブライエは,数字とアルファベットを点字で表現することから始めた.(さらには,音符を点字化し,楽譜を読んだり作曲したりすることも試みた).フランス語ではWの文字があまり使われることがなかったため,この文字だけが,アルファベットの順番通りにならなく,特別な位置に配置される.石川氏は,ブライユの配置を尊重し,これをベースにして,五十音の配置を考えていく.当時の閉鎖的時代にあって,氏は日本の将来の国際化を信じて疑わなかったのであろう.このため,五十音の配置は,母音,子音ともズレが生じているのである.
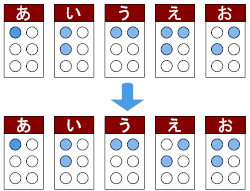 ただ母音に関して,もう一度その配置の順番を見てみよう.母音「あ,い,う,え,お」を点の個数で場合分けして並べていくならば,「え」と「お」だけを並べ替えたらきれいに配置されることに気がつく.この程度の入れ替えはブライエの点字を基にしてもなんら影響はなかったはずだし,その方が視覚障害者にとってもずっと覚えやすいはずなのだ.では,石川氏と点字選定会のメンバーは,なぜこの部分を問題にしなかったのだろうか.
ただ母音に関して,もう一度その配置の順番を見てみよう.母音「あ,い,う,え,お」を点の個数で場合分けして並べていくならば,「え」と「お」だけを並べ替えたらきれいに配置されることに気がつく.この程度の入れ替えはブライエの点字を基にしてもなんら影響はなかったはずだし,その方が視覚障害者にとってもずっと覚えやすいはずなのだ.では,石川氏と点字選定会のメンバーは,なぜこの部分を問題にしなかったのだろうか.
子音「ま」行と母音「え」に対応する文字,すなわち「め」の点字を点字表で見てみよう.右の配置の文字である.点を結んでみると,この字はなんとなく漢字の「日」に見えてくる.視覚障害者は見ることのできないけれど,晴眼者は見ることのできる晴れた日の「光」がこの点字には含まれている.また,6点すべてが凸点であるこの字は触ったときにもっとも判断しやすい文字であり,その形状は「目」の字にも似ている.だから,視覚障害者が,「め」の点字に触れると,「目が見える」のである.視覚障害者は,「め」を通して,点字が日本語と彼らをつなぎ,晴眼者と彼らを結ぶものであることを知り,自分達の本当の心の「目」に触れるのだ.
 石川倉治氏は,多少の五十音のずれよりも,視覚障害者が「め」を触ったときの感動と安らぎを大切にし,「め」がこの配置になることを何よりも優先したのだろう.
石川倉治氏は,多少の五十音のずれよりも,視覚障害者が「め」を触ったときの感動と安らぎを大切にし,「め」がこの配置になることを何よりも優先したのだろう.
私たちは110年の時を経て,彼の熱く,優しい思いに触れるのである.
<参考文献>
- 等山 啓著 「点字・点訳基本入門」 (二期出版)
- ※点字器の画像は,「社会福祉法人 日本点字図書館」ホームページ(www.nittento.or.jp)より転載
○訂正並びに謝辞
本稿が数実研ホームページに掲載された直後,
筑波大学附属盲学校の遠藤利三先生
よりご丁寧なメールをいただき,本稿の内容の誤り,および表現等を改めた方がいい箇所について,ご指摘・ご助言をいただきました.
下記がその内容です.
(箇所) 表題の「点字を数学的に読み取る」の点字パターン
(内容) 分かち書きがされていないことと,数学の「う」が長音になっていないことの訂正.
|
(箇所) ○はじめに
点字は,3行×2列の6つの点の組合せにより構成される視覚障害者の為の言葉である.
(内容) 下線の「言葉」を「文字」に訂正
|
(箇所) 5.再び数字を見る
「数字「1,2,3,4,5,6,7,8,9,0」と,仮名「あ,い,う,る,ら,え,れ,り,お,ろ」はまったく同じ配列であるから,このままでは視覚障害者は区別をつけることはできない.」
(内容) 区別をつけることができないのは視覚障害者だけではないので下線の部分を「読んだときにその区別をつけることはできない.」と訂正.
|
(箇所) 5.再び数字を見る
「問題は,数字と同じ配列である「あ,い,う,る,ら,え,れ,り,お,ろ」,すなわち「あ行」と「ら行」が続く場合である.「えん(円)」や「るい(塁)」が数字であるとき,切り替えの判別が難しくなる.」
(内容) 下線の部分は,切替を行わないのがルールであるため,それ以後の文章も含めて訂正しました.
|
(箇所)7.計算を試みる
分数は基線(/)を表す符号……
(内容)基線(/)を表す符号で表現できる例として,3/4を挙げていますが,分母の4の数符が抜けていました.
|
ホームページ数学いずみは,近年,投稿レポートが膨大な量となっていますが,HPの管理(更新)は1人(早苗先生)に頼り切ってしまっているのが現状で,いままでも私自身のレポートの間違いは何度もあったのでが,早苗先生の手を煩わせることが申し訳なく,「文章全体で概要が分かる」場合については,特に訂正はしませんでした.今回もこのレポートの意図を読み取ってくれればぐらいで考えていたのですが,遠藤先生のご指摘は,その内容はもちろんのことですが,「わたしの点字に対する姿勢の誤り」についてのご指摘でもありました.
「数字「1,2,3,4,5,6,7,8,9,0」と,仮名「あ,い,う,る,ら,え,れ,り,お,ろ」はまったく同じ配列であるから,このままでは視覚障害者は区別をつけることはできない.」
に対して,先生から,
「区別できないのは視覚障害者とは関係ありません」
とのお言葉をいただきました.わたしにとってこのお言葉は,単に誤字・脱字の問題だけではなく,私と視覚障害者のスタンスを思い知らされるご指摘でもありました.私は本レポートを視覚障害者の立場を大事にしながらまとめたつもりなのですが,無意識の中に
「点字を読むのは視覚障害者だけである」
という気持ちがどこかにあったのです.表題についても,表題を点字で表すとこうなるということを示すためにそのパターンを入れたのですが,そこにはまず表題を目で見ることがあり,付録として点字パターンが載せたような興味本位の姿勢があったことは否めないのです.結果,点字という素材を数理的に分析する道具として使ってしまい,石川倉治氏が点字に込めた思いを踏みにじってしまったのです.遠藤先生のお言葉によって,自分の中にある晴眼者と視覚障害者を区別しているその気持ちに気づき,高慢と言葉の怖さを知ることができました.
遠藤先生には,深くお礼申し上げます.


 この3行×2列の枠はマスと呼ばれ,1行1列,2行1列,3行1列をそれぞれ「①の点」,「②の点」,「③の点」という.同様に2列目も上から順に,「④の点」,「⑤の点」,「⑥の点」と表す.そしてこの6つの点の組合せにより,「仮名」,「アルファベット」,「数字」等といった文字が表現される.
この3行×2列の枠はマスと呼ばれ,1行1列,2行1列,3行1列をそれぞれ「①の点」,「②の点」,「③の点」という.同様に2列目も上から順に,「④の点」,「⑤の点」,「⑥の点」と表す.そしてこの6つの点の組合せにより,「仮名」,「アルファベット」,「数字」等といった文字が表現される.
 ⇒
⇒ や
や と区別できない
と区別できない
 ⇒
⇒ と区別できない
と区別できない


 これは,もちろん,3行2列のマスにおいても,右図のように区別はできない.しかし,日常生活においては,点字は,エレベータの上・下の方向,ドアが開く,閉じるといった,固有名詞(単語,自立語ともいう)の認識に重点が置かれるため,横1行のマスの並びでセンテンスは終わる.生活空間を晴眼者と共有するためには,どうしても点字の読解は必要最小限のことを的確に理解することだけに制限されてしまう.したがって,改行する場合はあまり考える必要はないのである.また,点字で長い文章を読み改行がある場合においては,その改行幅を大きくとればいいことになる.だから,3行2列のマスにおいては,横のスペースは,マスとマスを隔てるものであり,縦のスペースは,点と点を隔てるものであると解釈すればよいのだ.
これは,もちろん,3行2列のマスにおいても,右図のように区別はできない.しかし,日常生活においては,点字は,エレベータの上・下の方向,ドアが開く,閉じるといった,固有名詞(単語,自立語ともいう)の認識に重点が置かれるため,横1行のマスの並びでセンテンスは終わる.生活空間を晴眼者と共有するためには,どうしても点字の読解は必要最小限のことを的確に理解することだけに制限されてしまう.したがって,改行する場合はあまり考える必要はないのである.また,点字で長い文章を読み改行がある場合においては,その改行幅を大きくとればいいことになる.だから,3行2列のマスにおいては,横のスペースは,マスとマスを隔てるものであり,縦のスペースは,点と点を隔てるものであると解釈すればよいのだ.

 したがって,6点は,3点+3点に分けるしかないことは明らかである.ただし,3点を縦1列とし,1列,2列で分けると,1列にある3点が表現できる値は2通りしかないわけだから,この分け方では無理である.よって,3点は,
したがって,6点は,3点+3点に分けるしかないことは明らかである.ただし,3点を縦1列とし,1列,2列で分けると,1列にある3点が表現できる値は2通りしかないわけだから,この分け方では無理である.よって,3点は,
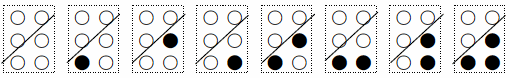




















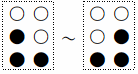









 もう1例をあげると,右の点字はビール缶のタブ(リングプル)近くに打たれているものである.もちろん「ビール」と書いてある.この点字は,いま手に持っている缶がビールという商品を示すということをいっているだけではない.ジュースのような清涼飲料水には点字はついていないので,このビールの点字は,「この商品はジュースではありませんよ」という注意・警告ともとれる.未成年者の誤飲防止といった意味もあるのだろう.
もう1例をあげると,右の点字はビール缶のタブ(リングプル)近くに打たれているものである.もちろん「ビール」と書いてある.この点字は,いま手に持っている缶がビールという商品を示すということをいっているだけではない.ジュースのような清涼飲料水には点字はついていないので,このビールの点字は,「この商品はジュースではありませんよ」という注意・警告ともとれる.未成年者の誤飲防止といった意味もあるのだろう. ちなみに,ビールの缶には右の点字が打たれていることもある.これは何と読むだろうか.
ちなみに,ビールの缶には右の点字が打たれていることもある.これは何と読むだろうか. この後,日本の点字は独自の発展を遂げていき,「6点漢字」,「漢点字」といった漢字の分野にまで進出していくが,その普及と並行して書物を点字に翻訳(点訳)する必要性が生じてくる.点字に対して晴眼者の読む文字を総称して墨字というが,この墨字を点字に書き換えるのは実は大変な作業なのである.墨字を点字に直すには,原稿用紙を点字盤の上に乗せ先端が針状になった点筆と呼ばれる道具で,用紙に垂直に打って窪みをつけていく.これを裏返しにすると点が凸状に膨らんだ点字ができる.だから,点字を書くときには裏返しになることを考え,右から左の方向に,さら「読む点字」に対して鏡面対称に配置された点字を打たなければならない.「読む点字」と「書く点字」は,行方向,点字の配置ともに異なっているのである. 近年は,点字タイプライターやコンピュータソフト(ういんびー)に代表される)による出力も可能になったがそれでもその手間と労力は大変なものといえるだろう.
この後,日本の点字は独自の発展を遂げていき,「6点漢字」,「漢点字」といった漢字の分野にまで進出していくが,その普及と並行して書物を点字に翻訳(点訳)する必要性が生じてくる.点字に対して晴眼者の読む文字を総称して墨字というが,この墨字を点字に書き換えるのは実は大変な作業なのである.墨字を点字に直すには,原稿用紙を点字盤の上に乗せ先端が針状になった点筆と呼ばれる道具で,用紙に垂直に打って窪みをつけていく.これを裏返しにすると点が凸状に膨らんだ点字ができる.だから,点字を書くときには裏返しになることを考え,右から左の方向に,さら「読む点字」に対して鏡面対称に配置された点字を打たなければならない.「読む点字」と「書く点字」は,行方向,点字の配置ともに異なっているのである. 近年は,点字タイプライターやコンピュータソフト(ういんびー)に代表される)による出力も可能になったがそれでもその手間と労力は大変なものといえるだろう. ただ母音に関して,もう一度その配置の順番を見てみよう.母音「あ,い,う,え,お」を点の個数で場合分けして並べていくならば,「え」と「お」だけを並べ替えたらきれいに配置されることに気がつく.この程度の入れ替えはブライエの点字を基にしてもなんら影響はなかったはずだし,その方が視覚障害者にとってもずっと覚えやすいはずなのだ.では,石川氏と点字選定会のメンバーは,なぜこの部分を問題にしなかったのだろうか.
ただ母音に関して,もう一度その配置の順番を見てみよう.母音「あ,い,う,え,お」を点の個数で場合分けして並べていくならば,「え」と「お」だけを並べ替えたらきれいに配置されることに気がつく.この程度の入れ替えはブライエの点字を基にしてもなんら影響はなかったはずだし,その方が視覚障害者にとってもずっと覚えやすいはずなのだ.では,石川氏と点字選定会のメンバーは,なぜこの部分を問題にしなかったのだろうか. 石川倉治氏は,多少の五十音のずれよりも,視覚障害者が「め」を触ったときの感動と安らぎを大切にし,「め」がこの配置になることを何よりも優先したのだろう.
石川倉治氏は,多少の五十音のずれよりも,視覚障害者が「め」を触ったときの感動と安らぎを大切にし,「め」がこの配置になることを何よりも優先したのだろう.