札幌藻岩高校　中村　文則

【材　料】　本時で使用する素材

【下ごしらえ】

【調　理】

《基本編1》　　〜UFOから最大値・最小値をメイクる

• 楕円状に切り抜いた西洋紙の上に鉛筆を置き、包み、これはUFOであることを説明する。
  (UFOに見えないという声が挙がった場合は一喝する)
• 黒板に適当な曲線を描き、UFOを曲線の上空から降下させ、最初に曲線とぶつかった点が、UFOを定義域とみた最大点であることを説明する。
• 曲線の下方よりUFOを上昇させ、最初にぶつかった点が、最小点であることを説明する。

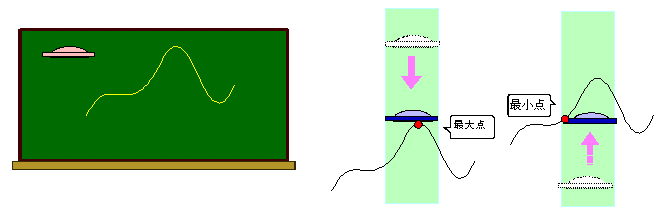
《基本編2》　　〜UFOから二次関数の最大値・最小値をメイクる

• 問題を提示し、そのグラフを描く。

  ex1) 放物線 y=x2-4x+5 (a≦x≦a+1) の最大値・最小値を求めよ。

  

• UFOの右端、左端にそれぞれ、マジックで、a，a+1 と書き、UFOが区間を表していることを説明。
• UFOを x軸に沿って右方向にスライドさせ、放物線の最小点の変化を眼で追わせる。
• 生徒を一人選ぶ。再度、UFOをスライドさせ、最大点が変わった場所(バトンタッチする場所)で、「ストップ」と声をかけて、UFOを停止>させるように指示する。
• 生徒がストップさせた場所が最小点のバトンタッチの点であることを次のように確認する。
  �@UFOをバトンタッチの点より少し左に戻し、上昇させ、最初に放物線とぶつかった点を確認。
  �AUFOをバトンタッチの点より少し右に進め、上昇させ、最初に放物線とぶつかった点を確認。
  �B上で確認させた２つの点が異なっていることを確認させる。
  

• UFOの位置と、放物線との接触地点の高さを記入する(最小値を求める)。
• 次に、最大点について同様の操作をし、バトンタッチの前後において、UFOを下降させて、最初にぶつかった点を確認させ、最大値を求める。
  

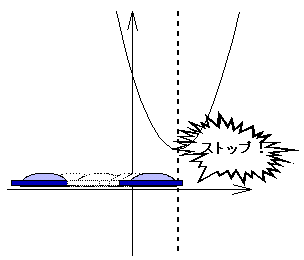
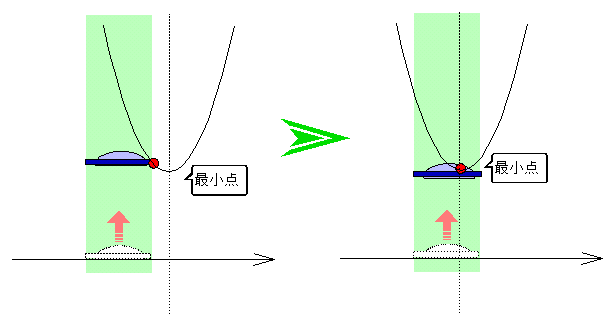
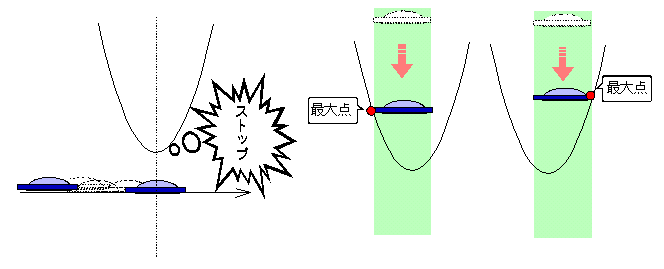
《応用編1》　　〜UFOに乗って最大・最小をメイクる

• ex1の最大点・最小点のバトンタッチ地点を次の手順で調べる。
  �@グラフの左端下方よりUFOを上昇させ、最初にぶつかった点(最小点)で停止させる。
  �A接触した点からグラフをなぞるようにUFOをスライドさせ、接触点(最小点)の変化を読み取る。
  �B最初に接触点が変化する場所のUFOの影を放物線下方に書き込む。
  �C次に接触点が変化する場所のUFOの影を放物線下方に書き込む。
  �Dグラフの左端上方よりUFOを下降させ、最初にぶつかった点(最大点)で停止させる。
  �E以下、最小点の場合と同様に操作をする。
  
• 出来上がった図に、バトンタッチを示す位置(a の値)を書き込む。
  　(真中の影は、上下の a の値の平均を調べればよい)

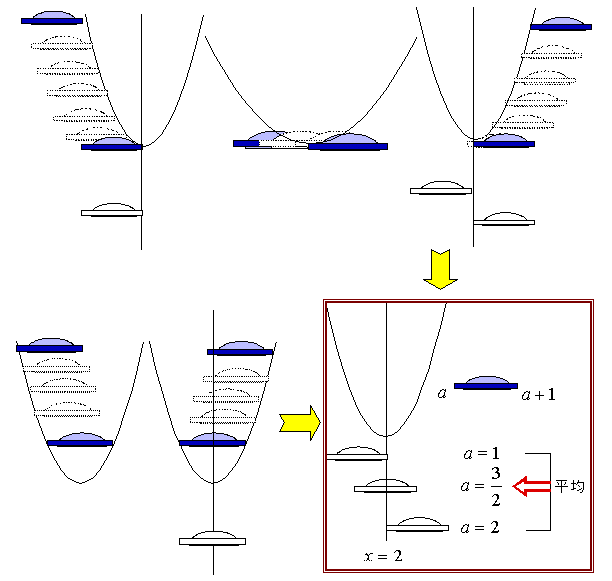
《応用編2》　　〜グラフからUFOを眺めて最大・最小をメイクる

ex2) 放物線 y=-x2+2ax (1≦x≦3) 　の最大値・最小値を求めよ。

• 標準形に変形し、グラフの大まかな概形を押えよう。
  頂点 (a，a²) 、軸の方程式 x=a である上に凸の放物線。
  
• 相対的位置関係についての説明。

  説明例) 　諸君が歩道から道路を走っている車をみるとしよう。車は諸君の横をブーンと通り過ぎ、前方にある橋を突っ切る。だがここで、諸君がその車に乗っていると考えてみよう。このときもちろん車は動いてはいるのだが、意識としては周りの風景が前方から後方に流れているように感じないだろうか。車が橋を渡る場合は、橋が車に近づいて車のヘッドを通り、橋の真中が車を通過し、そして後方に橋が流れ過ぎていく。 　そう考えて、橋を区間、車を放物線とみれば、どちらが動いているかは大した問題ではないことがわかる。区間と放物線の位置関係だけを考えればいいのだ。そこで、UFOを飛ばしてみよう……

• 放物線の頂上(頂点)に立ってみよう。そのとき放物線が動いていると考えずにUFOが放物線に近づいてくる思い込もう。UFOはやがて放物線の山に追突するだろう。UFOが動いているとみても同じなのだ。
  

  

• 最大点・最小点のバトンタッチの地点を確認し、そのときの a の値を求めよう。
• 《応用編1》とバトンタッチの地点が同じになることを確認する。

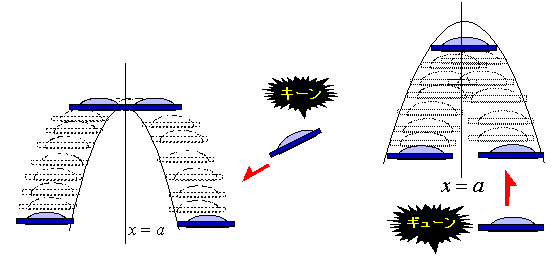
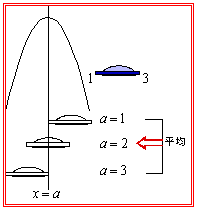
《応用編3》　　〜UFOからビームを発射して最大・最小をメイクる

ex3) 放物線 y=-x2+4x (0≦x≦a) の最大値・最小値を求めよ。

• 放物線を標準形に変形し、頂点、軸の方程式を求め、グラフを描く。
• 区間の右端が延びていく場合の最大・最小であることをゴム紐などを使って確認させる。
• 区間の右端(この場合は 軸上)にUFOを設置する。
• UFOを下降させ、右方向に向かってビームを発射する。
• UFOが頂点の高さまで到達しビームを発射するとき、ビームは頂点にあたることを確認し、この点が最大点のバトンタッチの点であることを説明する。
• ビームの長さと放物線にぶつかった点の位置関係を調べる。
• 次にUFOを下方から上昇させ、ビームを発射し、放物線にぶつける。
• 原点でUFOは放物線とぶつかり、ビームがあたった２点が最小点であることを確認する。

まとめ

　放物線の最大・最小問題は、間違いなくこの単元では最小の理解しか得られない最大の難所である。
　指導を困難にする要因のひとつは「数と式」から始まった基本的計算指導が、グラフ単元で動的、視覚的に転換することへの生徒の戸惑いもあるが、「最大値・最小値」の「値の捉え」にも問題があるのではないかと思う。
　最大値・最小値はもちろん関数の値の最大・最小であるが、その値を判断するためにはまずその「位置」を押さえる必要がある。「最大点・最小点」のことである。しかしこの言葉がなぜか教科書では登場してこない。数�Uにおいても極値の説明はあるが極点は触れられない。場所が特定できてこそ、その高さを調べる価値が生まれるのではないだろうか。そしてそれは理解しているがその言葉を使わない(使えない)指導側と、最大値・最小値だけで、位置の意味も広義に含めてしまっている生徒とのギャップとなってくる。
　　　「最大値はひとつだが、最大となる x の値はひとつとは限らない」
なんて説明は、生徒には
　　　「最大値はひとつだが、最大となる値はひとつとは限らない」
と聞こえていないだろうか。矛盾する表現である。だが、最大点という言葉が使えれば、
　　　「最大値はひとつだが、最大点はひとつとは限らない」
すっきりまとまるのである。
　そこで、今回の「メイクる」では、最大点・最小点の位置をどう視覚的に理解するかを追求してみた。２次関数のグラフでは、最大点・最小点は、区間の両端の関数値、頂点のいずれかに限定されるから、単純にその３点の関数値の大きさを比較すればもちろん求められる。だがこれは、最大点⇒最大値への思考のプロセスを省いた最悪の方法であろう。
　右端点、左端点、頂点を結び、三角形を作り、その３頂点の位置から判断するという方法もある。だが、放物線の頂点は必ずしも範囲に含まれないこともあるわけだから、この方法も限界がある。
　そういった試行錯誤の結果、以前、「小手技シリーズ」のなかで「放物線の最大・最小」を取り上げ、最大・最小のバトンタッチ点を七・五・三シェーマ図として提示したことがある。コンパクトにまとめるにはこの方法がベターであると思うが、ところが最近はこの方法でも理解を得ることが難しくなってきた。
　それは義務教育における数学単元の内容の削減が確実に生徒の能力低下(学力低下ではない、要求学力がそうなのだから、そのレベルでは問題ないということである)を引き起こしたためである。数学を学んだあとの個々人が練る時間の不足は、例えば、イメージ(感覚)として、グラフの変化の様子を創造することができない生徒を激増させた。
　今回の「メイクる」は、そのイメージの不足、欠落を応急的に補うことができないかと考えてみた。
　道具は１本の棒(割り箸、鉛筆、何でもよい)。区間を x軸方向へスライドさせると、生徒はその変化に合わせて値の変化も眼で追おうとする。右端、左端、頂点を同時にである。そこで区間自体を棒と考え、スーッと上下させてみたら、途端、視線の動きもスーッと滑らかになった。生徒の視線は、右端、左端、頂点を追うのではなく、棒の動きを見ているだけになり、グラフとの接触を容易に判断できるようになった。
　ただ、応用編3はちょっと無理があったようだ。UFOだからビームぐらい発射するだろうと思って作ったのだが、ビームの伸び方がいまいち分かり辛いかもしれない。シンプルにゴム紐を伸ばした方がいいようだ。UFOによる方法では、区間変動の場合の方が分かりやすくなってしまったわけだから、不思議なものである。
　なお、応用編1の最大・最小において、UFOの左端点の x座標が a ということから、左端点の軌跡を考えると a を変数とした最大値・最小値のグラフが自然と浮かび上がることになる。これもまたUFOの副産物である。