数学的活動を大切にする
安田 富久一
【発見やイメージを大切にする】
《あみだくじの問題と帰納法》
あみだくじで,必ず違う場所を選ぶと違う場所に出ることの説明で帰納法のイメージを理解させる。
☆ まず,横棒が1本のとき当たり前なことを確認する。
横棒が2本のときは,あみだくじが4種類あることを説明し,確認する。
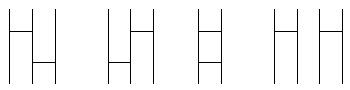 次に横棒が3本になったらどうかを尋ね,生徒の様子を見る。
次に横棒が3本になったらどうかを尋ね,生徒の様子を見る。
「面倒だ」などという声が出て来てもしめたもの。「じゃ,3本の場合,全部確認しなくてもわかるかな」と聞き返せばよい。
そのような言葉が返ってこなければ,「面倒だよね,次4本の場合どうする。やっぱり全部やってみる。なんかうまい方法ないかな。」と言って少し時間をとっても良いし,この段階で,「今,調べたことを利用できないかな」と言いながら,あみだくじの最下段の横棒を黒板から1本消してみるというヒントを与えても良い。
どちらにするか,また別の方法を採るかは,日頃目の前にしている生徒の実態把握に因る。
《注》「異なる2カ所から出発して同一出口に至った場合,あみだくじを逆さまにすると,1カ所から出発して2カ所の出口になることになる。そんな変なことはないよ」という生徒がいたら,率直に誉める。決して,自分が今日やろうとしている方法と違うからと言って,おざなりな誉め方で終わらないように。「んー,先生が考えたのよりいいな」ぐらい誉めて,「でも,折角先生も考えたから先生が考えたのも紹介したいな」と言って進める。ついでに,その方法は「背理法という説明の仕方だったね」と復習をしておく。そして,教科通信にでも,その生徒の名前入りで取り上げると良い。
【不確定のものを根拠に話すことの怖さ:論理】【表現力・コミュニケーション能力】
《自然数の最大値は"1"だ!》
自然数の最大の値をnとする。自然数を2つかけても自然数だからn2も自然数になる。自然数の中でnが一番大きい数だから,n≧n2 である。これを満たすnは,2次不等式を解いて,0≦n≦1。これを満たす自然数nは n=1 ? 。
☆これを生徒に説明し,考えさせる(グループで考えさせるのも面白い)。
生徒の実態に応じて,課題プリントとしても良い。但し,あくまでも正解を出すということよりも,どれだけいろいろなことを考えられるかにポイントをおき,頭に浮かんだことを何でもたくさん書いてくるようにとコメントして課題にする。
【問題が解けたら終わりではない】【一般化】
《ラグランジュの補間》
理科などでは,実験のデータをグラフ用紙に書き入れ,その点を通るグラフを描き,その式を求めたりすることがある。点が3つあれば,2次式が決定するが,それを手始めに,3点を通る2次関数の復習問題を生徒に提示する。
☆その後で,ラグランジュという人がこんなことを考えたと言って,ラグランジュ補間の手法を説明する。
x=aのとき1となり,x=b,cのとき0となる2次式が 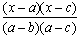 であることを見つけて,これをうまく利用して上記問題を解いた追体験を生徒にさせる(但し,上記のをそのままでするかどうかは,生徒の実態に因る)。
であることを見つけて,これをうまく利用して上記問題を解いた追体験を生徒にさせる(但し,上記のをそのままでするかどうかは,生徒の実態に因る)。
この後,「じゃ,次に皆だったらどんなことを考えてみる」と聞いてみることも大切。
【機械的人間への警告】
盲目的に技能を身につけるだけの生徒への警告として,答えのない問題を出すことも考えられる。
《例》2次関数が,y=ax2+ax+b が,x=1で最大値3をとるように,定数a,bの値を定めよ。
【驚きから興味・関心を引き出す】【教師の思いを伝える】
《どちらが正しい?》
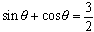 のとき,sinθcosθ の値をA君,B君はそれぞれ次のように解いた。答えが違う。以下の2人の解答を読んで各自思うことを(感想)を述べよ。
のとき,sinθcosθ の値をA君,B君はそれぞれ次のように解いた。答えが違う。以下の2人の解答を読んで各自思うことを(感想)を述べよ。
<A君>
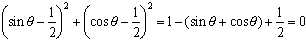 より,
より,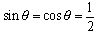 となり,求める値は,
となり,求める値は,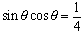 。
。
<B君>
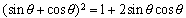 であるから,
であるから,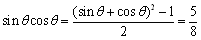 が求める値である。
が求める値である。
☆これも,グループ討議や課題として扱えるが,うまくいけば教師の思いを伝える更に発展した話が可能になる。いわゆる,考えたこと,思ったこと等をレポートするつもりで,この問題に関してどれだけいろいろ考えたり思ったりできるかをポイントにすることを生徒に伝える。
《注》ここでも要注意は,「sinθ+cosθの最大値は√2である。だから,より大きな値である 3/2 にはなり得ず,間違った仮定から出発しているので,どんな結果が出ても不思議ではない」というレポートは,あまりよい評価を与えないこと。
【驚きから興味・関心を引き出す】
《ベルトランのパラドックス:どちらが本当の確率?》
与えられた円に交わる直線を引くとき,その円に内接する正三角形の1辺の長さより も長くなる確率はいくらか。
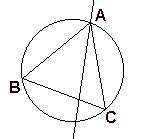 《解1》
《解1》
直線が円と交わった2点のうち片方をAとし,Aを頂点とする円の内接正三角形の残りの頂点をB,Cとする。
このとき,直線と円のもう一方の交点が円弧BCの間にある時に内接正三角形の一辺より長くなる。
円弧BCは円周の3分の1なので,求める確率は。1/3
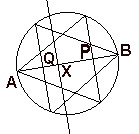 《解2》
《解2》
円と交わる直線に垂直な直径をABとする。点Aを頂点とする円の内接正三角形の点Aの対辺と直径ABとの交点をPとする。また,点Bを頂点とする円の内接正三角形の点Bの対辺と直径ABとの交点をQとする。
円と交わる直線との交点をXとすると,点Xが線分PQに含まれる時に内接正三角形の一辺より長くなる。
線分PQの長さは直径の半分なので,求める確率は 1/2 。
《注》深入りすると数学的に難しい。生徒が混乱を起こさないかどうかの判断が大切。生徒に提示する場合には要注意。
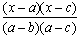 であることを見つけて,これをうまく利用して上記問題を解いた追体験を生徒にさせる(但し,上記のをそのままでするかどうかは,生徒の実態に因る)。
であることを見つけて,これをうまく利用して上記問題を解いた追体験を生徒にさせる(但し,上記のをそのままでするかどうかは,生徒の実態に因る)。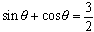 のとき,sinθcosθ の値をA君,B君はそれぞれ次のように解いた。答えが違う。以下の2人の解答を読んで各自思うことを(感想)を述べよ。
のとき,sinθcosθ の値をA君,B君はそれぞれ次のように解いた。答えが違う。以下の2人の解答を読んで各自思うことを(感想)を述べよ。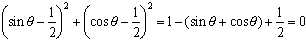 より,
より,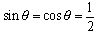 となり,求める値は,
となり,求める値は,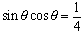 。
。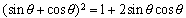 であるから,
であるから,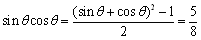 が求める値である。
が求める値である。 《解1》
《解1》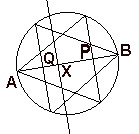 《解2》
《解2》