ベクトルの和( 初歩の初歩について )
札幌稲北高等学校 角田 義一郎はじめに
ベクトルを学ぶ生徒にとって,最初のつまずきは「ベクトルの和」のところです。ベクトルの和
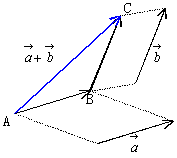 2つのベクトル 2つのベクトル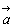 , ,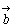 に対してAを始点として に対してAを始点として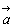 に等しく に等しく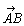 をとり,Bを始点として をとり,Bを始点として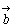 に等し に等し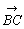 をとる。このとき,Aを始点,Cを終点とするベクトル をとる。このとき,Aを始点,Cを終点とするベクトル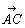 を を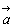 と と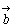 の和といい の和といい
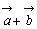
で表す。すなわち
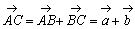
である。 |
これは,「ベクトルの和の定義である」とするも「どうして?」という生徒がいます。
定義が素直に頭に入らず,ここでつまずくと生徒は,なかなかベクトルになじんでくれず「数B」は難しいと思いこみ以後の学習にマイナスになります。
数Bの教科書の「ベクトル」では,矢線ベクトルから始まり,次に成分表示となり,行ベクトルへと進んでいきます。
これを逆に行ベクトルから矢線ベクトルへと進むと「ベクトルの和の定義」が生徒にとって納得しやすくなるのではと思い,まとめてみました。
1.行ベクトル
みかんとりんごそれぞれ1個の値段を10円,20円とする。 これを (10,20) ・・・ ① と表すことにする。
ここでみかんをx個,りんごをy個買ったときの合計金額は
10x+20y (円) である。
一方,10x+20y を2つの文字xとyに関する1次同次式とみなし,最初にxの係数,次にyの係数を書くことにすると ①と同じく
(10,20)
と表すことができる。
同様にみかん,りんご,なしのかんずめがあって,それぞれの値段が1個ずつ200円,100円,300円のとき,これを
(200,100,300) ・・・ ②
と表せる。
また,3つの文字x,y,zに関する1次同次式 2x+y+3zは
(2,1,3) ・・・ ③
と表せる。
①,②,③のように横に並べた数の組のことを行ベクトルとよび,行ベクトルをつくっている個々の数をその成分,成分の個数を次元という。
ここで,行ベクトルを 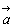 ,
,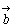 ,
,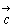 ・・・ で表すことにする。たとえば
・・・ で表すことにする。たとえば
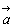 =(10,20),
=(10,20),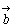 =(200,10,300),
=(200,10,300),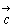 =(2,1,3)
=(2,1,3)
と書く。
行ベクトルの相等
2つの2次元の行ベクトル 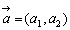 , ,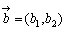 が等しいときはa1=b1,a2=b2となる。 が等しいときはa1=b1,a2=b2となる。 |
よって,2つの行ベクトルが等しいときは,2つの行ベクトルの次元が等しく,かつ対応する成分がすべて等しいことである。
2つの3次元の行ベクトルについても同様に考える。
みかんとりんご1個ずつの値段は (10,20),それぞれのかんずめ1個ずつの値段は (200,100)と表せる。くだものとかんずめをそれぞれ1個ずつ買うと,それぞれの値段は
となる。
これは 2次元の行ベクトル (10+200,20+100) で表され,
(10+200,20+100)=(10,20)+(200,100)
と考えることができる。 一般に 2つの行ベクトル (a1,a2),(b1,b2) について
(a1,a2)+(b1,b2)=(a1+b1,a2+ b2)
が成り立つ。ゆえに
ここで,くだものとかんずめをそれぞれみかんはx個ずつ,りんごはy個買うとくだものとかんずめの合計金額は
| くだもの | かんずめ |
| 10x+20y(円) | 200x+100y(円) |
となる。これを 2つの文字xとyについての1次同次式と考えて加えると
(10x+20y)+(200x+100y)=(10+200)x+(20+100)y ・・・ ④
が成り立つ。 2つの文字x,yに関する1次同次式 10x+20y は (10,20)と表され,
同様にして 200x+100y は (200,100)と表される。
また,(10+200)x+(20+100)y は,(10+200,20+100)となり④から
(10,20)+(200,100)=(10+200,20+100)
は成立する。
以上のことからも
(a1,a2)+(b1,b2)=(a1+b1,a2+ b2)
が成立する。
 2.矢線ベクトル
2.矢線ベクトル
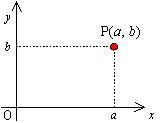
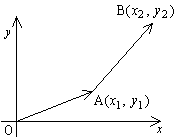
右図においては,平面上の点Pを1組の数(a,b)で表す。 ここで,平面上の点A(x1,y1)を
x2=x1+2,y2=y1+3
で与えられる点B(x2,y2)に移す変換を考える。
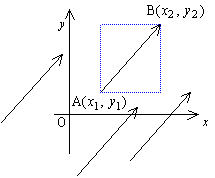 これは図が示すような平行移動である。この平行移動は 点Aが点Bへ移るので有向線分
これは図が示すような平行移動である。この平行移動は 点Aが点Bへ移るので有向線分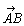 と表すことにする。
と表すことにする。
このように,有向線分で表される量を矢線ベクトルという。平行移動の他に力,速度なども矢線ベクトルである。
いま,有向線分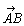 を対角線として,それぞれx軸,y軸に平行な辺をもった長方形を作図すると,点Aを通る辺の長さは,それぞれ2と3である。このことは点Aをどこにとっても成り立つ。
を対角線として,それぞれx軸,y軸に平行な辺をもった長方形を作図すると,点Aを通る辺の長さは,それぞれ2と3である。このことは点Aをどこにとっても成り立つ。
 一般に,点A(x1,y1)を
一般に,点A(x1,y1)を
x2=x1+p,y2=y1+q
で与えられる点B(x2,y2)へ移す平行移動は,矢線ベクトルでは 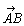 と表されて行ベクトルでは
と表されて行ベクトルでは
(x2-x1,y2-y1)=(p,q)
と表される。
ゆえに 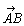 =(p,q) となる。 =(p,q) となる。 |
ここで O(0,0),A(x1,y1)のとき
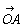 =(x1,y1)
=(x1,y1)
である。
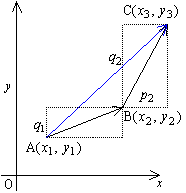 平行移動
平行移動
x2=x1+p1,y2=y1+q1
により点A(x1,y1)は点B(x2,y2)に移り,また,平行移動
x2=x1+p2,y2=y1+q2
によって点B(x2,y2)が 点C(x3,y3)に移されたとする。よって
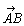 =(p1,q1),
=(p1,q1),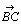 =(p2,q2)
=(p2,q2)
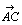 を対角線として,それぞれx軸,y軸に平行な辺をもった長方形を作図すると,点Aを通る辺の長さは,それぞれp1+p2,q1+ q2となる。よって
を対角線として,それぞれx軸,y軸に平行な辺をもった長方形を作図すると,点Aを通る辺の長さは,それぞれp1+p2,q1+ q2となる。よって
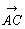 =(p1+p2,q1+q2)
=(p1+p2,q1+q2)
一方 (p1+p2,q1+q2)=(p1,q1)+(p2,q2)
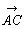 =
=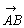 +
+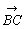
ゆえに
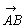 +
+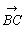 =
=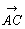
が成り立つ。
3.ベクトルの初歩「和の定義」
ベクトルの導入として,行ベクトルから矢線ベクトルへと進み,和の定義を平行移動をイメージさせて説明すると,生徒もわかってくれたようでした。
ベクトルの基本となる「和の定義」を論理的に導くことにより,生徒もベクトルの食わず嫌いにおちいることなく以後の授業もわりとスムーズに進めることができました。 みかんとりんごそれぞれ1個の値段を15円,25円とする。
これを (15,25)・・・⑤ と表すことにする。 ここでみかんをx個,りんごをy個買ったときの合計金額は
15x+25y・・・⑥(円)である。
15x+25y=(15,25)・(x,y) と書くことにする。
よって (15,25)・(x,y)=15x+25y となり,内積を導くことができる。
ただし,まだ生徒には,このだんかいでは「内積」は,教えないことにします。
ここで この合計金額を内積としてしまうと,2つのベクトルのなす角を教えたときに「(15,25)と(x,y)のなす角ってなんですか」と無意味な疑問をもってしまう生徒がいるからです。
第27回「数実研」で北海道石狩南高校の清水貞人先生が,発表されたレポート「ベクトルの内積の導入について」を,数学のいずみ(数実研のホームページ)で読んだ大阪の灘高校2年生が,数学のいずみの意見欄にメールを送ってきました。
その中に「清水先生は,授業例として値段ベクトル,個数ベクトルを用いていますが・・・・値段ベクトルと個数ベクトルのなす角って何ですか?と質問されれば,困ってしまうのではないでしょうか」とありました。
このことについて清水先生は,高校生に送ったメールの中で「・・・ベクトルの内積を数ベクトルで定義することについて・・・授業をするときは,十分配慮しなければならないと思っています」と答えています。
このあたりのことについてもっと詳しく知りたい方は,「数学のいずみ:あなたの意見のまとめ」を開くとよいでしょう。
上の式を内積の定義としても生徒は,理解しずらいと思います。
それは以下のようなことからです。
実数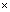 実数=実数, 複素数
実数=実数, 複素数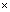 複素数=複素数 であるが,ベクトルのスカラー積はベクトルにならないので,スカラー積はふつうの意味の積ではない。
複素数=複素数 であるが,ベクトルのスカラー積はベクトルにならないので,スカラー積はふつうの意味の積ではない。
しかし,ふつうの積に似た性質(1)(2)(3)があるため,便宜上積とよぶ。
| 交換法則 | 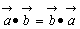 | (1) |
| 分配法則 | 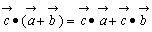 | (2) |
| 結合法則 | 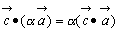 ただしαは実数 ただしαは実数 | (3) |
スカラー積のことを,内積(inner product)という。
内積を導入するには,矢線ベクトルを使い図形のイメージから入ると,生徒も理解しやすいと思います。
4. 内積の導入 ( 図形のイメージから入る )
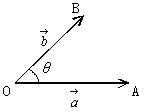 余弦定理から
余弦定理から 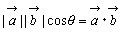 へと進む。
へと進む。 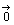 でない2つのベクトル
でない2つのベクトル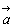 ,
,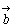 に対して,点Oを定め
に対して,点Oを定め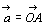 ,
,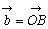 であるように点A,Bをとる。
であるように点A,Bをとる。
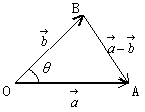 このとき∠AOBの大きさθを
このとき∠AOBの大きさθを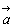 ,
,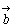 のなす角という。ただし0°≦θ≦180°とする。
のなす角という。ただし0°≦θ≦180°とする。
△OABにおいては,余弦定理により
BA2=OA2+OB2-2OA×OB×cosθ
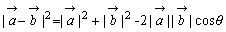 ・・・ ①
・・・ ①
これはθが0°または180°のときも成り立つ。
このように,2つのベクトル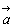 ,
,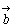 に対して
に対して 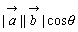 を考えることは図形的にも意味がある。
を考えることは図形的にも意味がある。
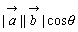 を,
を,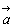 と
と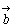 の内積といい 記号で
の内積といい 記号で 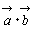 と表す。
と表す。
* 考察 余弦定理から 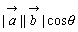 を導くと,図形的なイメージがあるので内積がわりとスムーズに導入できる。
を導くと,図形的なイメージがあるので内積がわりとスムーズに導入できる。
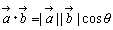
また 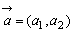 ,
,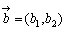 のとき①は
のとき①は
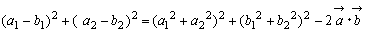
と表されるので 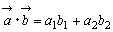
内積のイメージ化(生徒に対して)
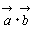 は
は 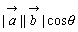 を表す記号であることを力説してイメージとして2辺きょう角がうかぶよにさせる。
を表す記号であることを力説してイメージとして2辺きょう角がうかぶよにさせる。
2辺きょう角のイメージ化
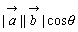 は, は,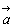 と と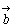 の内積である。記号で の内積である。記号で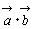 と表す。 と表す。
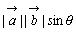 は,平行四辺形の面積である。面積は記号で は,平行四辺形の面積である。面積は記号で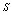 と表す。 と表す。 |
5.ベクトル積について
2つのベクトル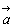 ,
,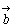 によってつくられる平行四辺形の面積を,この面に直角の方向をもったベクトル
によってつくられる平行四辺形の面積を,この面に直角の方向をもったベクトル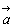 ,
,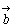 のベクトル積といい,
のベクトル積といい,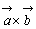 で表す。
で表す。
ベクトル積のことを外積(outer product)という。べクトル積の大きさは,2つのベクトルのなす角がθのとき
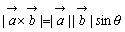
とする。ただし,その向きは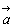 から
から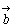 へ180°の角度でまわるとき右ねじの進む向きとする。
へ180°の角度でまわるとき右ねじの進む向きとする。
6.内積の導入・・・その2 (唐突な感じ)
2つのベクトル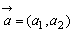 ,
,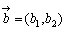 に対して,
に対して, 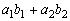 を
を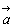 と
と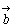 の内積といい,記号で
の内積といい,記号で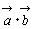 と書く。
と書く。
(生徒にとっては「??」でわからない) これを内積の定義とする導入方法は,唐突な感じうけ生徒にとってはチンプンカンプンと思われる。・・・以下次のように続く。
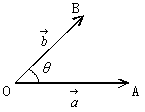 ・ベクトルのなす角
・ベクトルのなす角
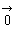 でない2つのベクトル
でない2つのベクトル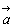 ,
,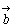 に対して1点Oを定め,
に対して1点Oを定め,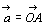 ,
,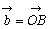 である点A,Bをとる。このとき,∠AOBの大きさθを
である点A,Bをとる。このとき,∠AOBの大きさθを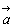 ,
,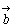 のなす角という。ただし,0°≦θ≦180°。
のなす角という。ただし,0°≦θ≦180°。
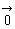 でない2つのベクトル
でない2つのベクトル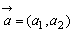 ,
,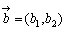 に対し,2点A(a1,b1),B(a2,b2)をとれば,
に対し,2点A(a1,b1),B(a2,b2)をとれば,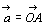 ,
,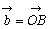 である。
である。
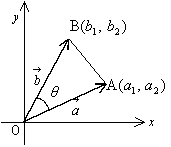
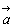 ,
,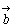 のなす角が0°≦θ≦180°のとき,△OABに余弦定理を適用すると,
のなす角が0°≦θ≦180°のとき,△OABに余弦定理を適用すると,
AB2=OA2+OB2-2OA・OB・cosθ
ここで 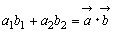 ,
,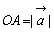 ,
,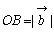 である。
である。
7.最後に・・・まとめとして
今回のレポートは,ベクトルの初歩の初歩として「和の定義」を生徒にわかりやすく指導するには,どうしたらよいかについてまとめてみました。
数Bの教科書は,矢線ベクトルから成分表示へと進んでいきます(平11年度の教科書を,10冊調べてみました)。私の見た限りでは,行ベクトルから矢線ベクトルへ・・・と進む教科書は見あたりませんでした。もし,ありましたら教えていただきたいのですが。
学習指導要領,教科書検定の関係から,矢線ベクトルから入らなければならないのかもしれませんが。 教科書では,矢線ベクトルという語も行ベクトルという語も出てきません。
どちらもベクトルですが,生徒にとっては矢線ベクトルが理解できて無いうちに成分表示に進むと,以後の学習にマイナスとなりベクトルアレルギーにおちいります。
ベクトルの基本をしっかり生徒にわかってもらいたく「和の定義」を行ベクトルから矢線ベクトルへと・・・ しました。
行ベクトル=矢線ベクトルが理解できると,生徒にとって苦手な内積もわかってくれると思います。
行ベクトルと行ベクトルのなす角もイメージできるようになるでしょう。
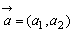 ,
,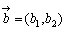 のなす角は
のなす角は 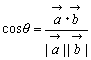 により求まります。
により求まります。
 2つのベクトル
2つのベクトル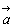 ,
,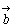 に対してAを始点として
に対してAを始点として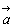 に等しく
に等しく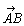 をとり,Bを始点として
をとり,Bを始点として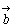 に等し
に等し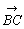 をとる。このとき,Aを始点,Cを終点とするベクトル
をとる。このとき,Aを始点,Cを終点とするベクトル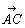 を
を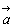 と
と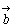 の和といい
の和といい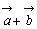
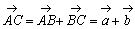
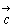 ・・・ で表すことにする。たとえば
・・・ で表すことにする。たとえば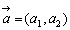 ,
,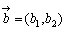 が等しいときはa1=b1,a2=b2となる。
が等しいときはa1=b1,a2=b2となる。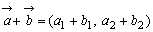
 2.矢線ベクトル
2.矢線ベクトル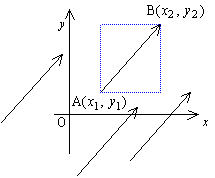 これは図が示すような平行移動である。この平行移動は 点Aが点Bへ移るので有向線分
これは図が示すような平行移動である。この平行移動は 点Aが点Bへ移るので有向線分 一般に,点A(x1,y1)を
一般に,点A(x1,y1)を 平行移動
平行移動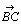 =(p2,q2)
=(p2,q2)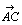 を対角線として,それぞれx軸,y軸に平行な辺をもった長方形を作図すると,点Aを通る辺の長さは,それぞれp1+p2,q1+ q2となる。よって
を対角線として,それぞれx軸,y軸に平行な辺をもった長方形を作図すると,点Aを通る辺の長さは,それぞれp1+p2,q1+ q2となる。よって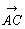 =(p1+p2,q1+q2)
=(p1+p2,q1+q2)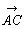 =
=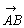 +
+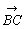
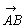 +
+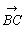 =
=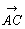
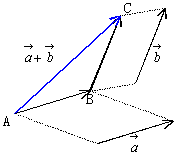 2つのベクトル
2つのベクトル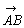 をとり,Bを始点として
をとり,Bを始点として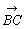 をとる。このとき,
をとる。このとき,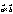 を始点,
を始点,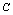 を終点とするベクトル
を終点とするベクトル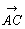 を
を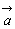 と
と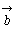 の和といい
の和といい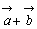
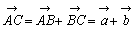
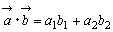
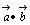 の代数的表示
の代数的表示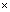 実数=実数, 複素数
実数=実数, 複素数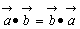
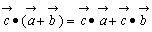
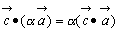 ただしαは実数
ただしαは実数 余弦定理から
余弦定理から 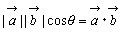 へと進む。
へと進む。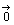 でない2つのベクトル
でない2つのベクトル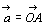 ,
,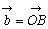 であるように点A,Bをとる。
であるように点A,Bをとる。 このとき∠AOBの大きさθを
このとき∠AOBの大きさθを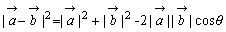 ・・・ ①
・・・ ①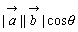 を考えることは図形的にも意味がある。
を考えることは図形的にも意味がある。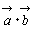 と表す。
と表す。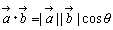
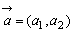 ,
,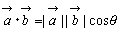
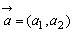 ,
,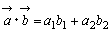
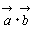 は
は 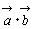 と表す。
と表す。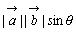 は,平行四辺形の面積である。面積は記号で
は,平行四辺形の面積である。面積は記号で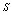 と表す。
と表す。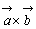 で表す。
で表す。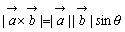
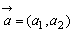 ,
,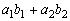 を
を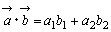
 ・ベクトルのなす角
・ベクトルのなす角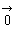 でない2つのベクトル
でない2つのベクトル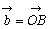 である点A,Bをとる。このとき,∠AOBの大きさθを
である点A,Bをとる。このとき,∠AOBの大きさθを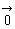 でない2つのベクトル
でない2つのベクトル
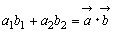 ,
,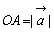 ,
,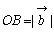 である。
である。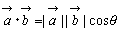
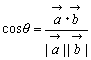 により求まります。
により求まります。