平成10年度2年生の「数学B」を3年ぶりに担当して4か月経ちました。
新学期は「第1章 ベクトル」から授業を開始。ベクトルの「内積の定義」が,生徒にとっては難しく感じられ「定義」がスーッと頭に入っていかないようでした。
生徒にとって「内積の定義」をわかりやすく導入するには,どうしたらよいかその方法を考えてみました。来年(平成11年)度の「数学B」の教科書を10冊参考にしました。
- 数学B (知研出版)
- 改訂版 数学B (数研出版)
- 新数学B (第一学習社)
- 新編 数学B (文英堂)
- 新版 数学B (実教出版)
- 新編 数学B (東京書籍)
- 数学B (東京書籍)
- 数学B [改訂版] (旺文社)
- 探求 数学B (数研出版)
- 新編 数学B (第一学習社)
2つのベクトル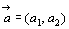 ,
,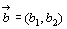 に対して
に対して 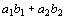 を
を と
と の内積といい記号で
の内積といい記号で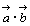 と書く。
と書く。
内積の定義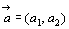 , ,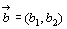 のとき のとき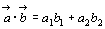 |
これを内積の定義とする導入方法は,唐突な感じをうけ生徒にとってチンプンカンプンと思われる。・・・以下次のように続く。
・ベクトルのなす角
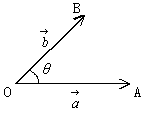
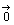 でない2つのベクトル
でない2つのベクトル ,
, に対して1点Oを定め,
に対して1点Oを定め,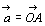 ,
,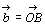 である点A,Bをとる。このとき∠AOBの大きさθを
である点A,Bをとる。このとき∠AOBの大きさθを ,
, のなす角という。ただし,0°≦θ≦180°
のなす角という。ただし,0°≦θ≦180°
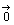 でない2つのベクトル
でない2つのベクトル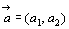 ,
,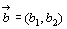 に対し,2点A(a1,a2),B(b1,b2)をとれば,
に対し,2点A(a1,a2),B(b1,b2)をとれば,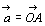 ,
,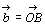 である。
である。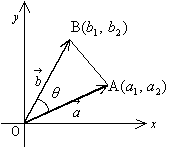
 ,
, のなす角が0°≦θ≦180°のとき△OABに余弦定理を適用すると
のなす角が0°≦θ≦180°のとき△OABに余弦定理を適用すると
AB2=OA2+OB2-2OA×OB cosθ
(b1-a1)2+(b2-a2)2=(a12+a22)+(b12+b22)-2OA・OBcosθ
-2(a1b1+a2b2)=-2OA・OBcosθ
ここで 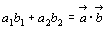 ,OA=
,OA=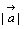 ,OB=
,OB=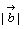 である。
である。
ベクトルの内積 と と のなす角をθとすると のなす角をθとすると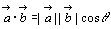 |

 でない2つのベクトル
でない2つのベクトル ,
, に対して1点Oを定め,
に対して1点Oを定め,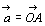 ,
,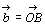 とする。
とする。
このとき∠AOB=θを  ,
, のなす角という。ただし0°≦θ≦180°
のなす角という。ただし0°≦θ≦180°
このとき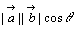 を,
を, と
と の内積といい,記号
の内積といい,記号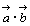 で表す。
で表す。
内積の定義 と と のなす角をθとすると のなす角をθとすると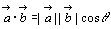 |
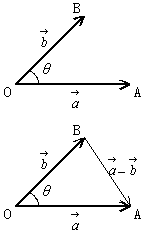
・内積の成分表示
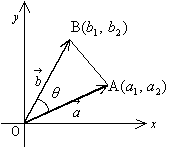
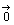 でない2つのベクトル
でない2つのベクトル ,
, を
を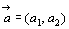 ,
,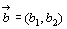 とし,原点Oを始点として,
とし,原点Oを始点として,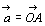 ,
,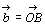 である点A,Bをとる。
である点A,Bをとる。
 ,
, のなす角をθとすると
のなす角をθとすると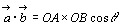
△OABに余弦定理を用いると AB2=OA2+OB2-2OA×OB cosθ
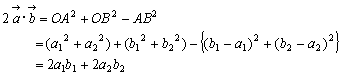
ゆえに 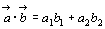
この等式は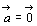 または
または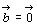 のときも成立。
のときも成立。
内積と成分 と と のなす角をθとすると のなす角をθとすると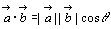 |
 余弦定理から
余弦定理から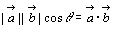 へと進む。
へと進む。
 でない2つのベクトル
でない2つのベクトル ,
, に対して,点Oを定め
に対して,点Oを定め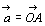 ,
,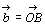 であるように点A,Bをとる。
であるように点A,Bをとる。
このとき∠AOBの大きさθを ,
, のなす角という。ただし 0°≦θ≦180°とする。
のなす角という。ただし 0°≦θ≦180°とする。
△OABにおいては,余弦定理により BA2=OA2+OB2-2OA×OB cosθ
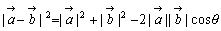 ・・・ ①
・・・ ①
これは θが0°または180°のときも成り立つ。
このように,2つのベクトル ,
, に対して
に対して 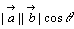 を考えることは図形的にも意味がある。
を考えることは図形的にも意味がある。 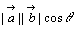 を,
を, と
と の内積といい 記号で
の内積といい 記号で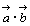 と表す。
と表す。
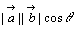 を導くと,図形的なイメージがあるので内積がわりとスムーズに導入できる。
を導くと,図形的なイメージがあるので内積がわりとスムーズに導入できる。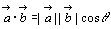
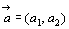 ,
,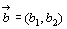 のとき①は
のとき①は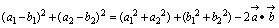
と表されるので
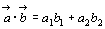
| ベクトルの内積 定義1. 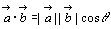 定義2. 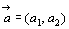 , ,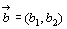 のとき のとき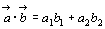 |
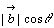 を
を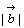 の
の 上への正射影として扱う。
上への正射影として扱う。
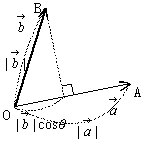 2つのベクトルについて,加法・減法以外の演算を考えてみよう。
2つのベクトルについて,加法・減法以外の演算を考えてみよう。
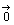 でない2つのベクトル
でない2つのベクトル ,
, について1点Oを定めて
について1点Oを定めて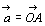 ,
,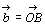 とするとき∠AOB=θを
とするとき∠AOB=θを ,
,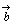 のなす角という。ただし 0°≦θ≦180°
のなす角という。ただし 0°≦θ≦180°
このとき 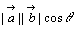 を
を と
と の内積といい
の内積といい 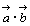 と表す。
と表す。
内積の定義 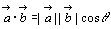 |
内積の定義から内積と成分へは,導入その2と同様な形式で進む。
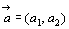 , ,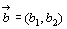 のとき のとき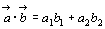 |
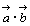 は
は 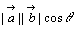 を表す記号であることを力説してイメージとして2辺きょう角がうかぶようにさせる。
を表す記号であることを力説してイメージとして2辺きょう角がうかぶようにさせる。
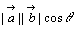 は, は, と と の内積である。記号で の内積である。記号で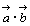 と表す。 と表す。 |
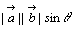 は,平行四辺形の面積である。面積は記号でSと表す。 は,平行四辺形の面積である。面積は記号でSと表す。 |
スカラー積のことを,内積(inner product)という。
 , , の大きさを の大きさを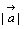 , ,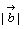 , , と と のなす角をθとするとき のなす角をθとするとき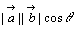 で表されるスカラー量(実数)をベクトル で表されるスカラー量(実数)をベクトル と と のスカラー積といい, のスカラー積といい,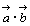 で表わす。 で表わす。 |
スカラー積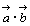 の代数的表示 の代数的表示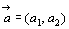 , ,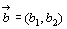 のとき のとき 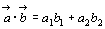 |
実数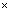 実数=実数, 複素数
実数=実数, 複素数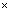 複素数=複素数 であるが,ベクトルのスカラー積は ベクトルにならないので,スカラー積はふつうの意味の積ではない。
複素数=複素数 であるが,ベクトルのスカラー積は ベクトルにならないので,スカラー積はふつうの意味の積ではない。
しかし,ふつうの積に似た性質(1)(2)(3)があるため,便宜上積とよぶ。
交換法則 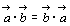 (1)
(1)
分配法則 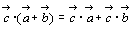 (2)
(2)
結合法則 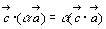 ただしαは実数 (3)
ただしαは実数 (3)
2つのベクトル ,
, によってつくられる平行四辺形の面積を,この面に直角の方向をもったベクトル
によってつくられる平行四辺形の面積を,この面に直角の方向をもったベクトル ,
, のベクトル積といい,
のベクトル積といい,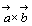 で表す。
で表す。
ベクトル積のことを外積(outer product)という。
べクトル積の大きさは,2つのベクトルのなす角がθのとき
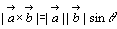
とする。ただし,その向きは から
から へ180°の角度でまわるとき右ねじの進む向きとする。
へ180°の角度でまわるとき右ねじの進む向きとする。