数学問題解答ソフト『MathCalc』が完成するまで

2000.9.22（2002.10.10改定）
北海道滝川工業高等学校
畑　　　仁

はじめに

　数式処理ソフトといえば、『Mathematica』(Wolfram Research社)があまりにも有名だが、価格がProffessional日本語版で226,000円(High-school版は49,000円だが、日本語マニュアルや取り扱い説明書が同梱されず、ヘルプブラウザによって確認しなければならないらしい)と、少々高価なソフトウェアである。
　また、あまりにも多機能すぎることや一回一回コマンドを入力しなければならないことは、WindowsのGUI(Graphical User Interface)環境に慣れきってしまった私にとって、少々使いづらいソフトのように思えてならない。
　であれば、「自分が使いやすいようなソフトを作ってしまおう！」というのが、『MathCalc』を作ろうと思った理由である。今から7年前のことである。その頃のパソコンのOS(Operating System)は、MS-DOSが主流で、当然初期バージョンである『MathCalc Ver1.00』もMS-DOS上で動作するソフトであった。機能も整式の四則演算と因数分解、2次方程式くらいを解く程度で、これから紹介する『MathCalc』の機能の半分程度しかなかった。
　パソコンが普及するにつれ、その技術も発展し、OSもMS-DOSからWindowsへ徐々に移行して、現在では「MS-DOSって何？」というパソコンユーザーも多くなってきた。私のパソコン環境もWindowsに変わり、「MathCalcもWindows版にしたいなぁ」と思うようになった。
　今回の研究発表では、『MathCalc Ver2.00』(以下MathCalcと記述)の機能の説明と、そのアルゴリズムやデータ構造を紹介し、Windows版に移植するにあたっての苦労談を発表しようと思う。また、現在開発中のソフト『Math T_EX』の内容についても触れてみたい。




MathCalcの機能

　MathCalcには、以下の計算を行う機能がある。いずれについても、係数は分数に対応しており、当然答えも分数で表示される。MathCalcを起動すると図1のような画面が現われ、それぞれのボタンを押すことによって、図2 〜4のような画面が現われ、計算することになる。
1. 整式の四則演算
   
   • f(x) + g(x)
   • f(x) - g(x)
   • f(x) × g(x)
   • f(x) ÷ g(x)
   • f(x)^g(x) (ただし、g(x)は定数項)
   • f(x) に g(x) を代入する
   • f(x) と g(x) の最大公約数
   • f(x) と g(x) の最小公倍数
   

   図1：MAthCalcを起動すると

2. 整式の因数分解
3. 連立方程式(2元1次方程式)
4. 2次方程式
5. 高次方程式(4次方程式まで)
6. 内分・外分
   • 内分点の座標
   • 外分点の座標
   • 2点を通る直線の方程式
7. 微分(有理整関数のみ)
   • 微分係数
   • 接線の方程式
   • 極値(3次関数のみ)
8. 定積分(有理整関数のみ)


図2：四則演算のボタンを押すと

　また、係数などを入力するにあたり、Enterキーを押すことによって次の係数の欄にカーソルを移動することができる。さらに、必要な数値が入力されれば、「計算」ボタンをクリックしなくても、Enterキーを押すだけで答えが表示される。



図3：因数分解のボタンを押すと



図4：定積分のボタンを押すと




MathCalcのデータ構造とアルゴリズム

3.1　開発環境

　MathCalcは、Object Pascalで記述されており、『Delphi』(Inprise社)で処理されている。コンパイラにDelphiを選んだ理由は、『MathCalcVer1.00』がPascalという言語で書かれてあったからで、それが発展したObject PascalのWindows版コンパイラだったからである。
　知っての通り、プログラミング言語には、BASICを始め、Fortran、COBOL、C、LISP、Prolog、Ada、Javaなど、数え切れないほどあるが、学生時代よく使っていた言語であるということと、当時構造化プログラミング⁽¹⁾もので、goto文を使わないので、すっきりした読みやすいプログラムを書くことができる。}ができる言語は、PascalかCしかなかったからである。
　ここで、どちらかといえばマイナーな感じを受けるPascalのことについて、若干説明を加えたい。
　Pascalは、Turich工科大学のN.Wirth教授がAlgolの後継者として開発した言語で、一般的にはプログラミング教育のために用いられることが多い。しかし、市販されている(いた)コンパイラ『TURBO Pascal』(Borland社)は多くの拡張が加えられており、C言語ほど低級な記述はできないものの、アマチュアプログラマーが、ちょっとしたソフトウェアを作るには十分過ぎる機能を持つものである。
　言語仕様についての詳細は割愛するが、C言語のそれと似通っているところがある。たとえば、プログラムの始まりと終わりを表す begin … end は、Cでいう { … }であるし、if 式 then … else … ; は、Cでいう if (式) … ; else … ; である。 その他の違いについて、いくつかの例を表にのせた。

	Pascal	C
変数の宣言	var Data:Integer;	int Data;
代入文	a:=1;	a=1;
while文	While (式) do begin … end;	While (式)} { … }
for文	for i:=1 to 10 do begin … end;	for (i=1; i<=10; i++) { … }
論理演算子	and	&&
関数	function abc(a:Integer):Integer;	int abc(int a)
手続き	procedure abc(a:Integer);	void abc(int a)

(1) すべてのロジックを、順次、選択(if文)、繰り返し(while文)の3つのフローチャートの組み合わせによって処理することができる

3.2　データ構造

　特に、プログラムの中で、整式や分数がどう表されているかというと、

Pol=Record
  Degree:Integer;
  Up,Down:array[0..Max] of Integer; 
end;

という風に構造体を用いて、それをPol型と定義した。Degreeはその整式の次数、Upは係数の分子、Downは係数の分母を意味し、それぞれ係数は0次からMax次までの配列となって表されている。なお、整式の最大次数はMax(10に設定)としている。
　ちなみに、C言語風に書くと、

struct Pol{
  int Degree;
  int Up[Max];
  int Down[Max];
};

　また、Basic風に書くと


Type Pol
  Degree As Integer
  Dim Up(Max) As Integer 
  Dim Down(Max) As Integer 
End Type

となる。

3.3　アルゴリズム

　まず、Pol型変数にかかわり、以下の関数及び手続きを作成した。

{最大公約数を求める}
function Gcd(A,B:Integer):Integer;

{最小公倍数を求める}
function Lcm(A,B:Integer):Integer;

{Pol型変数を初期化する}
procedure ClearPol(var A:Pol);

{係数を約分し、次数の適正な値にする}
procedure ReducePol(var A:Pol);

{整数型をPol型0次式に変換する}
function IntToPol(N:Integer):Pol;

{Pol型0次式を整数型に変換する}
function PolToInt(A:Pol):Integer;

{式が 0 かどうか判定する}
function ZeroPol(A:Pol):Boolean;

{式が 1 かどうか判定する}
function OnePol(A:Pol):Boolean;

{式が x かどうか判定する}
function XPol(A:Pol):Boolean;

{同じ式かどうか判定する}
function EqPol(A,B:Pol):Boolean;

{式同士を加算する}
procedure AddPol(A,B:Pol; var C:Pol);

{式同士を減算する}
procedure SubPol(A,B:Pol; var C:Pol);

{式同士を乗算する}
procedure MulPol(A,B:Pol; var C:Pol);

{式同士を除算する}
procedure DivPol(A,B:Pol; var Q,R:Pol);

{式を微分する}
procedure DifPol(A:Pol; var C:Pol);

{式を積分する}
procedure IntPol(A:Pol; var C:Pol);

{式をべき乗する}
procedure PowerPol(A,B:Pol; var C:Pol);

{式に値を代入する}
procedure EnterPol(A,B:Pol; var C:Pol);

{式同士の最大公約数を求める}
procedure GcdPol(A,B:Pol; var C:Pol);

{式同士の最小公倍数を求める}
procedure LcmPol(A,B:Pol; var C:Pol);

{式を文字列に変換する}
function PolToString(var A:Pol):String;

{有理数文字列をPol型に変換する}
function RatStringToPol(S:String):Pol;

　これらを基本関数とし、それぞれの問題に応じた関数や手続きを組み合わせ、計算処理をした。たとえば、比較的処理が簡単だった定積分を例にとれば、以下のような流れ図で処理を行っている。

1. RatStringToPol(S)により、各係数、上端、下端を読み込む。
2. 各係数を元に、Pol型変数Aを作る。
3. IntPol(A,C)により、Aを積分し、Cとする。
4. EnterPol(C,TPol,C1)により、Cに上端(TPol)を代入し、C1とする。
5. EnterPol(C,UPol,C2)により、Cに下端(UPol)を代入し、C2とする。
6. SubPol(C1,C2,Ans)により、C1-C2を計算し、解答とする。

3.4　Windowsプログラミングの考え方

　従来の、MS-DOS上のプログラムは、メインルーチンがあり、そこに主たるプログラムを記述し、キーの入力などに応じてサブルーチンを呼び出し、処理を行っていく考え方であった。
　しかし、Windowsの普及からGUI環境に移行し、操作方法も複雑化していった。たとえば、「ボタンをクリックする」、「メニューを押す」、「キーを押す」、「右クリックする」、「左クリックする」などがそうである。また、Windows独自の現象(「Windowが開く」、「Windowが閉じる」、「Windowの大きさを変える」など)も起こってくる。
　従来のプログラミング技術でも対応できないことはないだろうが、コードは複雑化極まりなくなることは、容易に想像できるだろうし、私のような素人にはとても対応しきれるものではない。
　そこで登場したのが、Delphiのような、イベント駆動(Event Driven)の考え方が盛り込まれたコンパイラ⁽²⁾ である。イベント駆動というのは、何らかのイベント(たとえば、ボタンをクリックする、など)が発生した時に、それに応じた一定の処理手順(たとえば、新たなWindowが開く、など)を実行するというプログラム概念で、イベント単位で個別にプログラムを作り、全体としてうまく動作するようにプログラムを組み立てていくものである。
　また、オブジェクト指向の考え方から、Delphiには、フォームやコンポーネントという形で、たくさんのオブジェクトがすでに宣言されており、私たちは、それらをフォーム上にマウスを使って貼り付けるだけで、基本的なWindowsの機能を持ったフォームを作成できる。さらに、各コンポーネントのプロパティを変更することによって、市販されているソフトのようなフォームを作成することも可能である。
　また、多くのコンポーネントは、WindowsのAPI(Application Programming Interface)をクラスライブラリとして持っており、簡単なプログラムによって、それらを呼び出すことができる。
　たとえば、ファイルを開くときによく目にする図5は、フォーム上にOpenDialogコンポーネントを貼り付け、



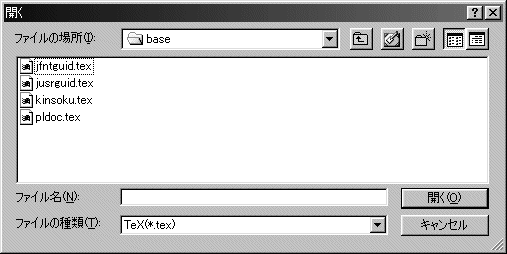
図5：OpenDialog使用例




procedure TForm1.OpenButtonClick(Sender: TObject);
begin
  with OpenDialog1 do begin
    Filter:='TeX(*.tex)|*.tex|All(*.*)|*.*';
    if Execute=True then begin
      Memo1.Lines.LoadFromFile(FileName);
      FFileName:=FileName;
    end;
  end;
end;

と記述するだけで、ファイルを選択し、読み込むことができる。同様に、ファイルのセーブやフォントの変更(図 6)、プリンターの設定なども、簡単なプログラムの記述により実行することができる。このように、現在のWindowsコンパイラは、すでにたくさんのコンポーネントが組み込まれており、私たちは、それらをフォーム上に配置・デザインすることからプログラミングを始めることになる。また、アイコンの作成、ビットマップボタンの設計などの点からも、これからのプログラミングは、美術的なセンスも必要になってくると思われる。


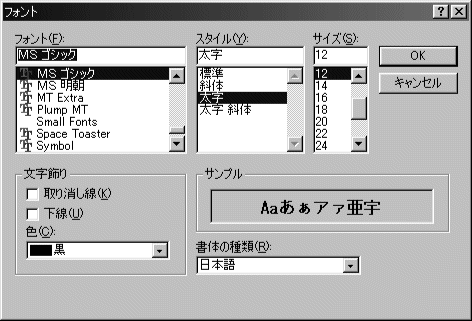
図6：FontDialog使用例




procedure TForm1.FontMenuClick(Sender: TObject);
begin
  FontDialog1.Options:=[fdEffects];
  FontDialog1.Font:=Label1.Font;
  if FontDialog1.Execute then begin
    Label1.Font:=FontDialog1.Font;
    Label1.Font.Style:=FontDialog1.Style;
    Label1.Font.Size:=FontDialog1.Size;
  end;
end;

(2)Visual BasicやVisual C++などもそう
(3)マウスの操作によってWindowの大きさが変わる、ボタンが押されたような動作をする、メニューがドロップダウンする、など
(4)大きさや色、メニューの内容など、各コンポーネントの細部を定義するもの
(5)ビットマップのイメージを表示できるボタン




今後のこと

4.1　MathCalcの機能拡張

　現在のところ、以下の機能拡張を計画中である。

• ユーザーインターフェイスの改善
• 連立方程式での、3元1次や4元1次への対応
• 微分での、4次関数の極値への対応
• �狽ﾌ計算
• n! 、_nP_r 、_nC_r の多桁計算

　機能拡張が出来次第、随時「Vector」(http://www.vector.co.jp/)にアップロードする予定であり、MathCalcを始め私の拙作は、
　　　http://www.vector.co.jp/vpack/browse/person/an008927.html
に登録されているので、ダウンロードし、使用していただければ幸いである。

4.2　MathTeX について

　MathCalcと平行して、MathT_EX というものを開発中である。これは、数学の基本的な計算問題(多項式の四則演算、因数分解、2次方程式、連立方程式、内分、外分、直線の方程式、微分、積分など)を自動的に作成し、T_EX⁽⁶⁾ のソースファイルとして出力するとともに、その答えもT_EX のソースファイルとして出力するものである。
　現在、おおよそ問題作成の部分は完成し、ヘルプファイルの作成や内部処理の改善を行った後に、前記URLにアップロードする予定である。現在のところ、図7のようなユーザーインターフェイスであるが、まだまだ改良が必要かもしれない。



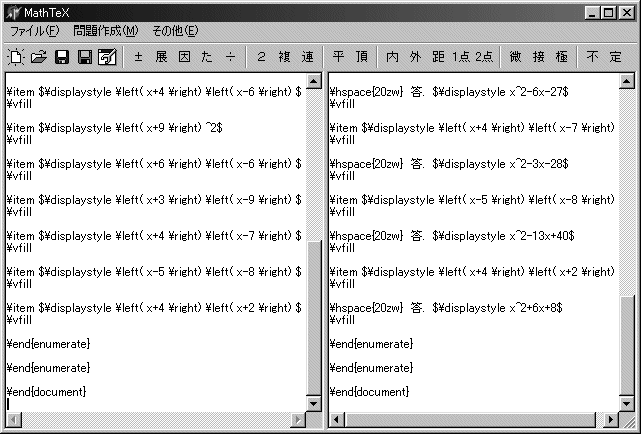
図7：MathT_EX を起動し、「展」ボタンを押すと




(6)フリーの組版ソフトで、数式のきれいな出力が特徴としてあげられる。アメリカのStanford大学のDonald E.Knuth教授が開発。その後、(株)アスキーが日本語化し、マクロを組み込んだpL^AT_E2e が広く普及している。ちなみに、この資料もT_EX で書かれている。

4.3　最後に

　今回の最大の問題点は、このソフトをいかに数学教育に結びつけるかである。実際には、完成して間もないため、1学期期末考査の解答作成のときに使用しただけで、授業などではまだ使用していない。授業や補習などで活用可能とも考えられるが、今後の課題としたい。
　次ページ資料にあるように、8月17日付のメール版「窓の杜」⁽⁷⁾(http://www.forest.impress.co.jp)の中で、MathCalcが紹介された。その中で、「夏休みの宿題の答え合わせや、中高生をもつお父さん・お母さんが子供の勉強を見てあげるときに使うといいだろう。」とあるように、学校教育の場のみならず、家庭教育の場でも活用されることを願うものである。
　最後になるが、これらのソフトをホームページ「数学のいずみ」からもダウンロード可能にしていただけると幸いである。また、これらのソフトに関する要望や疑問点、ソースファイルの希望があったら、KHC01517@nifty.ne.jpまでメールをいただきたい。

(7)(株)インプレス発行のメールニュースで、主にオンラインソフトの情報を扱っている。