嶥杫岤暿崅摍妛峑丂丂曅娸丂梞
丂悢妛嘥偺屄悢偺張棟傗妋棪偺暘栰偱丆埲慜偵弌戣偟偨拞偵師偺傛偆側栤戣偑偁偭偨丅偁傞惗搆偺夝摎偼丆庼嬈拞偵嫵偊偨撪梕丆偁傞偄偼婜懸偟偨傕偺偲偼堘偭偰偍傝丆偍傕偄傕傛傜側偄峫偊曽傪偟偨傕偺傕偁偭偨丅
| 丂俀寘偺帺慠悢偺偆偪偱丆廫偺埵偺悢偲堦偺埵偺悢偺榓偑婏悢偵側傞傕偺偼壗屄偁傞偐丅 |
佱嫵巘偺夝摎佲
佱惗搆偺夝摎佲
俋亊俆亖係俆乮屄乯
丂乮俀寘偺廫偺埵偺悢偼俋捠傝偁傞丅偦偺偦傟偧傟偵懳偟偰榓偑婏悢偵側傞偺偼俆捠傝偁傞偺偱丂俋亊俆亖係俆乮屄乯乯
俋侽亐俀亖係俆乮屄乯
丂乮俀寘偺惍悢偼慡晹偱俋侽屄偁傝丆婏悢偼偦偺敿暘偱丆俋侽亐俀亖係俆乮屄乯乯
| 丂嬫暿偺偮偐側偄敀嬍係屄丆愒嬍俀屄丆崟嬍俇屄偐傜俇屄傪庢傝弌偡曽朄偼壗捠傝偁傞偐丅偨偩偟丆庢傝弌偝側偄怓偺嬍偑偁偭偰傕傛偄丅 |
佱嫵巘偺夝摎佲
| 俛丗俇 | ||
| 俛丗俆丆倂丗侾 | 俛丗俆丆俼丗侾 | |
| 俛丗係丆倂丗俀 | 俛丗係丆倂丗侾丆俼丗侾 | 俛丗係丆俼丗俀 |
| 俛丗俁丆倂丗俁 | 俛丗俁丆倂丗俀丆俼丗侾 | 俛丗俁丆倂丗侾丆俼丗俀 |
| 俛丗俀丆倂丗係 | 俛丗俀丆倂丗俁丆俼丗侾 | 俛丗俀丆倂丗俀丆俼丗俀 |
| 俛丗侾丆倂丗係丆俼丗侾 | 俛丗侾丆倂丗俁丆俼丗俀 | |
| 俛丗侽丆倂丗係丆俼丗俀 |
佱惗搆偺夝摎佲
亂嶲峫亃
丂偦偺懠偺屄悢傊偺乕斒壔偼擄偟偄偲巚傢傟傞偑丆偨偲偊偽丆敀嬍係屄丆愒嬍俀屄丆崟嬍俆屄偐傜俇屄傪庢傝弌偡曽朄偼丆忋偺夝摎偐傜慡晹崟偺応崌傪彍偗偽椙偄偺偱丆
丂丂丂俆亊俁亅侾亖侾係乮捠傝乯
丂傑偨丆敀嬍係屄丆愒嬍俁屄丆崟嬍俇屄偐傜俇屄傪庢傝弌偡曽朄傕丆敀係屄丆愒俁屄偺応崌傪彍偗偽椙偄偺偱丆
丂丂丂俆亊係亅侾亖侾俋乮捠傝乯
偲摨偠傛偆偵媮傔傞偙偲偑偱偒丆偙偺峫偊曽傪梡偄偰媮傔傞偙偲偑偱偒傞丅
| 俙丆俛丆俠丆俢丆俤丆俥丆俧偺俉恖偑拪慖傪偟偰係恖丆俁恖丆侾恖偺晹壆偵偼偄傞偲偒丆俙丆俛偺俀恖偑摨偠晹壆偵擖傞妋棪傪媮傔傛丅 |
佱嫵巘偺夝摎佲
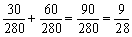
佱惗搆偺夝摎佲
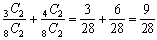
丂惗搆偺夝摎偵偼壗傕愢柧偑側偄偑丆幚嵺偵倫恖丆倯恖丆倰恖偱崌寁値恖傪晹壆偵擖傟傞応崌傪峫偊傞丅摿掕偺俀恖俙丆俛偑倫恖乮倫亞俀乯偺晹壆偵擖傞妋棪傪媮傔傞偲
丂丂丂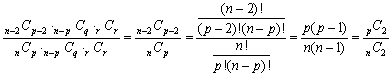
偲側傝丆偳傫側応崌偱傕惉傝棫偪偦偆偱偁傞丅
丂側偤偙偆側傞偐帺椡偱偼棟夝偱偒偢丆懠偺愭惗偵憡択偟偨偲偙傠丆堎側傞俉屄偺応強偵暲傋傞弴楍偱峫偊偰丆師偺夝摎傪摼偨丅
丂俉恖傪乕楍偵暲傋傞偺偼俉両乮捠傝乯丆俙丆俛偑俁恖晹壆偵擖傞偺偼俁亊俀乮捠傝乯丆偦偺懠偺暲傋曽偼俇両乮捠傝乯傛傝
丂丂丂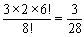
丂摨條偵俙丆俛偑係恖晹壆偵擖傞偺偼丆係亊俁乮捠傝乯丆偦偺懠偺暲傋曽偼俇両乮捠傝乯側偺偱
丂丂丂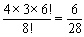
丂偮傑傝丆媮傔傞妋棪偼
丂丂丂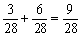
偲側傞丅
丂堦斒揑偵峫偊傞偲丆摿掕偺俀恖俙丆 俛偑倫恖乮倫亞俀乯偺晹壆偵擖傞妋棪偼丆堎側傞値屄偺弴楍偱峫偊偰丆
丂丂丂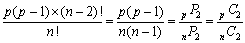
偲側傞丅
丂弴楍偲慻崌偣偺娭學偱偼丆崱擭偺帋尡偱傕帡偨傛偆側夝摎偑偁偭偨丅
| 丂晝曣俀恖偲巕嫙俁恖偺寁俆恖偑侾楍偵暲傇偲偒丆晝曣偑楍偺椉抂偵偔傞妋棪傪媮傔傛丅 |
佱嫵巘偺夝摎佲
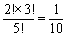
佱惗搆偺夝摎佲
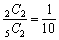
丂偙偺夝摎偼嬼慠偐傕偟傟側偄偑丆慜偺栤戣偲摨偠傛偆偵峫偊傞偙偲偑偱偒傞丅
丂俆恖傪乕楍偵暲傋傞偺偼俆両乮捠傝乯丆椉恊偑椉抂偵偔傞偺偼俀両乮捠傝乯丆偦偺懠偺暲傋曽偼俁両乮捠傝乯側偺偱
丂丂丂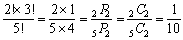
偲側傞丅
丂偙偺応崌偼俹偱傕俠偱傕摨偠摎偊偵側傞偑丆幚嵺偼俹偺寁嶼偱側偗傟偽丆峫偊曽偼惓偟偄偲偼尵偊側偄偐傕偟傟側偄丅晹暘揰傕娷傔偰摼揰偵偡傞偐偟側偄偐偼奺嫵巘偺敾抐偵傛傞偩傠偆偑丆巹偲偟偰偼丆乬媈傢偟偒偼儅儖乭偺偮傕傝偱惓夝偵偟偰偄傞丅
丂傔偭偨偵偼側偄偑丆帋尡偱惗搆偑柺敀偄敪憐傪偡傞偙偲偑偁傝丆恀寱偵庢傝慻傫偩摎埬偵偼丆巹偺曽偑峫偊偝偣傜傟丆擸傫偩夝摎傕偁偭偨丅傕偟偐偟偨傜崱傑偱傕偙傫側夝摎傪尒摝偟偰偄偨偐傕偟傟側偄丅傕偆彮偟拲堄偑昁梫偱偁傞偲幚姶偡傞偲嫟偵丆惗搆偺夝摎偐傜妛傇偙偲傕彮側偔偼側偄偙偲傪夵傔偰姶偠偰偄傞丅