丂娭悢偵偮偄偰偺奣擮偼丄帺慠傗幮夛偵偍偗傞尰徾偺拞偱丄偄偔偮偐偺娭楢偟偰曄壔偡傞検偺娫偺朄懃惈偵拝栚偡傞偙偲偐傜宍惉偝傟偰偒偨丅
 奣擮偺楌巎
奣擮偺楌巎
丂娭悢乮倖倳値們倲倝倧値乯偺岅傪梡偄巒傔偨偺偼俴倕倝倐値倝倲倸偱偁傞丅斵偼偙偺岅傪柧妋偵掕媊偼偟側偐偭偨偑丄侽傗侾偺傛偆側掕悢偵懳偟丄曄摦偡傞検乮曄検傑偨偼曄悢乯倶傪峫偊丄曄悢倶偲偲傕偵曄摦偡傞曄悢乮椺丂x2丄倢倧倗倶丄倱倝値 倶丂側偳乯傪x偺敓悢偲屇傃丄x偺娭悢傪堦斒揑偵昞偡婰崋偲偟偰丂倖乮倶乯丆冇乮倶乯側偳傪梡偄偨丅
丂俤倳倢倕倰偼敓悢傪掕媊偟偰乬曄悢偲掕悢偐傜慻傒棫偰傜傟偨夝愅揑側幃乭偲偄偭偰偄傞丅乮侾俈係俉擭乯
丂俠倎倳們倛倷偼乬懡偔偺曄悢偺娫偵埥傞娭學偑偁傝丄偦偺偆偪偺侾偮偺抣偲偲傕偵懠偺傕偺偺抣偑掕傑傞偲偒偼丄捠忢偦偺侾偮偺曄悢偵傛偭偰懠偺傕偺傪昞偟偰峫偊傞丅偦偺偲偒丄偙偺侾偮偺傕偺傪撈棫曄悢偲屇傃丄懠偺傕偺偼偦偺敓悢偱偁傞偲偄偆丅乭偲弎傋偰偄傞丅乮侾俉俀俁擭乯
丂Dirichlet偼乬y偑慡嬫娫偵偍偄偰摨堦偺朄懃偵廬偭偰x偵娭學偡傞偙偲傪梫偟側偄偺傒側傜偢丄偦偺娭學偑悢妛揑嶼朄偵昞偝傟傞昁梫傕側偄乭偲偄偄丄敓悢偼寢嬊懳墳偵懠側傜側偄偙偲傪柧傜偐偵偟偨丅崱擔丄敓悢偼懳墳偺暿柤偲峫偊傜傟偰偄傞丅乮埲忋丄娾攇悢妛帿揟乯
 娭悢偺悢妛揑側掕媊
娭悢偺悢妛揑側掕媊
丂俀偮偺廤崌M,N偑偁偭偰丄M偺擟堄偺尦x偵懳偟偰N偺侾偮偺尦倷偑妋掕偡傞偲偒丄偙偺x偐傜y傊偺懳墳偺婯懃f傪M偐傜N傊偺幨憸偁傞偄偼娭悢偲偄偭偰丄
丂丂丂倖丟丂x伕俵丂仺丂倷亖倖乮倶乯伕俶
偁傞偄偼
丂丂丂倖丟丂俵丂仺丂俶
偲昞偡丅
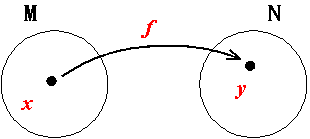 丂偙偺偲偒丄俵傪娭悢倖偺掕媊堟丄俶傪倖偺抣堟偲偄偆丅傑偨丄倶傪撈棫曄悢丄倷傪廬懏曄悢偲偄偆丅倶丄倷偼悢偱側偔偰傕丄悢偺慻丄儀僋僩儖丄偦偺懠壗傜偐偺廤崌偺尦偱偁傟偽傛偄丅
丂偙偺偲偒丄俵傪娭悢倖偺掕媊堟丄俶傪倖偺抣堟偲偄偆丅傑偨丄倶傪撈棫曄悢丄倷傪廬懏曄悢偲偄偆丅倶丄倷偼悢偱側偔偰傕丄悢偺慻丄儀僋僩儖丄偦偺懠壗傜偐偺廤崌偺尦偱偁傟偽傛偄丅
丂丂娭悢偵偼
丂丂丂丂嘆丂楢懕揑曄悢偵傛傞娭悢
丂丂丂丂嘇丂棧嶶揑曄悢偵傛傞娭悢
偑偁傞偑丄廤崌偐傜廤崌傊偺幨憸偲偄偆揰偱偼摨偠偱偁傞丅娭悢偲偼偒傢傔偰峀偄撪梕傪傕偭偨奣擮偱偁傝丄懳墳丄幨憸丄曄姺丄憖嶌偲偄偆柤偱抲偒姺偊傜傟傞朙晉側撪梕傪傕偭偰偄傞丅嵟弶偵乬娭悢偲偼壗偐乭傪弎傋傞偲偒偵丄娭悢偺偝傑偞傑側堄枴偺奼挘偵揔墳偱偒傞傛偆側宍偱傑偲傔偰偍偐側偗傟偽側傜側偄丅娭悢倖偺傕偮摥偒傗丄懳墳偺偝偣曽偑梕堈偵巚偄晜偐傋傜傟傞傛偆側僔僃乕儅傪岺晇偡傞偙偲偑昁梫偱偁傞丅
丂偙偺傛偆側僔僃乕儅偲偟偰揔摉偲峫偊傜傟傞偺偑僽儔僢僋丒儃僢僋僗乮埫敔乯偱偁傞丅僽儔僢僋丒儃僢僋僗偼丄撪晹偺偐傜偔傝偑偳偆側偭偰偄傞偐偼暿栤戣偲偟偰丄偲偵偐偔壗傜偐偺巇妡偗偵傛偭偰堦掕偺憖嶌傪峴偆憰抲偱偁傞丅擖偭偰偔傞傕偺乮擖椡乯偵壛岺傪巤偟偨傕偺乮弌椡乯傪奜晹偵憲傝弌偡摥偒傪傕偭偰偄傞丅僽儔僢僋丒儃僢僋僗偼僲僀儅儞偑岲傫偱梡偄偨僔僃乕儅偱丄斵偼僆乕僩儅儞偺棟榑揥奐偱偟偽偟偽偙傟傪棙梡偟偰偄傞丅
 僽儔僢僋丒儃僢僋僗偲娭悢
僽儔僢僋丒儃僢僋僗偲娭悢
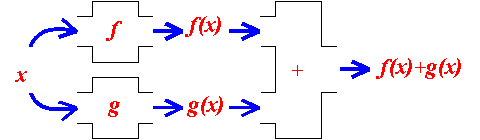
 丂塃偺恾偺堄枴偼擖椡倶偑倖偺憖嶌傪宱偰弌椡偑倷偲側偭偰弌偰偒偨偲偄偆偙偲偱偁傞丅偙傟傪幃偱偼丂倷亖倖乮倶乯丂偲彂偗傞丅倖乮倶乯偺乮丂乯偼擖椡偺擖傝岥偲峫偊傞偙偲偑偱偒傞丅
丂塃偺恾偺堄枴偼擖椡倶偑倖偺憖嶌傪宱偰弌椡偑倷偲側偭偰弌偰偒偨偲偄偆偙偲偱偁傞丅偙傟傪幃偱偼丂倷亖倖乮倶乯丂偲彂偗傞丅倖乮倶乯偺乮丂乯偼擖椡偺擖傝岥偲峫偊傞偙偲偑偱偒傞丅
丂娭悢偺榓偺椺偲偟偰
丂丂倖乮倶乯亖俁倶俀丆倗乮倶乯亖係俉倶丂偺偲偒 倖乮倶乯亄倗乮倶乯亖俁倶俀亄係俉倶丂摍偲側傞丅
丂媡娭悢倖亅侾偼丄傕偲偺娭悢倖偲媡偺憖嶌傪峴偆娭悢偱偁傞偐傜丄偙傟偼僽儔僢僋丒儃僢僋僗偺擖椡偲弌椡傪媡揮偟偰峫偊傟偽傛偄丅晛捠偺憰抲偱偼堦斒偵壜媡偱側偄偑丄巚峫偺忋偱偼媡揮偟偰峫偊傞偙偲偑偱偒傞丅

丂崌惉娭悢偼俀偮偺僽儔僢僋丒儃僢僋僗傪捈楍偵偮側偖偲傛偄丅倖偺弌椡偑倗偺擖椡偵側偭偰偄傞応崌偵偼丄俀偮偺僽儔僢僋丒儃僢僋僗倖丄倗傪侾偮偺傑偲傑偭偨僽儔僢僋丒儃僢僋僗偲傒傟偽偙偺怴偟偄僽儔僢僋丒儃僢僋僗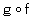 偑倖偲倗偺崌惉偲側傞丅
偑倖偲倗偺崌惉偲側傞丅
 丂
丂
 丂
丂