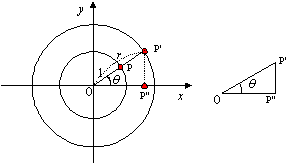
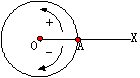
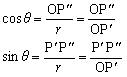 丂偙偺偙偲偐傜惓丆晧偺妏搙偑懚嵼偡傞偙偲丆傑偨360亱埲忋偺妏搙傕懚嵼偡傞偙偲偑帺慠偵摫偐傟傞丅偙偺傛偆側墌廃忋偺揰偺塣摦偺拞偱嵟傕婎杮揑側傕偺偼扨埵墌廃忋偺揰偺塣摦偱偁傠偆丅嵗昗暯柺偱扨埵墌傪峫偊丆揰A偺嵗昗傪(1丆0)偲偡傞丅尨揰傪O丆偙偺扨埵墌廃忋偺揰傪P偲偡傞偲偒丆P偺嵗昗(x丆y)偼佢AOP偵傛偭偰寛掕偝傟傞丅偟偨偑偭偰佢AOP=兤傪帺慠悢偲偟丆x丆y傪廬曄悢偲偡傞娭悢偑偦傟偧傟峫偊傜傟傞丅
丂偙偺偙偲偐傜惓丆晧偺妏搙偑懚嵼偡傞偙偲丆傑偨360亱埲忋偺妏搙傕懚嵼偡傞偙偲偑帺慠偵摫偐傟傞丅偙偺傛偆側墌廃忋偺揰偺塣摦偺拞偱嵟傕婎杮揑側傕偺偼扨埵墌廃忋偺揰偺塣摦偱偁傠偆丅嵗昗暯柺偱扨埵墌傪峫偊丆揰A偺嵗昗傪(1丆0)偲偡傞丅尨揰傪O丆偙偺扨埵墌廃忋偺揰傪P偲偡傞偲偒丆P偺嵗昗(x丆y)偼佢AOP偵傛偭偰寛掕偝傟傞丅偟偨偑偭偰佢AOP=兤傪帺慠悢偲偟丆x丆y傪廬曄悢偲偡傞娭悢偑偦傟偧傟峫偊傜傟傞丅
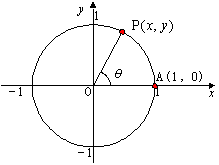 丂傑偨丆摦宎OP偺孹偒傕兤傪帺慠悢偲偡傞偲偒偺廬曄悢偱偁傞偲峫偊傜傟傞丅偦偙偱師偺嘆丆嘇丆嘊偺傛偆偵掕媊偡傞丅
丂傑偨丆摦宎OP偺孹偒傕兤傪帺慠悢偲偡傞偲偒偺廬曄悢偱偁傞偲峫偊傜傟傞丅偦偙偱師偺嘆丆嘇丆嘊偺傛偆偵掕媊偡傞丅
丂扨埵墌廃忋偺揰P偺嵗昗傪(x丆y)丆摦宎OP偺妏搙傪佢AOP=兤偲偟偰昞偡偲偒
丂丂丂x=cos兤 乧嘆丆y=sin兤 乧嘇丆丂丒丒丒
丂丂丂(摦宎偺孹偒乯=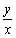 =tan兤 乧嘊
=tan兤 乧嘊
丂偟偨偑偭偰丆tan兤=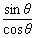 乧嘋偲偡傞丅
乧嘋偲偡傞丅
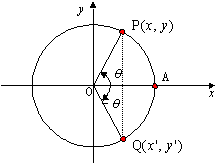 丂師偵揰P偺x幉偵娭偡傞懳徧揰傪Q偲偟嵗昗傪(x'丆y')偲偡傞丅偙偺偲偒摦宎OP偺妏搙偼兤偱丆摦宎OQ偺妏搙偼-兤偱偁傞偐傜丆嘆丆嘇偺掕媊傛傝
丂師偵揰P偺x幉偵娭偡傞懳徧揰傪Q偲偟嵗昗傪(x'丆y')偲偡傞丅偙偺偲偒摦宎OP偺妏搙偼兤偱丆摦宎OQ偺妏搙偼-兤偱偁傞偐傜丆嘆丆嘇偺掕媊傛傝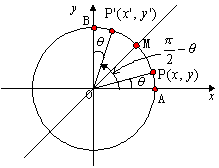 丂師偵扨埵墌廃忋偺揰P丆P'偵偮偄偰摦宎OP偺妏搙偑兤丆OP'偺妏搙偑
丂師偵扨埵墌廃忋偺揰P丆P'偵偮偄偰摦宎OP偺妏搙偑兤丆OP'偺妏搙偑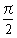 -兤側傜偽P偲P'偼捈慄y=x偵娭偟偰懳徧偱偁傞丅揰(0丆1)傪B偲偡傞偲佢BOP'=兤丅摦宎OM偺妏搙傪
-兤側傜偽P偲P'偼捈慄y=x偵娭偟偰懳徧偱偁傞丅揰(0丆1)傪B偲偡傞偲佢BOP'=兤丅摦宎OM偺妏搙傪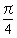 偲偡傞偲
偲偡傞偲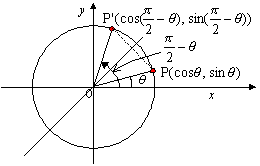
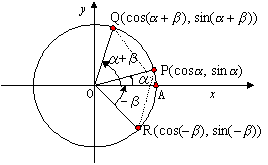
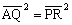 傛傝
傛傝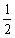 {sin(兛+兝)+sin(兛-兝)} 乧嘙
{sin(兛+兝)+sin(兛-兝)} 乧嘙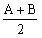 丆兝=
丆兝=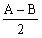 偲側傝
偲側傝