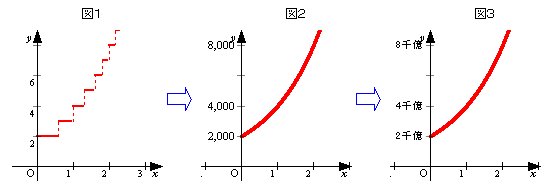
指数現象のモデルとしてバクテリアの例がよく利用されている。10時間毎に2倍ずつ増えてゆくバクテリアについて調べてみよう。
はじめに着目したのが2個のバクテリアがどのように変化してゆくかについて考える。2個のバクテリアが同時に分裂するのではないという状況から出発してみよう。2個のものがある時間を経過したあとに3個となり,4個,5個,・・・,8個・・・となってゆくが,ある時刻から,ある時刻との間においてはバクテリアの分裂は起きていないので,その間のバクテリアの個数は変化しないということになる。このバクテリアを1万個とか10万個とかの単位で大量に観察してみるとどうなるであろうか。
ある時刻に分裂するバクテリアと次に分裂するバクテリアの間の時間間隔は非常に小さなものとなり,バクテリアの個数が多ければ多いほど分裂と分裂の時間間隔は微小なものとなってゆき,ついには無視してよいことになってゆくであろう。つまり観察しているバクテリアの量が多ければ多いほど,その変化の仕方はなだらかで次第に連続的な曲線とみなしてよいことになってゆく。
以上述べてきた状況を示しているのが,図1,図2,図3のグラフである。

そこで大量のバクテリアを観察する例をとりあげるには,10時間毎に重さが2倍ずつ増えてゆくというように,個数が増加してゆくイメージから,重さが倍変化してゆくというイメージを切り替えて考えているのである。つまり本来は個数の増殖という離散的変化としての現象を重さの倍変化という連続的変化として捉えなおしているのである。
放射能の現象なども,指数関数で表すことができる。個々の原子の出す放射能は離散的な値なのであるが,何百グラムかの放射能物質の中には6×1023個等という膨大な量の原子が含まれている。このことから放射能の減少はなだらかに連続的に変化してゆくと考えてよいのである。
2つの例について考察したが,本来は離散的な変化である現象も,大量現象の観察という場合には連続的変化とみなすことが可能である。
指数関数のモデルとして,バクテリアの増殖とか,放射能の現象などをとりあげるとき,これを前提として考えていることに注意する必要がある。
実験法則によるとある媒質を通る光で、光の方向に垂直な平面を通る光の量は単位距離進むごとに1/a倍となってゆく。
(図1)はそのような状況を略図で示したものである。
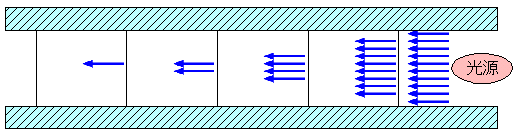
(図2)のように直方体でできている媒質があり、光がこの中を通り抜けてゆくとする。この図には書いてないが、この媒質の周囲は一切光を通さない物質でおおわれていて光源を発した光はこの直方体の中だけを通ってゆくことができるようになっている。
また発せられる光の量は常に一定で図の右から左の方向へと直進しているものとしよう。この直進している光の方向に沿って、数直線が図の如く設定されている。
またこの数直線に垂直な平面による直方体の切り口が、
AxBxCxDx、A1B1C1D1、A0B0C0D0、A-1B-1C-1D-1、…
等であるとする。
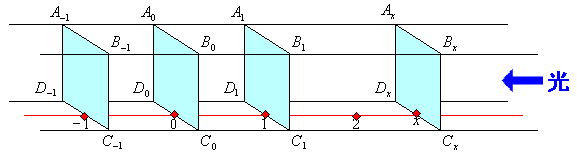
光は直方体の内部を通りながら、この媒質に少しずつ吸収されてA0B0C0D0面を通る光の量はA1B1C1D1面を通る光の量の1/a倍になっている。またA-1B-1C-1D-1面を適る光の量はA0B0C0D0面を通る光の量の更に1/a倍になっている。このことはA0B0C0D0面を違る光の量を基準にして考えると、観測者がA0B0C0D0面から光源に向って単位距離だけ進むと光の量はa倍になって観測され、光源から遠去かるように単位距離だけ進むと光の量は1/a倍になったとして観測されるということである。またこの媒質はどの位置においても物質の構成は一様であれば、どの位置を基準にしても光源に向って単位距離だけ進むとそこでの光の量は出発点での光の量のa倍になっていることにも注目しておくこととしたい。しかもA0B0C0D0面を通る光の量はA1B1C1D1面を通る光が単位距離だけ光源より遠去かって急に1/a倍の量になったということではない。
A1B1C1D1面から少しでもA0B0C0D0面に向って進むとき、光は進むにつれて吸収され続けて単位距離だけ進んだ時点で1/a倍となっているということである。
逆に観測者がA0B0C0D0面からA1B1C1D1面に向って進んでゆく場合、それぞれの点での面を通る光の量は次第に増加しつつ単位距離だけ進んだA1B1C1D1面に於いてはa倍になっているということになるのである。
今後簡単に表現する為に、面A0B0C0D0を通っている光とか、面AxBxCxDxを通っている光という代りに、目盛0を通っている光,目盛xを通っている光という表現を用いることにしたい。
更に筒略化して、目盛0における光とか目盛xにおける光等という表現を用いたとしても、(図2)の状況を想起するならぱ内容に混乱を起こすことはないと思われる。
今、目盛りがxの位置を通る光の量をIxと表わすとき次のことがいえる。
I1=aI0、I2=aI1=a2I0、I3=aI2=a3I0、…
そしてxが整数でない場合でも
I5/2=a5/2I0
等と表わすことかできる。
またxは負数であってもかまわない。目盛0の位置から左に1m離れた位置は−1の位置、左に2m離れた位置は目盛−2の位置と呼べばよく、既に考察してきたように
I-1=a-1I0、I-2=a-2I0、…、I-y=a-yI0 (y>0)
と表わすことができる。
特に0の位置では0の位置より零m進んだ位置と考えれぱよいから、そこを通る光の量については、I0=a0I0が成り立つ。
従ってa0=1となる。
このようにして、xがあらゆる実数の値をとるとき、Ix=axI0の関係が成り立つ。では以上のようにして定義されたaxという数はどのような性質を持つ数なのであろうか。
次に、x>0として、-xの位置を通る光の量は0の位置を通る光の量の何倍なのかに着目してみよう。まずI-x=a-xI0である。
また観測者が−xの位置から光源に向ってxm進むと0の位量に達するのであるから、I-x×ax=I0となる。
故にI-x=I0/ax。従って a-x=1/ax が導かれる。
I-1はI0の1/a倍、I-2はI-1の1/a倍、……
となっているので、つまり0から負の方向に1m進むごとに光の量は1/a倍になってゆく。
1m進むごとに光の量はa倍になってゆくとき、xm進むならぱax倍となるので、この考えを進めてゆくと、1m進むごとに1/a倍となる光の量は、xm進むならば (1/a)x 倍になるということになる。
よって I-x=(1/a)xI0 となる。以上より
(1/a)x=a-x=1/ax
が成り立つ。
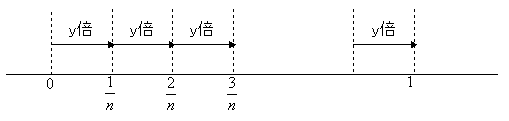
I1/n=a1/nI0 のときはy=a1/n とおいて、このyについて考えてみよう。
ただし、nは自然数である。これは1/n進むごとにy倍となることをくり返しているから次の関係が成り立つ。
I1/n=yI0、I2/n=yI1/n=y2I0、…
より
I1=yI(n-1)/n=ynI0
となる。ところで、I1=aI0 より yn=a、y=n√a
従って
a1/n=n√a
が成り立つ。
次にmも自然数として、mの位置での光の量はIm=amI0 となっている。これをn段階に分割して考えてみよう。
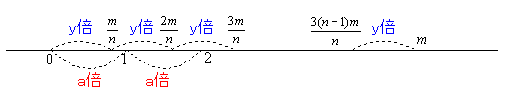
Im/n=am/nI0であるがy=am/nとおいて、このyについて考えよう。
m/nだけ進むごとにy倍になることをn回くり返してmの位置に達している。従って
Im/n=yI0、I2m/n=yIm/n=y2I0、……、Im=yI(n-1)m/n=ynI0
またIm=amI0であるからyn=amとなる。
故にy=n√am が成り立つ。
以上xが有理数の場合のaxの意味について述べてきた。ではxが無理数の場合はどのような意味を持つのだろうか。
3√2と5πを例として考察してみよう。
√2=1.4142135・・・・であるから
1.414<√2<1.415、1.4142<√2<1.143・・・
となり√2はこれにいくらでも近い有理数で範囲を限定することができる。従って
31.4<3√2<31.5、31.41<3√2<31.42、31.414く3√2<31.415・・・
と3√2はどんどんある値に近づく。この値を3√2と呼ぶのである。
また次のような考え方でもよい。π=3.14159265・・・であるから
3.1、3.14、3.141、3.1415、3.14159・・・
という列は次第にπに近づいてゆく。そこで
53.1、53.14、53.141、53.1415、53.14159・・・
という列が次第に近づいてゆく数を5πと呼ぶのである。
このようにして、axはxが有理数である場合をもとにしてxが無理数の場合にも説明できるので、xが実数の場合のaxの意味が明らかになったといってよいのである。
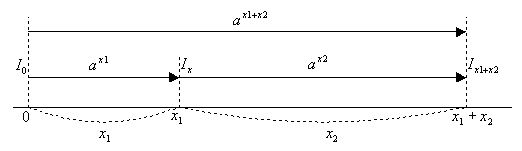
各点を通過している光の量に着目すると、
Ix1=ax1I0、Ix1+x2=ax2Ix1
より
Ix1+x2=ax2(ax1I0)=ax1×ax20
となる。また
Ix1+x2=ax1+x2I0
なので
ax1×ax2=ax1+x2
が得られる。
次にIx1=bI0とする。このときIx1=ax1I0であるからb=ax1である。0から目盛りx1までの距離を新しく単位距離と見なしたとき、0から目盛りx1x2までの距離はこの新単位距離のx2倍となっている。
さて観測者が0を出発して光源に向って距離x1x2だけ進んだ状況について考えてみよう。
これは観測者が新単位距離を進むごとに光の量はb倍になりつつ、その新単位距離のx2倍の距離を進んでいるのである。
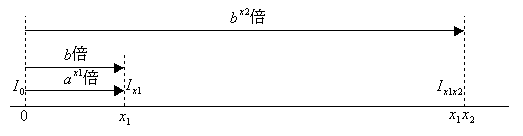
目盛りx1x2を通る光の量はIx1x2=bx2I0である。またIx1x2=ax1x2I0であるからbx2=ax1x2となる。b=ax1より
(ax1)x2=ax1x2
となる。
次に0から光に向って1m進むと、光の量がab倍となる媒質中を通る光については、
I1=abI0
が成り立つ。
このI1については、次のように段階に分けて考えることができる。まず0から光に向って1m進むごとに光の量がa倍となる媒質の中を1m進む。このときの光の量をI'1とするとI'1=aI0である。ひき続いて光に向って1m進むごとに光の量がb倍になる媒質の中を1m進む。このときの面を通る光の量をI''1とするとI''1=bI'1となる。
よって
I''1=bI'1=b(aI0)=abI0
となりI''1=I1がいえる。
つまり光の量に着目する時、1m進むごとにab倍となる媒質の中を1m進むということは、1m進むごとにa倍となる媒質の中を1m進み、引き続いて1m進むごとにb倍となる媒質の中を1m進むということと同じことになるのである。この考えをつきつめてゆくと、0から光に向って1m進むごとにab倍となる媒質の中をxm進んだときの光の量は、0からまず光に向って1m進むごとにa倍となる媒質の中をxm進み、ひき続いて光に向って1m進むとb倍となる媒質の中をxm進んだときの光の量と同じになるのである。
まず1m進むごとにab倍となる媒質中をxm進むとIx=(ab)xI0となる。
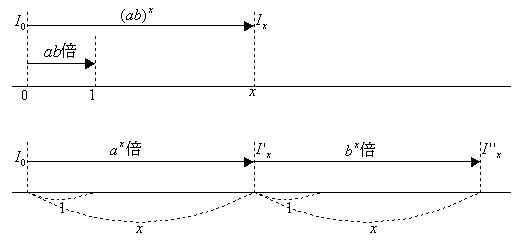
0からある媒質中を光に向ってxm進んだときの光の量は1m進むごとにa倍になるとするとI'x=axI0で得られる。続いてすぐ1m進むごとにb倍となる媒質中をxm進んで光の量はI''xとなったとすれば、I''x=bxI'xとなる。
従って
I''x=bxI'x=bx(axI0)=axbxI0
となる。既に考察してきたようにIx=I''xであるから
(ab)x=axbx
が成り立つ。
以上のことから指数法則といわれる計算公式は実数の範囲で成り立つといってよいのである。
指数関数y=axにおいては、xのあらゆる実数値に対応してaxの値が存在するということについての理解が大切であるが、これは光のモデルを思い起こすことによってすぐに納得できることであろう。
またx1x2がどれ程接近した実数値であっても、a>1の場合にx1<x2ならぱax1<ax2である。
これは指数関数の連続性に対する理解に大いに役立つものである。
また(図2)のようなモデルは、少し視点を変えれば対数関数の性質を導いてゆくことにも活用されるのである。
例として、0から光に向って1m進むごとにa倍となる媒質中を進む光に対して、0からどれだけ進むと光の量は2倍となるのかについて考えよう。
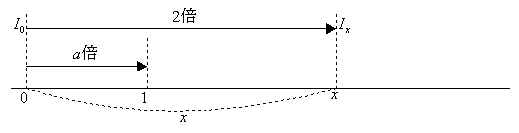
これはIx=2I0でIx=axI0であるから、ax=2となるxを求めることになる。ここからloga2=xを定義するのは自然の成り行きであろう。
対数の諸性質も光のモデルを念頭におきながら導いてゆくことができる。
また指数関数、対数開数の微積分についても〈図2)のモデルを使って考察することができる。これらのことについては別な機会で述べてみたいと思う。