教　具　の　工　夫

〜いくつかの実例〜

はじめに

　理科の場合は年間の始めから終わりまで全く実験なしの授業などというものは考えられないであろう。これに比べて、数学の場合はチョークと黒板という伝統的な授業スタイルに対してはあまり疑問を持たれることもない。最近は先進的な試みに積極的な何人かの教師たちが、コンピュータを活用しつつ授業を展開してゆく工夫もされてきてはいる。
　授業内容の活用化のためには、コンピュータや教具、模型や、時には紙芝居のようなものなどを利用することも必要である。
　またゲームや実験、ストーリーなどを組織してゆくことも大切な工夫のひとつであろう。
　そして、これらを含めた豊かな授業の中で学習者の中に、数学的構造が理解されてゆくのであると思われる。

空間の目盛り -空間座標モデル-

　空間座標や空間ベクトルを説明する際にまずぶつかる困難な点がある。
　その最大の原因は2次元の黒板の上に3次元のものを書き表そうとするところにある。学習者は2次元の平面上に書き表された空間座標や、空間ベクトルの図を見ても、その図を通して空間への認識を深めてゆくことが決して容易ではないのである。
　図のような空間座標を示す図も、現実に空間座標のモデルを観察した後ではイメージの定着も早いのである。
　私は最近空間座標のモデルを出来るだけ活用して授業を展開することにしている。またこのモデルを使って、空間ベクトルの次のような諸公式も説明してしまうことにしている。
(a₁,a₂,a₃)+(b₁,b₂,b₃)=(a₁+b₁,a₂+b₂,a₃+b3)
(a₁,a₂,a₃)-(b₁,b₂,b₃)=(a₁-b₁,a₂-b₂,a₃-b3)
k(a₁,a₂,a₃)=(ka₁,ka₂,ka₃)
2点 A(a₁,a₂,a₃)，B(b₁,b₂,b₃) について
　　　
　　　
　

変動する最大値、最小値　-紙芝居式 M,m 説明器-

　2次関数の最大値、最小値の問題で入試等でよく出題され、昔から難問といわれ、教師も説明するのに苦慮するという問題がある。その代表的なのは次の［1］,［2］,［3］のような問題であろう。

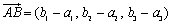
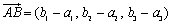
［1］2次関数 y=x2-4x+5 のの区間 a≦x≦a+2 における最大値を M(a)、最小値を m(a) とするとき、M(a)、m(a)をaの式で表わせ。

［2］区間 0≦x≦2 における関数 y=2x2-4ax+1 の最大値と最小値、及びそのときの x の値を求めよ。

［3］区間の 0≦x≦a における y=x2-4x+3 の最大値・最小値とそのときの x の値を求めよ。

　これらの問題に共通していることは文字 a に関して場合分けが必要であり、説明する際には多くのグラフを書いたりすることになるが、場合分けが動きとしてとらえ難くなかなか理解しづらいということである。この難点を少しでも軽減させたいと、いくつかの教具を製作してみたが、私はこれを“紙芝居方式M,m説明器”と呼んでいる。今回はこれらの教具の実演も拭みてみたいと思う。

　
　

軌跡の方程式<動点が複数個の場合)　-ジェラシー大作戦-

　動転が複数個の場合の軌跡の方程式は、なかなか説明するのに苦労がつきまとう。ゴムひもを利用した教具を利用するのもひとつの方法であろう。
　私は、軌跡をえがくそれぞれの点に性格をつけ、ある種のストーリーをもとにして点と点の関連を考えさせることにしている。ジェラシー大作戦と名づけて説明しているのだが、次のようなものである。

　ある高校にアイドルちゃんと呼ばれる女の子がいる。彼女は容姿もプロポーションも抜群で、しかも努力家であると言う。彼女は陸上部に所属し、放課後はいつも陸上グランドで走る練習をしている。　一方、あこがれ君は同じ学校でのサッカー部のゴールキーパーである。アイドルちやんに熱烈に恋焦がれており、放課後はゴールキーパーの位置から走っている彼女に、いつもラブサインを送り続けている。
　このことを知ったジェラシー君の心境はおだやかではない。彼は、あこがれ君の意図をなんとか妨害しなければと固く決意し、視察を続けた結果、次のことに気がついた。
　アイドルちゃんと、あこがれ君を結ぶ線分を2:1 に内分する点に彼が立つと、彼にさえぎられてあこがれ君からはアイドルちやんが見えなくなってしまうのである。
　ジェラシー君の妨害作戦が成功するためには、彼はどのような走り方(動き)をしたらよいだろうか。

　注:このような問題を「ジェラシー大作戦」と呼んで数学教育の上では有名な問題である。

　アイドルちやんは、中心が原点、半径3の円周上を動くものとし、あこがれ君は定点(6,0)として、ジェラシー君の描く軌跡の方程式を求めよ。


今後に向けて

　関数の概念について説明しようとしていろいろ苦労したことがある。以前の教科書には対応図を使って関数とは「対応の規則」であることを説明しようとした。しかし、これは完全に失敗だったと思う。「対応」を理解させるのに対応図が決して適していた訳ではなかったようだ。
　いろいろ悩んだ後で、手作りのブラックボックスで説明を試みた。生徒たちの反応がもるで違うのである。授業に関心や興味を持つというよりも、むしろ感動しているといってよい程の表情なのであった。
　それ以来、私は関数の指導に、手作り教具としてのブラックボックスは欠かせないものと考えるようになった。
　授業の中での他の教材でも、教具が役立つ分野がまだまだあるように思われる。
　今回は、最近の授業で試みた例について発表することにしたが、今後作りたいと思っているいくつかの教具もある。
　それらについては別な機会に発表したいと思っている。