検亅幨憸亅悢
乣丂拪徾悢妛偲偼堦枴堘偆悢偺棟榑乮彉偺晹乯乣
憃梩崅摍妛峑丂戝嶳丂惸亂侾亃偼偠傔偵
丂悢偲偼壗偐丅埥偼悢偺棟榑偲偼偳偺傛偆偵偟偰憂傝忋偘傜傟偨偺偐丠丂偙偺傛偆側栤偵偼婛偵侾俋悽婭拞偵彁柤側悢妛幰払偵傛偭偰徻嵶偵尋媶偝傟棟榑壔偑姰惉偝傟偰偄傞偲偄偭偰傛偄偺偱偁傠偆丅椺偊偽僨僨僉儞僩偺挊嶌偲偐丄儔儞僟僂偺夝愅妛偵娭偡傞愱栧彂偺拞偱偙偺傛偆側棟榑揥奐傪尒傞偙偲偑偱偒傞丅傑偨擔杮偵偍偄偰傕崅栘掑帯挊"悢偺奣擮"偱悢偺棟榑偲偼偳偺傛偆側傕偺側偺偐偵偮偄偰柧妋偵弎傋傜傟偰偄傞丅丂偙傟傜偵偮偄偰峫偊傞偲偒"悢偺棟榑"偲偼姰惉偝傟偨棟榑偱偁傝丄怴偟偄堄枴偱偺"悢偺棟榑"側偳偼昁梫偱傕側偄偟丄傑偨怴偟偄棟榑傪憂傝忋偘傞梋抧傕側偄偐偺傛偆偵尒偊偰偔傞丅
丂偲偙傠偱丄俀侽悽婭拞崰偐傜僽儖僶僉偲柤偺傞悢妛幰偺僌儖乕僾偑惛椡揑偵悢妛偺彅暘栰偵傢偨偭偰偺挊嶌傪敪昞偟懕偗傞傛偆偵側偭偨丅斵摍偺朿戝側挊嶌廤"悢妛尨榑"偺拞偵偼丄廤崌丄幨憸偐傜巒傑偭偰悢偺棟榑偑揥奐偝傟偰偄傞丅偦偺拞偱帺慠悢榑偺晹暘偩偗偱傕丄僽儖僶僉偲崅栘掑帯偺挊嶌偵偼戝偒側堘偄偑偁傞丅愱栧壠偺夝愢傪撉傓偲僽儖僶僉偺帺慠悢榑偼婎悢榑揑帺慠悢榑偲傛偽傟丄崅栘掑帯挊偱偺帺慠悢榑偼彉悢榑揑帺慠悢榑偲傛偽傟傞傕偺偱擇偮偺帺慠悢榑傪戙昞偡傞傕偺偱偁傞偲偄偆丅偙偺傛偆偵悢偺棟榑偺拞偱傕丄偦傟偧傟偺堘偄偲摿挜傪帩偭偨棟榑偑偁傞偲尵偭偰傛偄偺偩偑丄偙傟傜偺挻桳柤側棟榑偼偄偢傟傕旕忢偵拪徾揑偱偁傝丄偐偮尰幚偺検偲偺娭楢偼幪徾偝傟偨拞偱憂傝忋偘傜傟偰偄傞丅
丂侾俋俈侽擭戙偵擖偭偰偐傜検偲悢偲偺娭楢傪廳帇偟丄検偺岞棟傪慜採偲偟偰検嬻娫偵偍偗傞曄姺偲偟偰悢偺棟榑傪憂傝忋偘傞乗乗偙偺傛偆側棟榑偑敪昞偝傟偨丅
丂撿塤摴晇攷巑偵傛偭偰採彞偝傟偨棟榑偲丄揷懞擇榊巵偵傛傞検偲悢偺棟榑偲偱偁傞丅偙傟傜偺棟榑偼暔棟妛傗壔妛偦偺懠偺彅壢妛偱柧傜偐偵偝傟偨偝傑偞傑側検偵偮偄偰偺惈幙傪傆傑偊偰悢偺棟榑傪憂傝忋偘偰備偙偆偲偄偆堦抳偟偨峫偊偺傕偲偵揥奐偝傟偰偄傞丅
亂俀亃廤崌丄幨憸丄検
丂偳偺傛偆側棟榑偱傕偦偺棟榑傪悇偟弝傔偰備偔応崌偺慜採傪柧妋偵偟偰偍偔昁梫偑偁傞丅丂揷懞棟榑偱偼傑偢廤崌偲幨憸偵偮偄偰婎杮揑側奣擮傪妋擣偡傞偙偲偐傜巒傔傜傟偰偄傞丅廤崌偵偮偄偰偺曪娷娭學偲偐丄梫慺偲廤崌偺娭學丄晹暘廤崌丄曗廤崌丄摍偟偄廤崌摍偺婎杮揑惈幙偼婛抦偺傕偺偲偟偰峫偊偰偄傞丅師偵幨憸丄摍偟偄幨憸丄幨憸偺榓丄幨憸偺崌惉丄幨憸偺崌惉偵偍偄偰偼寢崌懃偼惉傝棫偮偑丄岎姺懃偼偼惉傝棫偨側偄丄媡幨憸偼偳偺傛偆側応崌偵懚嵼偡傞偐丄幨憸偵偍偄偰尨憸偲憸偺懚嵼偡傞廤崌偑摨偠応崌偵幨憸傪曄姺偲屇傇偙偲丄摍傪妋擣偟偰偍偒偨偄丅
丂偙傟傜偼偡傋偰"悢"偲偼娭學偺側偄奣擮側偺偱丄偁傜偐偠傔廤崌傗幨憸偵偮偄偰媍榑偟偨寢壥傪傆傑偊偰"悢"偺棟榑傪嶌偭偨偲偟偰傕偄傢備傞弞娐榑朄偵偍偪偄傞偍偦傟偼側偄偺偱偁傞丅傢傟傢傟偺擔忢惗妶偺拞偱偼偝傑偞傑側検偑尰傟偰偄傞丅傑偨暔棟妛摍偺宱尡壢妛偺傎偲傫偳偼偦傟偧傟撈帺偺検傪庢傝埖偭偰偄傞丅
丂偦偙偱検偵偮偄偰峫嶡偟偮偮"悢"偺棟榑傪憂傝忋偘傛偆偲偡傞偲偒庬乆偺崲擄偑偮偒傑偲偆偙偲偵側傞丅偙偺崲擄揰傪偺傝偙偊側偑傜悢偺棟榑傪揥奐偟偰備偔偨傔偵偼丄検偼宱尡彅壢妛偑柧傜偐偵偟偨傕偺偩偗傪峫嶡偟偰備偔偙偲偵偡傟偽傛偄丅偦偟偰偦偺検偺婎杮惈幙傪梫栺偟丄検偺奣擮傪柧妋偵掕媊偟偰偐傜丄偙傟偵婎偯偄偰尩枾側棟榑傪揥奐偟偰備偔偲傛偄偺偱偁傞丅
亂俁亃儐乕僋儕僢僪幃検偲帺慠悢
丂椺偊偽俀杮偺朹偺挿偝傪斾傋偰傒傛偆丅偳偪傜偑挿偄偐傪斾傋傞偲偒儊僕儍乕偼柍偔偲傕栚揑偼払偣傜傟傞丅傑偨俀恖偺恖暔偺恎挿傪斾傋偰傒傛偆丅偳偪傜偑恎挿偑戝偒偄偐偼儊僕儍乕偱應傜側偔偲傕傢偐傞敜偱偁傞丅偙偺傛偆側帠幚偼壗傪帵偡傕偺偱偁傠偆偐丅朹偺挿偝偲偐丄恎挿偲偐偼儊僕儍乕偱應傞偙偲偵傛偭偰偦偺懚嵼偑妋擣偝傟傞偲偄偆傕偺偱偼側偄偲偄偆偙偲傪帵偟偰偄傞偺偱偼側偐傠偆偐丅偮傑傝應傞慜偐傜丄應傞偲偄偆嶌嬈偲偼娭學側偟偵"挿偝"偲偄偆検偼懚嵼偟偰偄傞偲峫偊傜傟傞丅丂偦偙偱偁傜備傞挿偝傪慡晹廤傔傞偙偲傪峫偊偰傒傛偆丅偙偙偵侾庬偺廤崌偑偱偒傞偺偱偙傟傪俤偲昞傢偡偙偲偵偟傛偆丅廤崌E偺尦偼"挿偝"偱偁傞偑偙傟偼柍悢偵懚嵼偡傞丅偙傟傜傪俙丄俛丄俠丄丒丒丒摍偲昞傢偡偙偲偵偟傛偆丅乮俙丄俛丄俠丒丒丒偲偄偆挿偝偼儊僕儍乕偱應掕偝傟偰偄傞昁梫偼側偄丅乯棟榑偺慜採偲偟偰偺"挿偝"偲傛偽傟傞検偺婎杮惈幙傪柧傜偐偵偟偰偍偙偆丅揷懞棟榑偱偼師偺屲偮偺惈幙傪"挿偝偺岞棟"偲偟偰愝掕偟偰偄傞丅
丂丂岞棟嘥丂乮挿偝偺戝彫偵娭偡傞岞棟乯
丂丂岞棟嘦丂乮挿偝偺壛朄偵奐偡傞岞棟乯
丂丂岞棟嘨丂乮挿偝偺摍暘偵娭偡傞岞棟乯
丂丂岞棟嘩丂乮傾儖僉儊僨僗偺尨棟偲傛偽傟傞岞棟乯
丂丂岞棟嘪丂乮挿偝偺楢懕惈偵娭偡傞岞棟乯
亙岞棟侾亜
丂乮倝乯俙丆俛伕俤 側傜偽 俙亙俛丄俙亖俛丄俙亜俛 偺偆偪丄堦偮偩偗惉傝棫偮丅
丂乮鶤乯俙亙俛丄俛亙俠 側傜偽 俙亙俠偱偁傞丅
丂挿偝俙偺堦抂偵挿偝俛偺堦抂傪廳側傜側偄傛偆偵偮側偄偱堦偮偺挿偝傪嶌傞丅偙傟傪俀偮偺挿偝俙偲俛偺榓偲偄偄俙亄俛偲昞傢偡丅
亙岞棟嘦亜俙丄俛伕俤 側傜偽俙偵俛傪壛偊傞偙偲偑偱偒偰丄偦偺寢壥偲偟偰俙亄俛伕俤偑掕傑傞丅
丂俙丄俛丄俠伕俤偵懳偟偰
丂丂乮鶣乯俙亄俛亖俛亄俙
丂丂乮鶤乯乮俙亄俛乯亄俠亖俙亄乮俛亄俠乯
丂丂乮鶥乯俙亄俛亜俙 偑忢偵惉傝棫偮丅傑偨
丂丂乮鶦乯俙亙俛側傜傁俙亄倀亖俛偲側傞傛偆側倀伕俤偑偨偩堦偮懚嵼偡傞丅
丂丂丂丂乮鶦乯偐傜掕傑傞倀傪俛偲俙偺嵎偲偄偄丄俛亅俙偱昞傢偡丅
丂丂丂丂丂偙偺偲偒乮俛亅俙乯亄俙亖俛丄乮俛亄俙乯亅俙亖俛偑惉傝棫偮
丂偝偰亙岞棟俬亜乣亙岞棟嘪亜偺婎杮惈幙傪帩偮検偼挿偝偩偗偱側偔丄柺愊丄懱愊丄帪娫丄廳偝丄擬検丄摍偑偁傞丅偙偺傛偆側検傪儐乕僋儕僢僪幃検偲偄偄丄偦偺偲偒偺廤崌俤傪儐乕僋儕僢僪幃検嬻娫偲傛傇丅
丂偱偼儐乕僋儕僢僪幃検嬻娫俤偵偍偗傞曄姺偵偮偄偰峫偊偰傒傛偆丅
丂俙伕俤偺偲偒丂俙亄俙伕俤丄廬偭偰俙亄俙亄俙伕俤丒丒丒偱偁傞丅
丂丂倖丟俙丂仺丂俙亄俙丂丂丂乮倖乮俙乯亖俙亄俙乯
丂丂倗丟俙丂仺丂俙亄俙亄俙丂乮倗乮俙乯亖俙亄俙亄俙乯
丂丂丂丂丂丒丒丒丒丒丒
偺傛偆側曄姺偺廤崌偵偮偄偰峫偊傛偆丅倖乮俙乯亖俙亄俙側傞曄姺倖傪崱屻偼俀偲昞傢偟丄倗乮俙乯亖俙亄俙亄俙側傞曄姺倗傪俁偲昞傢偡偙偲偵偟傛偆丅傛偭偰俀乮俙乯亖俙亄俙丄俁乮俙乯亖俙亄俙亄俙丂偲側傞偑丄偙偺傛偆側俀丄俁丄丒丒丒傪攞曄姺偲傛傃丄攞曄姺偵傛傞憸偺俙亄俙丄俙亄俙亄俙丒丒丒摍傪俀俙丄俁俙丄丒丒丒摍偲昞傢偡丅廬偭偰倖乮俙乯亖俀乮俙乯亖俀俙丄倗乮俙乯亖俁乮俙乯亖俁俙丒丒丒偱偁傞丅偙偺傛偆偵偟偰堦斒偵攞曄姺丂値丟俙丂仺丂俙亄俙亄俙亄乧亄俙丂偑掕傔傜傟丄値乮俙乯亖値俙丂偲昞傢偡偙偲偑偱偒傞偺偱偁傞丅
丂傑偨峆摍曄姺倕丟俙丂仺丂俙丄乮倕乮俙乯亖俙乯偵懳偟偰丄偙偺倕傪侾偲昞傢偡丅偮傑傝侾乮俙乯亖俙偱偁傞丅埲忋偺傛偆偵偟偰掕傔傜傟偨攞曄姺侾丄俀丄俁丄丒丒丒丄値丄丒丒丒傪帺慠悢偲屇傇偺偱偁傞丅
丂偙偺傛偆偵掕媊偝傟偨帺慠悢偵偮偄偰偦偺惈幙偺堦抂傪挷傋偰傒傛偆丅侾乮俙乯亖俙丄俀乮俙乯亖俀俙亖俙亄俙丄偱偁傞偐傜丄侾丟俙丂仺丂俙丄俀丟俙丂仺丂俙亄俙偱偁傞丅
丂廬偭偰侾亄俀丟丂俙丂仺丂俙亄乮俙亄俙乯丄傑偨俀亄侾丟俙丂仺丂乮俙亄俙乯亄俙丅傛偮偰曄姺侾亄俀偲曄姺俀亄侾偲偼摍偟偄丅堦斒偵倎丄倐傪曄姺偲偟偰偺帺慠悢偲偡傞偲偒倎亄倐亖倐亄倎偱偁傞丅師偵俀丟俙丂仺丂俙亄俙偲俁丟俙丂仺丂俙亄俙亄俙偲偺崌惉偵偮偄偰峫偊偰傒傛偆丅俀乮俙乯亖俙亄俙亖俛偲偡傞丅
丂師偵俁乮俛乯亖俛亄俛亄俛亖乮俙亄俙乯亄乮俙亄俙乯亄乮俙亄俙乯亖俇俙偲側傞丅傛偮偰俁乮俛乯亖俁乮俀乮俙乯乯亖俁 俀乮俙乯亖俇俙丄傑偨俁乮俙乯亖俙亄俙亄俙亖俠偲偡傞丅
俀乮俙乯亖俇俙丄傑偨俁乮俙乯亖俙亄俙亄俙亖俠偲偡傞丅
丂師偵俀乮俠乯亖俠亄俠亖乮俙亄俙亄俙乯亄乮俙亄俙亄俙乯亖俇俙丄亪俀乮俠乯亖俀乮俁乮俙乯乯亖俀 俁乮俙乯亖俇俙丅廬偭偰曄姺俁
俁乮俙乯亖俇俙丅廬偭偰曄姺俁 俀偲俀
俀偲俀 俁偲偼摍偟偄丅偙偺傛偆偵偟偰丄崌惉曄姺倎
俁偲偼摍偟偄丅偙偺傛偆偵偟偰丄崌惉曄姺倎 倐偲倐
倐偲倐 倎偲偑摍偟偄曄姺偱偁傞偙偲偑傢偐傞丅幨憸堦斒偲偟偰偼倎
倎偲偑摍偟偄曄姺偱偁傞偙偲偑傢偐傞丅幨憸堦斒偲偟偰偼倎 倐亗倐
倐亗倐 倎偱偁傞偑帺慠悢偲偟偰偺曄姺偼倎
倎偱偁傞偑帺慠悢偲偟偰偺曄姺偼倎 倐亖倐
倐亖倐 倎偑惉傝棫偮丅岞棟嘨丄岞棟嘩丄傛傝桳棟悢偲偟偰偺曄姺丄峏偵偼岞棟嘪傛傝幚悢偲偟偰偺攞曄姺傪摫偒桳棟悢丄幚悢偺彅惈幙傪摫偔偙偲偑偱偒傞偑徻嵶偼師偺婡夛偵尒偰備偔偙偲偲偟偨偄丅
倎偑惉傝棫偮丅岞棟嘨丄岞棟嘩丄傛傝桳棟悢偲偟偰偺曄姺丄峏偵偼岞棟嘪傛傝幚悢偲偟偰偺攞曄姺傪摫偒桳棟悢丄幚悢偺彅惈幙傪摫偔偙偲偑偱偒傞偑徻嵶偼師偺婡夛偵尒偰備偔偙偲偲偟偨偄丅
丂嵞傃挿偝偵偮偄偰峫偊偰傒傛偆丅嬻娫偺拞偺俀揰俹丄俻偵偮偄偰偼俹偲俻偑堎側傞揰偱偁傟偽俹俻娫偺嫍棧偑掕傑傞丅偲偙傠偱俹丄俻偑堦抳偟偨応崌偼嫍棧偼側偄偺偩偐丆偙傟傕峀偄堄枴偱偺"挿偝"偲峫偊偰丄僛儘偺挿偝乮僛儘検乯偲柤偯偗侽偲昞傢偡偙偲偵偟傛偆丅儐乕僋儕僢僪幃検嬻娫俤偵偼偙偺傛偆側侽偼懚嵼偟側偄偺偱俤偵侽傪偮偗壛偊偨奼戝検嬻娫傪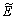 偲偟傛偆丅偦偟偰俙伕
偲偟傛偆丅偦偟偰俙伕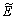 偲偟偰俙仺侽偲側傞曄姺傪悢侽偲柤偯偗傞丅
偲偟偰俙仺侽偲側傞曄姺傪悢侽偲柤偯偗傞丅
丂偮傑傝侽丟俙丂仺丂侽乮侽乮俙乯伕侽乯偱偁傞丅
丂傑偨値丟侽丂仺丂侽亄侽亄丒丒丒亄侽偱偁傞偐傜値乮侽乯亖値侽亖侽偱偁傞丅
亂係亃懳徧検偲懳徧検嬻娫
丂嬻娫撪偱偺暔懱偺堏摦偵偮偄偰峫偊偰傒偨偄丅偙偺"堏摦"偵偮偄偰偼擇偮偺峫偊曽偑偁傞丅堦偮偼弌敪揰偲摓払揰傪柧帵偟"揰俹偐傜揰俻傑偱"偲偄偆傛偆側帵偟曽偱偁傞丅傕偆堦偮偼弌敪揰偼偳偙偱傕傛偄偙偲偵偟偰"偙偺曽岦偵偙傟偩偗"堏摦偟偨偲偄偆帵偟曽偱偁傞丅偲偙傠偱曽岦偲偄偆尵梩傕擔忢惗妶偱偼擇捠傝偵梡偄傜傟偰偄傞丅堦偮偼"撿惣偺曽岦"偲偐"杒搶偺曽岦"偲偄偆傛偆偵岦偒偑巜掕偝傟偰偄傞応崌偱丄傕偆堦偮偼"搶惣偺曽岦""撿杒偺曽岦"偲偄偆傛偆偵岦偒偼巜掕偝傟偰偄側偄応崌偲偱偁傞丅崱屻"曽岦"偲偄偆偲偒偼岦偒傑偱巜掕偝傟偨堄枴偱梡偄傞偙偲偵偟丄"堏摦"偼"偙偺曽岦偵偙傟偩偗"偺堄枴偱梡偄傞偙偲偵偟傛偆丅偙偺偲偒堏摦偼桳岦慄暘偱帵偡偙偲偑偱偒傞偟丄婰崋偱偼 丄
丄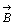 丄
丄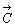 丒丒丒摍偱昞傢偡偙偲偵偟傛偆丅
丒丒丒摍偱昞傢偡偙偲偵偟傛偆丅丂崱  偺曽岦傪仮偱昞傢偟丄
偺曽岦傪仮偱昞傢偟丄 偺挿偝偼俙偲偡傞丅偙偺偲偒
偺挿偝偼俙偲偡傞丅偙偺偲偒  亖乮仮丄俙乯偲彂偔丅揰俹偐傜揰俻傊偺堏摦偲偄偆偲偒俹丄俻偑堎側傞偲偒偼
亖乮仮丄俙乯偲彂偔丅揰俹偐傜揰俻傊偺堏摦偲偄偆偲偒俹丄俻偑堎側傞偲偒偼 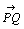 偱帵偡偙偲偑偱偒傞偑丄俹丄俻偑堦抳偡傞応崌偼埵抲傪曄偊側偄偙偲傪帵偡偐丄塣摦偺寢壥偲偟偰傕偲偺埵抲偵傕偳傞偙偲傪帵偡偺偱偙傟傕堦偮偺堏摦偲傒側偟"僛儘堏摦"偲屇傃
偱帵偡偙偲偑偱偒傞偑丄俹丄俻偑堦抳偡傞応崌偼埵抲傪曄偊側偄偙偲傪帵偡偐丄塣摦偺寢壥偲偟偰傕偲偺埵抲偵傕偳傞偙偲傪帵偡偺偱偙傟傕堦偮偺堏摦偲傒側偟"僛儘堏摦"偲屇傃 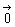 偱昞傢偡偙偲偵偟傛偆丅堦偮偺曽岦仮偵懳偟偰偼昁偢偦偺媡偺曽岦偑峫偊傜傟傞丅偙傟傪仮'偲昞傢偡偙偲偵偟傛偆丅傑偨堏摦
偱昞傢偡偙偲偵偟傛偆丅堦偮偺曽岦仮偵懳偟偰偼昁偢偦偺媡偺曽岦偑峫偊傜傟傞丅偙傟傪仮'偲昞傢偡偙偲偵偟傛偆丅傑偨堏摦  偲媡偺曽岦傪傕偪丄摨偠戝偒偝傪傕偮堏摦傪
偲媡偺曽岦傪傕偪丄摨偠戝偒偝傪傕偮堏摦傪 偺媡堏摦偲傛傃
偺媡堏摦偲傛傃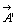 偱昞傢偡丅偙偺偲偒
偱昞傢偡丅偙偺偲偒  亖乮仮丆俙乯丆
亖乮仮丆俙乯丆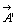 亖乮仮乫丆俙乯偱偁傞丅偙偺傛偆側堏摦偲偄偆検偼丄儐乕僋儕僢僪幃検偲偼堎側傞惈幙傪帩偭偰偄傞丅偦傟偼戝偒偝偺傎偐偵曽岦傪傕偮検偩偐傜偱偁傞偑丄挊偟偄摿旝偼丄偨偑偄偵媡偺曽岦偑懳偵側偭偰尰傟丄戝偒偝偑摍偟偔媡偺曽岦傪傕偮擇検偼偨偑偄偵徚偟崌偆偙偲偵偁傞丅揷懞擇榊巵偼偙偺傛偆側堏摦傪懳徧検偲柤偯偗丄堏摦偺廤崌傪懳徧検嬻娫偲傛傫偱偄傞丅懳徧検嬻娫傪側偡傕偺偼懠偵傕丄暯柺恾宍偺夞揮丄帪崗偺曄壔丄懍搙丄壛懍搙丄椡丄揹応丄帴応丄摍偑偁偘傜傟傛偆丅偙傟傜偺丄偳偺懳徧検嬻娫偵傕嫟捠偺婎杮惈幙傪梫栺偡傟傁丄偦傟偼懳徧検嬻娫偺岞棟偲偟偰愝掕偟偰傛偄偱偁傠偆丅
亖乮仮乫丆俙乯偱偁傞丅偙偺傛偆側堏摦偲偄偆検偼丄儐乕僋儕僢僪幃検偲偼堎側傞惈幙傪帩偭偰偄傞丅偦傟偼戝偒偝偺傎偐偵曽岦傪傕偮検偩偐傜偱偁傞偑丄挊偟偄摿旝偼丄偨偑偄偵媡偺曽岦偑懳偵側偭偰尰傟丄戝偒偝偑摍偟偔媡偺曽岦傪傕偮擇検偼偨偑偄偵徚偟崌偆偙偲偵偁傞丅揷懞擇榊巵偼偙偺傛偆側堏摦傪懳徧検偲柤偯偗丄堏摦偺廤崌傪懳徧検嬻娫偲傛傫偱偄傞丅懳徧検嬻娫傪側偡傕偺偼懠偵傕丄暯柺恾宍偺夞揮丄帪崗偺曄壔丄懍搙丄壛懍搙丄椡丄揹応丄帴応丄摍偑偁偘傜傟傛偆丅偙傟傜偺丄偳偺懳徧検嬻娫偵傕嫟捠偺婎杮惈幙傪梫栺偡傟傁丄偦傟偼懳徧検嬻娫偺岞棟偲偟偰愝掕偟偰傛偄偱偁傠偆丅
乻懳徧検嬻娫偺岞棟乼
亙岞棟俙亜丂懳徧検嬻娫俽偵懏偡傞擟堄偺擇偮偺検  丆
丆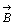 偐傜榓
偐傜榓  亄
亄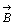 伕俽偑偨偩堦偮掕傑傞丅
伕俽偑偨偩堦偮掕傑傞丅
傑偨丄 丄
丄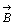 丄
丄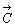 偵懳偟偰丄
偵懳偟偰丄
(鶣)丂 亄
亄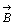 亖
亖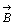 亄
亄 丂丂乮鶤乯乮
丂丂乮鶤乯乮 亄
亄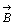 乯亄
乯亄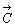 亖
亖 亄乮
亄乮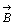 亄
亄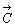 乯
乯
偑偮偹偵惉傝棫偮丅峏偵僛儘検偲傛偽傟傞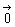 偑偁偭偰丄偳傫側
偑偁偭偰丄偳傫側  伕俽偵懳偟偰傕乮鶥乯
伕俽偵懳偟偰傕乮鶥乯 亄
亄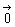 亖
亖 偑惉傝棫偮丅
偑惉傝棫偮丅
亙岞棟俛亜懳徧検嬻娫俽偐傜僛儘検傪彍偄偨巆傝偼丄曽岦廤崌俢偲堦偮偺儐乕僋儕僢僪幃検嬻娫俤偲偺捈愊俢亊俤亖乷乮仮丄俙乯乥仮伕俢丄俙伕俤乸偵傛偭偰昞傢偝傟傞丅偙偙偱摨曽岦偺擇検偵偮偄偰偼
乮鶦乯丂乮仮丄俙乯亄乮仮丄俛乯亖乮仮丄俙亄俛乯偑惉傝棫偮丅
傑偨擟堄偺曽岦仮伕俢偵懳偟偰丄仮偺媡曽岦仮'伕俢偑掕傑傝
乮鶧乯丂乮仮丆俙乯亄乮仮'丆俙乯亖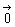 偑偮偹偵惉傝棫偮丅
偑偮偹偵惉傝棫偮丅
丂偱偼堦偮偺捈慄忋偱峴側傢傟傞堏摦傪峫偊偰偦偺廤崌傪俽偲偟傛偆丅偙偺応崌偺堏摦偵偼丄曽岦偼擇偮偟偐側偄丅偦偟偰偨偑偄偵媡偱偁傞丅偙偺応崌偺曽岦廤崌傪俢偲偡傞偲俢亖乷仮1丆仮2乸丄仮1'亖仮2丆偐偮仮'2亖仮1偱偁傞丅偙偺傛偆側俽傪倢師尦懳徧検嬻娫偲屇傇丅侾師尦懳徧検嬻娫俽偵偍偗傞曄姺偵偮偄偰峫偊偰傒傛偆丅 伕俽 偲偡傞偲偒
伕俽 偲偡傞偲偒  丂仺丂
丂仺丂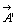 丂偺傛偆側曄姺傪亅侾偲掕媊偡傞丅
丂偺傛偆側曄姺傪亅侾偲掕媊偡傞丅
丂偮傑傝乮亅侾乯乮 乯亖
乯亖 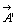 丂偱偁傞丅偙偺偲偒丂乮亅侾乯
丂偱偁傞丅偙偺偲偒丂乮亅侾乯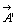 亖乮
亖乮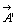 乯'亖
乯'亖 偲側傞丅
偲側傞丅
丂傛偭偰乮亅侾乯乮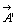 乯亖乮亅侾乯
乯亖乮亅侾乯 乮亅侾乯乮
乮亅侾乯乮 乯亖
乯亖  丆侾乮
丆侾乮 乯亖
乯亖 偁傞偐傜乮亅侾乯
偁傞偐傜乮亅侾乯 乮亅侾乯亖侾偲側傞丅偮傑傝媡曄姺傪偔傝曉偡偲峆摍曄姺偲側傞偙偲偐傜乮亅侾乯
乮亅侾乯亖侾偲側傞丅偮傑傝媡曄姺傪偔傝曉偡偲峆摍曄姺偲側傞偙偲偐傜乮亅侾乯 乮亅侾乯亖侾偑帵偝傟偨偺偱偁傞丅懳徧検嬻娫偵偍偗傞曄姺偵傛偭偰晧悢偺惈幙傪摫偒弌偡偙偲偑偱偒傞丅曄姺偺榓偼悢偺壛朄僿丄曄姺偺崌惉偼悢偺忔朄傊偲峫偊偰備偔偺偱偁傞丅
乮亅侾乯亖侾偑帵偝傟偨偺偱偁傞丅懳徧検嬻娫偵偍偗傞曄姺偵傛偭偰晧悢偺惈幙傪摫偒弌偡偙偲偑偱偒傞丅曄姺偺榓偼悢偺壛朄僿丄曄姺偺崌惉偼悢偺忔朄傊偲峫偊偰備偔偺偱偁傞丅
亂俆亃夞揮偵傛傞曄姺
丂暯柺忋偱偺恾宍偺夞揮偵偮偄偰峫偊偰傒偨偄丅検偲偟偰偺夞揮偵偼擇偮偺岦偒偑偁傝丄擇偮偺夞揮偼戝偒偝偑摍偟偔岦偒偑媡偱偁傞偲偒丄偙傟傜偺夞揮偼偨偑偄偵徚偟崌偆丅夞揮偺戝偒偝偼墌偺敿宎偲墌廃忋偺挿偝偲偺斾偱寛傔傞偙偲偑偱偒傞偑丄偙傟偑屖搙朄偺峫偊偱偁傞丅傑偨偙傟偼墌偺敿宎俼偵懳墳偟偰丄岦偒傪傕峫偊偨墌廃忋偺挿偝傪寛傔傞曄姺偱傕偁傞丅崱屻偼夞揮曄姺偲屇傇偙偲偵偟傛偆丅丂偦偟偰夞揮曄姺兤偵傛傝曽岦仮1偑曽岦仮2偵堏偝傟傞偲偒仮2亖仮1亄兤偲昞傢偡丅埥傞暯柺忋偺曽岦偺廤崌傪俢偲偡傞偲偒丄師偺偙偲偑偄偊傞丅
乮鶣乯夞揮兤偵傛傞俢偺曄姺仮仺仮亄兤偼慡扨幩偱偁傞丅
乮鶤乯夞揮兤1丆兤2偵傛傞曄専傪崌惉偡傟傁夞揮兤1亄兤2偵傛傞曄姺偲側傞丅
丂丂偮傑傝乹仮亄兤1乺亄兤2亖仮亄乮兤1亄兤2乯偱偁傞丅
乮鶥乯俢偺峆摍曄姺仮仺仮偼夞揮侽丄亇俀兾丄亇係兾丆丒丒丒丂偵傛偭偰傂偒婲偙偝傟傞丅
乮鶦乯擟堄偺仮1丆仮2伕俢偵懳偟丄仮1亄兤亖仮2偲側傞兤偑懚嵼偡傞丅
乮倴乯夞揮兤亖兾偼曽岦偺懳徧曄姺傪傂偒婲偙偡丅仮亄兾亖仮'
丂埲忋偺乮倝乯乣乮倴乯偼暯柺偺婎杮惈幙偲偟偰擣傔偰傕傛偄偟丄暯柺偺曽岦廤崌傪摿挜偯偗傞傕偺偲偄偭偰傕傛偄丅懳徧検嬻栤俽偺曽岦廤崌偑偙偺惈幙傪傕偮偲偒俽傪俀師尦懳徧検嬻娫偲傛傇丅偦偟偰暯丂柺偵偍偗傞夞揮兤偼検嬻娫俽偺曄姺傪傂偒婲偙偟丄兤丟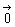 丂仺丂
丂仺丂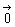 丄傑偨
丄傑偨  亗
亗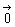 偺偲偒
偺偲偒  亖乮仮丆俙乯偲偡傞偲兤丟乮仮丆俙乯仺乮仮亄兤丆俙乯偲側傞丅
亖乮仮丆俙乯偲偡傞偲兤丟乮仮丆俙乯仺乮仮亄兤丆俙乯偲側傞丅
亂俇亃俀師尦懳徧検嬻娫偲暋慺悢
丂暋慺悢偲偼壗偐丅懡偔偺恖偼暋慺悢偺寁嶼朄傪抦偭偰偄傞偑丄暋慺悢偺堄枴偵偮偄偰偼昁偢偟傕柧妋偵攃埇偟偰偄傞傢偗偱偼側偄丅拪徾悢妛傛傝摫偐傟傞暋慺悢偺棟榑偼偐側傝擄夝側撪梕傪帩偭偰偄傞丅崱変乆偼検嬻娫偵偍偗傞曄姺偲偟偰悢傪掕媊偡傞偲偄偆棫応偵棫媟偟偰偄傞丅偙偺傛偆側棫応偐傜偼暋慺悢偲偼偳偺傛偆偵掕媊偝傟傞偺偱偁傠偆偐丅偦偺慜偵暋慺悢偺堄枴傪柧傜偐偵偡傞偵偼偳偺傛偆側偙偲偑柧傜偐偵偝傟側偗傟偽側傜側偄偺偐偵偮偄偰峫偊偰傒傛偆丅偦傟偼師偺嶰揰偵傑偲傔傜傟傛偆丅丂乮鶣乯倝2亖亅侾偲側傞嫊悢扨埵倝偲偼壗偐丅
丂乮鶤乯倐偲倝偺愊倐倝偲偼壗偐丅
丂乮鶥乯倎偲倐倝偲偺榓偲偐壗偐丅
丂埲忋傪検嬻娫偵偍偗傞曄姺偲偟偰峫偊偰偄偭偰傒傛偆丅
丂俀師尦懳徧検偺戙昞偲偟偰暯柺儀僌僩儖傪偲傝丄偦偺慡懱傪俽偲偡傞丅崱丄 伕俽 偱
伕俽 偱 亖乮仮丆俙乯偲偡傞丅
亖乮仮丆俙乯偲偡傞丅 偵兾/俀偺夞揮曄姺傪巤偡偲
偵兾/俀偺夞揮曄姺傪巤偡偲 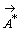 亖乮仮亄兾/俀丆俙乯偲側傞丅偦偙偱師偺傛偆偵掕媊偡傞丅
亖乮仮亄兾/俀丆俙乯偲側傞丅偦偙偱師偺傛偆偵掕媊偡傞丅
丂暯柺儀僋僩儖偺曄姺 丟 仺
仺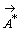 傪嫊悢扨埵偲偄偄倝偱昞傢偡丅廬偭偰倝乮
傪嫊悢扨埵偲偄偄倝偱昞傢偡丅廬偭偰倝乮 乯亖
乯亖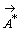 亖倝
亖倝 偲側傞丅廬偭偰倝偲偼"暯柺儀僋僩儖傪俋侽亱夞揮偡傞"偙偲偱偁傞偲峫偊偰傛偄丅師偵倐倝偲偼擇偮偺曄姺倝偲倐偲偺崌惉偱偁傝丄倎亄倐倝偲偼擇偮偺攞曄姺倎偲倐倝偲偺榓偱偁傞丅
偲側傞丅廬偭偰倝偲偼"暯柺儀僋僩儖傪俋侽亱夞揮偡傞"偙偲偱偁傞偲峫偊偰傛偄丅師偵倐倝偲偼擇偮偺曄姺倝偲倐偲偺崌惉偱偁傝丄倎亄倐倝偲偼擇偮偺攞曄姺倎偲倐倝偲偺榓偱偁傞丅
丂偱偼曄姺倝偺廳梫惈幙傪摫偄偰傒傛偆丅
丂  亗
亗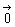 偺偲偒
偺偲偒  亖乮仮丆俙乯偲偡傞丅偙偺偲偒倝偲倝偺崌惉曄姺傪峫偊偰傒傛偆丅
亖乮仮丆俙乯偲偡傞丅偙偺偲偒倝偲倝偺崌惉曄姺傪峫偊偰傒傛偆丅
倝 倝乮
倝乮 乯亖倝乮倝乮
乯亖倝乮倝乮 乯乯亖倝乮
乯乯亖倝乮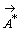 乯亖乮仮亄兾/俀亄兾/俀丆俙乯亖乮仮亄兾丆俙乯亖乮仮'丆俙乯亖
乯亖乮仮亄兾/俀亄兾/俀丆俙乯亖乮仮亄兾丆俙乯亖乮仮'丆俙乯亖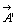 亖乮亅侾乯乮
亖乮亅侾乯乮 乯丂丂亪倝
乯丂丂亪倝 倝亖亅侾偲側傞丅俀師尦懳徧検曄娫偵偍偗傞曄姺偵傛偭偰暋慺悢倎亄倐倝偵娭偡傞彅惈幙傪摫偔偙偲偑偱偒傞偑丄偙傟偼暿偺婡夛偱庢傝埖偆偙偲偵偟傛偆丅
倝亖亅侾偲側傞丅俀師尦懳徧検曄娫偵偍偗傞曄姺偵傛偭偰暋慺悢倎亄倐倝偵娭偡傞彅惈幙傪摫偔偙偲偑偱偒傞偑丄偙傟偼暿偺婡夛偱庢傝埖偆偙偲偵偟傛偆丅
 俀乮俙乯亖俇俙丄傑偨俁乮俙乯亖俙亄俙亄俙亖俠偲偡傞丅
俀乮俙乯亖俇俙丄傑偨俁乮俙乯亖俙亄俙亄俙亖俠偲偡傞丅 俁乮俙乯亖俇俙丅廬偭偰曄姺俁
俁乮俙乯亖俇俙丅廬偭偰曄姺俁 俀偲俀
俀偲俀 俁偲偼摍偟偄丅偙偺傛偆偵偟偰丄崌惉曄姺倎
俁偲偼摍偟偄丅偙偺傛偆偵偟偰丄崌惉曄姺倎 倐偲倐
倐偲倐 倎偲偑摍偟偄曄姺偱偁傞偙偲偑傢偐傞丅幨憸堦斒偲偟偰偼倎
倎偲偑摍偟偄曄姺偱偁傞偙偲偑傢偐傞丅幨憸堦斒偲偟偰偼倎 倐亗倐
倐亗倐 倎偱偁傞偑帺慠悢偲偟偰偺曄姺偼倎
倎偱偁傞偑帺慠悢偲偟偰偺曄姺偼倎 倐亖倐
倐亖倐 倎偑惉傝棫偮丅岞棟嘨丄岞棟嘩丄傛傝桳棟悢偲偟偰偺曄姺丄峏偵偼岞棟嘪傛傝幚悢偲偟偰偺攞曄姺傪摫偒桳棟悢丄幚悢偺彅惈幙傪摫偔偙偲偑偱偒傞偑徻嵶偼師偺婡夛偵尒偰備偔偙偲偲偟偨偄丅
倎偑惉傝棫偮丅岞棟嘨丄岞棟嘩丄傛傝桳棟悢偲偟偰偺曄姺丄峏偵偼岞棟嘪傛傝幚悢偲偟偰偺攞曄姺傪摫偒桳棟悢丄幚悢偺彅惈幙傪摫偔偙偲偑偱偒傞偑徻嵶偼師偺婡夛偵尒偰備偔偙偲偲偟偨偄丅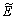 偲偟傛偆丅偦偟偰俙伕
偲偟傛偆丅偦偟偰俙伕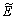 偲偟偰俙仺侽偲側傞曄姺傪悢侽偲柤偯偗傞丅
偲偟偰俙仺侽偲側傞曄姺傪悢侽偲柤偯偗傞丅 丄
丄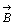 丄
丄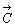 丒丒丒摍偱昞傢偡偙偲偵偟傛偆丅
丒丒丒摍偱昞傢偡偙偲偵偟傛偆丅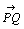 偱帵偡偙偲偑偱偒傞偑丄俹丄俻偑堦抳偡傞応崌偼埵抲傪曄偊側偄偙偲傪帵偡偐丄塣摦偺寢壥偲偟偰傕偲偺埵抲偵傕偳傞偙偲傪帵偡偺偱偙傟傕堦偮偺堏摦偲傒側偟"僛儘堏摦"偲屇傃
偱帵偡偙偲偑偱偒傞偑丄俹丄俻偑堦抳偡傞応崌偼埵抲傪曄偊側偄偙偲傪帵偡偐丄塣摦偺寢壥偲偟偰傕偲偺埵抲偵傕偳傞偙偲傪帵偡偺偱偙傟傕堦偮偺堏摦偲傒側偟"僛儘堏摦"偲屇傃 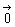 偱昞傢偡偙偲偵偟傛偆丅堦偮偺曽岦仮偵懳偟偰偼昁偢偦偺媡偺曽岦偑峫偊傜傟傞丅偙傟傪仮'偲昞傢偡偙偲偵偟傛偆丅傑偨堏摦
偱昞傢偡偙偲偵偟傛偆丅堦偮偺曽岦仮偵懳偟偰偼昁偢偦偺媡偺曽岦偑峫偊傜傟傞丅偙傟傪仮'偲昞傢偡偙偲偵偟傛偆丅傑偨堏摦 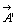 偱昞傢偡丅偙偺偲偒
偱昞傢偡丅偙偺偲偒 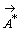 亖乮仮亄兾/俀丆俙乯偲側傞丅偦偙偱師偺傛偆偵掕媊偡傞丅
亖乮仮亄兾/俀丆俙乯偲側傞丅偦偙偱師偺傛偆偵掕媊偡傞丅