北海道苫小牧東高等学校　　矢嶋　裕之

はじめに

第１章 本稿が『完結編』とならなかった経緯について

第２章　検証１：指導要領の比較について

　昭和２６年（１９５１年）に文部省から改訂版として出版された中学校高等学校学習指導要領の数学科編（試案）の『第�V章　中学校数学科の一般目標と指導内容　§２　中学校数学科の指導内容（３７ページ）』 に『生活経験』についての定義とも言える部分がある。次は原文をそのまま引用したものである。

第�V章　中学校数学科の一般目標と指導内容　§２　中学校数学科の指導内容 　中学校の数学科の一般目標を達成するために、教師が実際の指導を計画するとき、何をとりあげて指導したらよいかを、まず考えねばならない。このとりあげるべきものをさして、指導内容といっている。それならば、指導内容とはどんな性格のものか。これを、次に考えてみよう。 　人間は、自分が積極的に参加して経験したことからのみ、その経験を一般化して、次の経験に対処する方法を学ぶ。このことは、生徒が、前に述べたような能力や理解を身につけていくときにも同様である。すなわち、数学が有効に用いられる、あるいは新しい数学が必然的に必要となるような場面に生徒が遭遇し、そこにおける問題を生徒が積極的に解決していく過程において、教師が、いろいろ必要な援助を与え、その解決ができるようにしていくとき、生徒は、目標とするような一般化を生み出すのである。このときに注意すべきことは、その解決を経験することに、目標に対して有意義な数学的な面を含み、しかもその数学が、目標にあるように社会的に有意義にきいていることである。 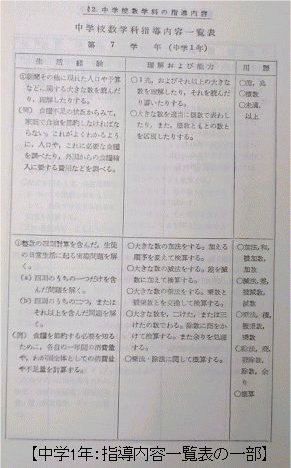　このような経験を名づけて、生活経験とよぶならば、数学科の指導内容は、このような生活経験によって組織されなければならないといえよう。すなわち、生徒は、この生活経験をとおして、一般目標の方向に発達していく。教師は、生徒が次々に一般化して生み出すことが、うまく累積していくように、この生活経験を与えなければならない。 　生活経験から生まれる一般化が、うまく累積していくように計画を立てるにはどうしたらよいであろうか。 　このような経験として適当なものの具体的な系列は、地域によって、また生徒個人によって、いろいろと違っているものであることはいうまでもない。特に、数学は、きわめて応用の広いものであるから、これを含む経験として、これがよくて、あれが悪いということは、全国一律にはなかなかいいうるものでない。ここに、数学科の具体的な指導計画が、教師各人の責任にゆだねられているゆえんがある。 　この教師の責任を遂行するための手がかりとなる参考資料として考えられたものが、次にあげる指導内容一覧表である。すなわち、望ましいと考えられる生活経験を、ある観点から類型に分け、この類型を大ざっぱな生徒の発達に沿って配列した参考見本が、この指導内容一覧表である。 　この類型を分ける観点としては、一般化され累積されていくもの、すなわち、数学的な内容によるのが至当であろう。そして、その数学的な内容がうまく累積していくように、すなわち、生徒の発達の段階に沿って、学年に配当することが必要となる。次にあげる指導内容一覧表は、このような考えのもとにつくられたものである。 　これをもとにして、教師が指導計画を立てるときに注意すべきことをあげてみると、次のようになる。 ここに分類してあるのは、生活経験の類型である。実際にとりあげるものは、その例としてあげてあるような具体的な経験である。 理解および能力と用語の欄にあげてあるのは、このような経験から一般化されて出てくるだろうと予想されるものである。実際にあるひとつの経験をとりあげたとき、これらのすべてが出てくるとは限らない。 それゆえ、具体的な経験の系列を計画していくときには、この表は、ひとつのチェックリストとガイドの役目をなすものである。この表にあげてある番号の順に、各番号にひとつずつの経験をあげていけば、それで済むというものではない。 学年の程度は、全国的にみて、普通の生徒が普通に学習してだいたいこの程度にいけるであろうと予想されている程度にしてある。この程度までは、だれでも到達しなければならないというような強い基準ではない。このような基準は、各個人個人によって異なるものであるし、しかも、その異なるものは、 現在までの研究の段階では、はっきり決められるだ けの根拠をもたない。 経験の例としてあげてあるものは、それ自身の意味のほかに、一方においては、このようなことから一般化される程度にという意味で、右側にあげてある一般化の程度を示している。 この表は、各学年でとりあげる経験のおもな分野を示したものともいえる。その内容を流れる数学的な発達については、第�W章を参考せられたい。

（２）高等学校数学科『一般数学』（昭和２６年）について

　次節にあげる今回の新しい学習指導要領の高等学校数学科の『数学基礎』ときわめて類似性が高いのが次にあげる昭和２６年当時の高等学校数学科の『一般数学』に関する記述部分である。高等学校数学科の『各科目の性格』も添えて次に引用したい。

第�X章　高等学校数学科の各科目の一般目標と指導内容 §１．各科目の性格 どうして、高等学校で数学が選択必修になっているか。（省略） 科目を分けるにあたって、どのようなことを考慮しなければならないか。（省略） 現在数学科では、どのように科目を分けているか。 科目のまとまりをつけていく観点として、大ざっぱに考えて、次のふたとおりの性格を考えている。その一つは、将来それほど数学を必要としない生徒に対して、一般的教養という立て前から、中学校の学習を発展させたものである。一般数学がこれにあたる。その二は、将来数学を必要とする生徒、あるいは、数学をもっと深く学習したい生徒に対し、その必要と関心に基いて分けた科目である。 解析�T・解析�Uと幾何とに分ける観点としては、次のような考え方をとっている。すなわち、数学の分野として、生徒に考えられる分け方は、数量関係を問題としていく面と、図形的な関係を問題としていく面とである。生徒の関心は、主としてこのような面に分化してくる。解析�T、解析�Uは前者にあたり、幾何は後者にあたる。 数量的な関係を問題にしていく面では、その第一の段階として、函数を大局的にそのグラフや式の形によってとらえ、これに必要な計算を行っていくものと、このような見方をさらに発展させ、いろいろな問題に応用して規則性をとらえたり、函数そのものについて微小変化や極限を考えてさらにつきこんだ見方をしたりしていくものとが考えられる。この前者にあたるものが解析�Tであり、後者は解析�Uにあたる。したがって、解析�Uは解析�Tに引き続いて学習されるべきものである。 図形的な関係を問題にしていくのは、幾何である。幾何では、図形的な関係を問題として、これに対する方法として論証的な見方や解析的な見方を発展させる。 上のように分けた場合、いちばん気をつけなければならないことは、次のことである。これらの科目は、いずれも数学的な考え方を学ぶ点では共通なものであって、その問題の所在や必要な程度によってのみ分けたものである。したがって、その目標や指導内容においては、たぶんに共通なものを含んでいるようにしなければならない。 §２．一般数学の一般目標と指導内容 〔一般目標〕 数学の応用の広いことや、数学が文明の進歩の上に果たしている役割について理解し、数学に対する関心を深める。 日常生活で当面する実務や消費生活について、数量的な観察をして問題を構成する能力や、その解決に必要な数学的な知識技術を身につけるとともに、それらを用いる習慣を養う。 いろいろな関係を簡単めいりょうに表わすものとして、また、問題解決にあたっての有力な道具として、数学を理解し、数学的な記号や操作を用いる能力を養う。 簡単な図形の性質を知り、それらが実際的な問題の解決にあたって果たしている役割を理解し、これを用いて、新しい問題を解決していく能力を養う。 論理的な考え方の本質と必要とを理解し、筋道を立てて、論理的に考えていく習慣を養う。 数量的な処理をしていくときに、数値の正しさや、それに対する制限を考えていく習慣を養う。特に、統計的な資料のとり方、整理のしかた、解釈のしかたについての理解を深めるとともに、物事を誤りなくとらえたり、正しく伝えたりする能力と、統計的な考え方を社会生活で正しく用いる態度とを養う。 一般数学の指導内容 指導内容を、生活経験によってあげたのは、中学校の場合と同じ趣旨によっている。これについては、３７ページを参照せられたい。 ここにあげているのは、指導内容の一例であって、生徒の能力や必要に応じて、ある事がらを省くとか、つけ加えるとかなどして指導してよいことは、いうまでもない。 指導にあたっては、これらの生活経験を豊かに含んだ生徒の問題をとりあげ、この問題の解決をとおして、これらの数学的な内容を身につけていくことができるようにすることが望まし い。これについては第�Y章を参照せられたい。

　注：上の記述（引用部分）における『３７ページ』とは前節（１）で引用した部分である。

　大学時代に学んだ教職科目『教育原理』のレクチャーノートでも日本における学習指導要領の変遷については記述が大変多かった。中でも戦後の学習指導要領は改訂などを繰り返すにつれてコンパクト化が進んできている。そして、『学習指導要領』とは別に『学習指導要領解説』というものも出版されるようになり、現在に至っている。昭和２６年に出版された学習指導要領は現在のものに比べるとかなり厚く、ちょうど現在の『学習指導要領解説』も併せ持った感じである。そして、この当時の単元についての構成の仕方や大切な点については昭和２６年に出版された学習指導要領では事細かに述べられていた。これらの点は当時の『生活単元学習』でどのようにして教師が教えていたかを知る大切な手がかりとなる。そのため、次章以降でまとめることとする。

　

　

（３）今回の学習指導要領における高等学校数学科『数学基礎』の記述について

　さて、今回新しく出された学習指導要領の中で高等学校『数学基礎』はどのように記述されているのだろうか。次は、『数学基礎』に関する記述部分のすべてである。

高等学校指導要領　第４節　数学　第２款　各科目　　　　（平成１１年３月） 第１数学基礎 １　目標 　数学と人間のかかわりや、社会生活において数学が果たしている役割について理解させ、数学に対する興味・関心を高めるとともに、数学的な見方や考え方のよさを認識し数学を活用する態度を育てる。 ２　内容 （１）数学と人間の活動 　数量や図形についての概念等が人間の活動にかかわって発展してきたことを理解し、数学に対する興味・関心を高める。 ア　数と人間 イ　図形と人間 （２）社会生活における数理的な考察 　社会生活において数学が活用されている場面や身近な事象を数理的に考察することを通して、数学の有用性などを知り、数学的な見方や考え方を豊かにする。 ア　社会生活と数学 イ　身近な事象の数理的な考察 （３）身近な統計 　目的に応じて資料を収集し、それを表やグラフなどを用いて整理するとともに、資料の傾向を代表値を用いてとらえるなど、統計の考え方を理解し、それを活用できるようにする。 ア　資料の整理 イ　資料の傾向の把握 ３　内容の取扱い （１）内容の（１）については、数学における概念の形成や原理・法則の認識の過程と人間や文化とのかかわりを中心として、数学史的な話題を取り上げるものとする。 （２）内容の（２）については、社会生活と数学とのかかわりの身近な事例を取り上げるよう配慮するものとする。 （３）内容の（３）については、統計の基本的な考えを扱うものとし、また、コンピュータ等を活用した学習がなされるよう配慮するものとする。 （４）この科目の指導に当たっては、身近な事例を取り上げるなど生徒が主体的に学習できるようにし、理論的な考察には深入りしないよう配慮するものとする。

第３章　単元による学習指導のねらいについて

　生活単元学習が現在の学習とどのように違うものなのか、この章では昭和２６年の中学校高等学校学習指導要領の第�Y章より引用する形でまとめてみた。

第�Y章　数学科における単元による学習指導§１．単元による学習指導のねらい

◆単元でとりあげる問題を解決していく過程は、書かれた問題を解決していく過程と比べて、どんな点に相違があるか。
　この相違点は次の事例で示すように問題文を見れば一目瞭然に区別できる。
Ａ．こづかいをどのように使ったらよいか。
Ｂ．こづかい１５０円を毎月もらっているこどもがある。その４０％を本代の予算に割り当てたとすると、毎月の予算は何円になるか。

１．問題の把握について
Ａ．なぜそのことが問題となるのかということ、すなわち、その理由となることが、こどもたちの生活の中にあり、こどもの必要に基いたものである。問題を解決していくためには、このなぜということを、こどもたち自身で考えなければならない。
Ｂ．なぜということは、教師がおもにこどもたちのことを考えて、説明して与える。このような形で問題を与えれば、あるこどもは必要を感ずるし、他のこどもは感じないかもしれない。なぜということを考えなくとも、問題は解ける。

　Ａのような問題を解決していくためには、なぜこづかいを問題にするのか、そのわけをはっきり考えなければならない。そうすると、ほしいものが買えないとか、むだづかいをしすぎて困ったとか、いろいろなこどものトラブルがまず考えられるだろう。そして、なぜそのトラブルが困ったことになるのか、その理由を反省していけば、自主的に消費生活を規正していって、りっぱな中学生としての生活をしていきたいというような、こどもの必要につきあたるであろう。
　こうした必要をはっきり自覚して、これを分析していってこそ、この問題が解決されるのである。
　Ｂのような問題では、このなぜは教師の考えた数学の指導過程の中の一つの手段にすぎず、こどもたちの生活の中から題材は取ってはいるが、生活を高めようとする点が反省されてないから、このなぜの生まれる理由がない。たとえそれが反省されたにしても、問題が特定の状態のものに限定されているから、すべての生徒が、その必要を感ずるとはいえない。たとえば、毎月定額のこづかいをもらっていない生徒は、この問題にそれほど必要を感じないであろう。また、本代の予算をどうして４０％ときめたのかわからないから、本を買うことにあまり重きをおいていない生徒は、なぜそんなことをするのかわからないであろう。また、こづかいを豊かにもらっている生徒は、何も予算などたてなくてもよいではないかと考えて、この問題にあまり必要をおぼえないかもしれない。また、こうしたことを教師がていねいに説明して必要をおぼえさせたとしても、また次の問題について、同じようなことをくり返さなければならない。

２．問題の分析について
Ａ．この問題を解決していくためには、さきにあげたなぜということをよく考えて、問題を分析し たり、限定したりして、Ｂのように数量的に解決できるいくつかの問題に分析していかなくてはならない。
Ｂ：この問題を解決していくためには、問題のなかにある条件に基いて、与えられた数量の間の数量的関係を明らかにし、どんな計算や測定などを適用すればよいかを考えればよい。解決のために必要な仮定や資料はいっさい与えられている。

《解説省略》

３．解決の多様なことについて
Ａ：分析のしかた、限定のしかたは必ずしも一義的でない。したがって、分析や限定のしかたに応じて、いろいろな程度の一連の問題が起こってくる。解決も同一の結果にはならない。
Ｂ：解決のためにとり出される関係は、一義的である。その関係の処理のしかたには、いろいろな方法が考えられても、結果は同一になる。

《解説省略》

４．解決の限界について
Ａ：得られる結果は、自分できめた仮定や条件に基くものであるから、それが実際にどんな意味をもっているか、どんな限界をもっているかがめいりょうになるし、まだどんなことが残されているかも明らかになる。
Ｂ：仮定や条件がどうして生まれたかが明示されていないから、その結果を実際の生活の上にどう適用してよいかがはっきりしない。

《解説省略》

◆単元による指導はどんなことをねらっているのか。 要点のみをあげると次のようになる。

1. 数学を用いて、生活を改善し続けてやまない人間の育成をねらっている。
2. 自主的に学習していくこどもの育成をねらっている。
3. 個人差に応じて問題を解決しながら、しかも、みんなが協力して仕事をしていく人間の育成をねらっている。
4. 今までに得た能力を用いて問題を構成することや、既習の技能の用い方を適宜に指導していくことをねらっている。

　以上、昭和２６年の学習指導要領より引用したが、この章をさらに簡潔にまとめると次のようになる。

（１）単元による学習指導は、次の点で書かれた問題解決による指導と違った面をもっている。
�@なぜそれが問題となるかを考える。
�Aそこから問題の分析や限定が必要となる。
�B分析・限定のしかたによって、いろいろな問題が一連として起る。
�C解決されたものとされないものとの区別が明らかになる。

（２）単元による学習指導は、次のことをねらっている。
�@（１）の�@�Cの特徴から、数学を用いて、生活を改善し続けてやまない人間の育成をねらっている。
�A（１）の�@�Aの特徴から、自主的に学習していくこどもの育成をねらっている。
�B（１）の�@�Bの特徴から、個人差に応じて問題を解決しながら、しかも、みんなが協力して仕事をしていく人間の育成をねらっている。
�C（１）の�@�A�Bの特徴から、既習の能力を用いて問題を構成することや、既習の技能を適宜に指導していくことをねらっている。

第４章　単元を構成するときの留意点と学習指導上の留意点について

　第３章でまとめたように、昭和２６年頃は生活経験に基づく『生活単元学習』が展開されたが、この単元による学習指導のねらいに合うように単元を構成するときにどんな点に留意したのであろうか。同じく、昭和２６年の学習指導要領では次のように謳っている。

◎数学を用いて、生活を改善し続けてやまない人間の育成をねらうためには、どんなことに留意して単元を構成したらよいか。

1. 取りあげるものについて
   （a）社会から見ても、こどもから見ても、有意義であるとともに、それらの必要に答えるものであること。
   （b）問題を限定して、問題の焦点を明らかにすることのできるものであるとともに、今後の研究がさし示されるものであること。
   （c）数学が問題解決の焦点に対する判断のかぎを握っているものであること。

2. 取りあげる問題の契機について
   （a）自分の思考や行動を、いっそう正確にするために。
   （b）自分の思考や行動を、いっそう能率的にするために。
   （c）自分の思考や行動を、いっそう的確にするために。
   （d）自分の思考や行動を、いっそう気軽にできるようにするために。

3. 取りあげる数学的内容について
   　その数学的内容−技能−が生活を改善していくのに重要な役割を果していくことがわかるようなものであること。

◎自主的に学習していくこどもの育成をねらっていくためには、単元を構成するときに、どんなことに留意したらよいか。

1. 取りあげるものについて
   （a）こどもの必要や興味をもとにし、これらを伸ばし続けていくものであること。
   （b）こどもに、解決できたときの喜びがある程度予期できるものであること。
   （c）こどもが解決しうる希望をもてるものであること。
   （d）こどもの当面しているトラブルや困難をとりあげたものであること。また、必要に応じて、そのトラブルや困難をこどもに印象づけて、問題の解決に向けていくことのできるものであること。

2. 取りあげる数学的内容について （a）こどもが努力しさえすれば克服していける程度の困難度があり、こどもが成功感を味うことのできるものであること。
   （b）新しい原理・法則・規約・用語・記号などが一般化しやすいように、言い換えると、抽象化しやすいようになっていること。
   （c）新しい原理・法則・規約・用語・記号などが、既習のものとどんな関係があるかが明らかになるようになっていること。
   （d）新しい原理・法則・規約・用語・記号うなどとまぎらわしいものがあるとき、これを比べやすいようになつていること。

◎個人差に応じ、問題を解決しながら、しかもみんなが協力して仕事をしていく人間の育成をねらっていくには、どんなことに留意したらよいか。

1. 取りあげるものについて
   （a）こどもの生活面における個人差に応じて、問題を取りあげることのできるものであること。
   （b）ひとつのテーマのもとに、能力に応じて問題を取りあげることのできるものであること。
   （c）どんな取りあげ方をしても、そのテーマに対して、すべてのこどもが貢献することが明らかなものであること。

2. 取りあげる数学的内容について
   （a）問題を解決するにも、その解決を一様に限定することをしないで、いろいろな手法が考えられるようにすること。
   （b）取りあげるものに、なんらかの意味で同じ面があるようになっていること。

◎既習の技能を適宜に指導していくことをねらうには、どんなことに留意したらよいか。

1. 取りあげるものについて
   （a）問題を構成するときに、既習のものが用いられるものであること。
   （b）特に、こどもの困難を感ずるものに対しては、問題の解決に際して、指導の機会のあるものであること。

　では、学習指導するにあたっての留意点は何だったのであろうか。

◎数学を用いて、生活を改善し続けてやまない人間の育成をねらうためには、どんなことに留意して学習指導をしたらよいか。

1. 数学が思考や行為を改善していくのに有用なものであることを明らかにする。
   （a）数学を用いると、思考や行為がいっそう正確になることを、生徒が確認できるようにすることに指導の重点をおく。
   （b）数学を用いると、思考や行為がいっそう能率的になることを、生徒が確認できるようにすることに指導の重点をおく。
   （c）数学を用いると、思考や行為がいっそう気軽にできるようになることを、生徒が確認できるようにすることに指導の重点をおく。
   （d）数学を用いると、思考や行為がいっそう的確になることを、生徒が確認できるようにすることに指導の重点をおく。

2. 生活を改善していく面がまだあることを明らかにする。
   （a）問題の解決は、一応の解決であって、暫定的なものであることを生徒にわからせる。
   （b）問題が解決されると、生活面からみても、数学面からみても、まだ解決しなければならない問題が残されていることを生徒にわからせる。
   （c）どれだけのことがわかって、まだどれだけのことがわからないかを生徒に確認させる。

3. 技能を反復復習して、生徒の身につけ、いつでも必要に応じて適用できるようにすることがたいせつであることを明らかにする。
   （a）技能を正確に適用できるようにすることに指導の重点をおく。
   （b）定められた技能を、はやく行うことができるようにすることに指導の重点をおく。

4. 問題を解決するときに、これをいくつかの問題に分析し、その問題の解決をとおして、もとの主要問題が解決できるかどうかを反省するように指導する。

◎自主的に学習していく生徒の育成をねらっていくためには、どんなことに留意して学習指導をしたらよいか。

1. 解決の方法よりも、解決しなければならない理由や解決しなければならない事がらが重要であり、後者によって前者が定まるものであることを明らかにする。
2. 生徒の当面しているトラブルや困難がどんなところに原因があり、また、これらは何によって克服できるかを明らかにするとともに、必要に応じて、学習の場を単純化したものに置き換えて、その場の構造を明らかにし、問題を構成しやすいようにしてやる。
3. 今までに学習したものに比べて、どんなところを、どんなに改善したらよいかがわかるようにする。こうして、生徒に目標がはっきりつかまるようにする。
4. 問題の解決ができたら、どんなに望ましい生活ができるようになるかを明らかにする。
5. 生徒の能力に応じた努力に対して、ほめてやる。しかも、成功したかどうかが生徒に確認できるようにする。
6. 失敗しても、これをけなすようなことをせず、これを生かして、次の学習に役だてるようにする。
7. 生徒のたてた計画などを、できるだけ尊重してやる。
8. 生徒に自分のわかったことを発表する機会を、豊富に準備してやる。
9. 展示物や見学などを利用して、生徒が進んで学習していくように環境を整える。

◎個人差に応じ、問題を解決しながら、しかも、みんなで協力して仕事をしていく人間の育成をねらっていくには、どんなことに留意して学習指導をしたらよいか。

1. 各生徒の解決している問題が、取りあげている主要問題とどんな関係にあるかを明らかにする。
2. グループ研究を進めて、これをうまくまとめて主要問題の解決に導くようにする。

◎技能を適宜に指導していくことをねらうためには、どんなことに留意して学習指導をしたらよいか。

1. 生徒が、今までにもっているものを用いて問題を構成するように指導し、生徒の能力をいっそう高めるようにする。
2. 各生徒について、どんなところが弱くて、どんなところが強いかを見定めて、指導のねらいを各生徒に応ずるようにする。
3. 各生徒について、どんなところに伸びる可能性をもっているかを見いだすように努める。
4. 生徒の誤りを早期に発見して、指導の時期を失わないようにする。

　第３章と第４章にわたって、生活単元学習について、単元をどのように設定し、どのように点に注意しつつ学習指導していったかを、そのほとんどを昭和２６年の学習指導要領からの引用を中心にしてまとめた。この年の学習指導要領には、さらに、単元ごとの指導計画のたて方や評価の仕方などについても詳細な記述があり、それらを読めば読むほど、現在でも立派に通用するものだと感じられるようになってきた。ただ、本研究はこの『生活単元学習』についての研究ではなく、新科目『数学基礎』の教材事例をめぐるものであるので、『生活単元学習』についてのさらなる研究はまた別の機会にまわし、３本目となった本稿を閉じたいと思う。

おわりに

　本稿は、そのほとんどが昭和２６年に発行された中学校高等学校学習指導要領数学科編（試案）の復刻版ともいえる巻末にあげた参考文献からの引用となった。そのため、特に第３章から第４章にかけての部分で抜き書きとなった部分が多く、論文作成時の項目番号の起こし方のルールに合わない表記が目に付く形となってしまった。これは、原文についている番号などの表現を変えずに引用したため起きたのだが、脱稿してみると何とも読みにくい。従来、引用物が多いレポートを書くことはほとんどなかったため、これを契機に論文作成の方法を再度勉強し直そうと考えている。

　『生活単元学習』時代の実際の教科書の画像ファイルを整理する作業もかなり進み、あと少しで終了する予定である。次回こそ、このシリーズの一応の完結編となるように作業を進めたいと考えている私であった。

平成１２年７月９日

• 文部省学習指導要領７巻〜８巻算数科数学科編日本図書センター昭和５５年
• 高等学校学習指導要領文部省平成１１年３月