教材余話（１）

数学基礎『数の表記法』をめぐって

北海道苫小牧東高等学校　矢嶋　裕之

はじめに

　『情報』や『数学基礎』など新しい学習指導要領で初めて登場する教科や科目の教科書の白表紙本や各種資料が最近になってやっと私の元にも届き始めた。その中でも『数学基礎』は以前私が仮説を立てたように昭和２０年代後半の『生活単元学習』の頃の『数学一般』の一部の教科書と類似性が見られた。これらのことについては後日まとめる予定だが、『数学基礎』で『数の表記法』についてかなりのページ数を割いて数学史との関連も示唆しながら述べられていることに興味をもった。その単元を私が生徒に教えるとしたらどのように展開させるか、このレポートを書き出したきっかけはここにあった。本稿は、教室でインターネットを手軽に利用できる設定の下でバーチャルな授業の組み立てについての一考察である。

第１章 まずは説明する

（１）教室の環境に合わせたやり方を

　教科書と黒板しか使えない教室では教科書とチョークを使って授業をするしかないが、インターネット接続端末が教室にある場合は、例えば『神聖文字』などキーになる単語の情報検索してどんなサイトがあるのかなとど教科書という枠を越えた活動が可能だと思われる。また、たとえ、教室にインターネット用のコンセントがついていなくても、学校にハンディなプロジェクターさえあれば、ノート型パソコン１台とプロジェクターを使って追体験的にインターネットの利用事例を見せることもできる。まずは教室の環境に合わせた授業の方法を取り入れたいものです。

（２）教授する方法の改善

　インターネットを利用するかどうかはともかく、まずは教科書を使って簡単に内容を説明しないとなりません。ただ、これまでの授業ではこの『教授』の部分にほとんどの時間をとられていました。その教授の方法ですが、教科書を生徒に読ませたり、あるいは、教科書にある例題を黒板を使って説明する。こんな従来の教授の仕方を変えてみませんか。たとえば、教科書の内容をパワーポイントで作っておいて、プレゼンテーションの要領で講義を進める（もちろん、生徒にもスライドを印刷した資料は与えておいて）ことは多分どこの学校でもできることだと思います。また、パワーポイントには音声データを貼り付ける機能も付いていますからうまく使えば出張中にも授業（講義）に穴をあけることなく（ただし、パソコンを操作してもらう代理の先生は必要になると思いますが）授業を進めることも可能だと思います（これは私がテストパターンを考えているのですが）。説明はなるべく簡単にして、前述のように部分的にインターネットで情報検索していくつかのサイトを見るというのも効果的であると思います。ただし、これは生徒の動機付けという側面が強いため、あまり時間をかけない方がいいと思います。パソコンやインターネットの授業での利用で困るのはそれらの利用が目的になってしまうような使い方です。パソコンやインターネットは単なるツールにすぎないので『何のために使うのか』を授業者は常に明確にしておく必要があります。生徒の動機付けのために『神聖文字』のサイトを見せていたらそれだけで１時間が終わってしまった、そんなことだけは避けたいものです（かなり注意しないとそうなりがちです！）。

第２章　『調べ学習』を課題にする

　これまでの教科書と異なり、某出版社の『数学基礎』の教科書（の白表紙本）の場合、従来の『例』と『問』という形態以外にも問題に取り組む姿勢の違いを少しずつ変えて様々なアプローチを用いている。これは扱うレベルの差はあるものの広範囲な意味での『調べ学習』である。教科書がこのようになってきているのであれば、なおさら『調べ学習』のきっかけはつかみやすい。以下では、『数の表記法』の事例について私のバーチャルプランを紹介したいと思う。

（１）教科書に載っていない『数の表記法』を調べる

　ちょっとインターネットを利用するだけでたくさんの『数の表記法』が過去あったことがわかります。検索エンジンを利用すれば、これらについて初心者でもいろいろなサイトに入って調べることができ、それらを加工してまとめることもできます。ここではスペースの関係から、私が短時間で調べることのできたもののうち一部を紹介したいと思います。まだ他にもたくさんあるはずです。

【くさび型文字】（右の図）
　左列は１から９までと１０，２０，３０，４０，５０を表し、右列は左列の９倍した数を表している。従ってアのところは１８０を意味している。

【古代エジプト】（下の図）

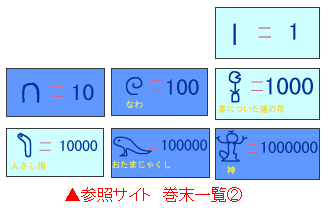
【マヤ文明】
　この時代は碑文の中だけでも数字の表し方が４通りの方法がある。最も一般的なものは点と棒による表記である。右の図のように点は１を表し、棒が５を表す。また、０（ゼロ）は貝の象形文字で表される。また、この他にも頭字体による数の表現方法もあるが、これはどういう仕組み（単に１から１９までを数しかない、つまり２０進法、のか）なのかよくわからない。ただ、高度な数学術があったとされるマヤ文明について調べるのであれば、やはり、天文学と関連させて取り組ませるのも１つの方法かと思われる。

（２）小数や分数の表記法

　数の表記法については、当然のことながら分数や小数の表記法がどうなっているのかという問題も残る。整数と違って関連性のあるサイトが短時間ではうまく見つからなかったが、現代の表記法と異なるものが多いのも事実である。そして、１６世紀末頃のステヴィンの小数記号やバビロニア（６０進法）で使われていた小数の表記法は、かなり独特のものである。

（３）『数の表記法』から『足し算』へ

　関連した学習事項としてすぐ考えられるのは足し算である。足し算についてはある程度関連するサイトが見つかった。このように教科書の内容をふくらませていけばいろいろな発展が考えられる。

（４）最後はプレゼンテーション

　せっかく調べ学習をさせるのだから最後は発表で締めくくりたいものである。パワーポイントで作品を作ったり、ホームページビルダーで作品を作ると見栄えのよいものが容易に作れる。ワープロソフトでも最近では画像ファイルを容易に貼り付けられるから、紙面発表でもいいから何らかの形にまとめさせて、一連の学習を締めくくるのが好ましいと思う。

第３章　数学関連ホームページ

ＹＡＨＯＯ！をはじめとするたくさんの検索エンジンを使えば、無限大にあるインターネットのサイトから必要とするサイトなどを容易に探せる。しかし、かなりうまく検索作業をしないと検索結果のサイトが多すぎて実際的とはいえない。そういう場合、数学関連（あるいは情報教育関連）のホームページを利用するという方法もある。岩手県立大学市川尚先生が作ったサイト
　（http://www.anna.iwate-pu.ac.jp/~ichikawa/new/9903.html）
に次のような数学関連のものがあった。詳細は下記のＵＲＬに入って利用していただければわかると思われるので、ここではそのＵＲＬと名称だけを記載しておく。

  1. http://www.nikonet.or.jp/spring/『数学のいずみ』
  2. http://web.kyoto-inet.or.jp/people/haselic/『一数学教師のこだわり』
  3. http://www.yukichi.ne.jp/~firefly1/ 『なるほど・ザ・数学』
  4. http://moon.ap.kyushu-u.ac.jp/~math/『数学史とMathematical Wonderland』
  5. http://www2.gunmanet.or.jp/mow/『MOWMOWMOW』
  6. http://www2.nkansai.or.jp/users/yoshioka/『ちょっと真面目な数学教員』
  7. http://www.wcsnet.or.jp/~miyaguti/『Mathmatical Trip』
  8. http://wwwnj.aichi-edu.ac.jp/suugaku/sugakuindex.htm『愛知教育大学附属名古屋中学校数　学科ホームページ』
  9. http://www.ies.co.jp/math/『Math Education and Technology』
  10. http://www.nsknet.or.jp/~y_aoki/『数学の部屋』
  11. http://www.ajhs.wakayama-u.ac.jp/『和歌山大学教育学部付属中学校』
  12. http://www.fuzoku.okayama-u.ac.jp/ml/Welcome.html『岡山教育大学付属岡山中学校』
  13. http://www.saga-ed.go.jp/materials/edq01447/index.htm『MATH-GATE』
  14. http://www.mnet.or.jp/~ujino/『MatheMagics』
  15. http://www.mahoroba.or.jp/~fukagawa/『数学の丘』

おわりに

　この半年間、大正時代の教育史、一言で言うならば『大正デモクラシー下における教育』について調べている。先の『リバイバル論』を書いていた時期には第２次世界大戦以降の日本の教育だけを扱っていたのだが、さらに『生活単元学習』を調べていくうちに大正時代の教育も調べることになってしまったのだ。ところが、そのテーマはそう簡単にまとめられるものではなく、いつ頃になったら書き出すことになるのか自分でも見当がつかない。一方、『はじめに』でもふれたように新しい教科や科目の白表紙本をやっと見られるようになり、まとめられる題材からまとめたというのが現在の私である。本稿で取り上げた『表記法』は学生時代にも調べたことがなく、大学時代（実際の私は純粋数学を嫌い、サンプリング調査やデータ解析の方ばかりをやっていたのだが）にもっと数学や数学教育に関した勉強や研究をしておけばよかったと後悔している。本稿であげたバーチャルプランは今はバーチャルであるが、何とか実際にやってみたいと考えている。しかし、本校をとりまく『大学受験』というものを考えると実現のめどは大変厳しく、実現のために時間を作り出す必要性を強く感じている。本稿では『数の表記法』についての考察であったが、次回は円周率πについてまとめる予定である。
１２月１０日（月）
卒業式実行委員会の生徒を指導しながら脱稿する

参考サイト（第２章関係）

①http://www23.big.or.jp/~lereve/tuugaku/47.html
②http://math.edu.mie-u.ac.jp/~kanie/stidents/nyoko/ejiputo.htm
③http://www.y-asakawa.com/tansaku-report/report-mexico1.htm