教材余話（４）

最短径路問題とビリヤードと

北海道苫小牧東高等学校　矢嶋　裕之

はじめに

『身近な事象の数理的考察』、これは以前私が教科書すら持ってこない生徒が大半を占めていた学校勤務時代に暗中模索していた研究テーマの１つであった。このテーマそのものがいくつかの教材事例とともに『数学基礎』の教科書（白表紙本）に載っていた。本稿は前作までの３本と同様に『数学基礎』の教科書をもとに、教科書で扱われている内容を発展展開していく方法の一例を紹介するものである。今回は、前述した『身近な事象の数理的考察』の中で取り上げられていた最短径路問題（単に距離が最短）を取り上げ、ビリヤードへの応用を紹介するという普通の内容である。具体的な内容を構築していく際に利用したのは前回までと同様にインターネットのみである。最短径路問題そのものよりはビリヤードに関する記述の方が多くなると思うが、コーヒーブレークにお読みいただければ幸いである。


第１章　最短径路（距離としての）問題とは

　参考にさせていただいた『数学基礎』の教科書（白表紙本）では、多くの方が愛車に装着しているナビゲーターシステムの挿し絵（写真）が使われていたが、一般的なイメージとしては理解できるが、道路の混み具合（混雑状況）という情報がインプットされないタイプが多いので、これは現実的な最短径路（この場合は時間という物差し）を示すものとは言えないように思う（注：私自身、ナビゲーターシステムを利用していないため、正しい記述ではないかもしれないが）。また、数学的に『最短径路』という場合には、このような俗世間的な要因を一切排除して単なる距離が最短な径路を示す、そういう前提でこれ以降は書くこととする。

　さて、教科書等でよく描かれている問題例としては、『点Ａを出発して途中で点Ｐを通り、さらに点Ｂまでいく場合の最短径路』という設定である。そして、これはよく次のようなまとめがなされている。
『ＡＰ＋ＰＢの最短』
直線ｌについて、点Ａと対称な点をＡ’とする。直線Ａ’Ｂとｌとの交点をＰとすると、点Ａからｌ上の点を通って点Ｂにいたる最短の径路は点Ｐを通る。

　このように考えることによって私たちは単純な最短径路問題ならすぐ解ける。しかし、こうした基本内容を活用したり発展させたりするといろいろな問題を作ることができる。その代表にあげられるのが次章でふれるビリヤードを用いたものである。


第２章　ビリヤードの仕方で最も単純な部分だけを使った問題例

　タイトルがくどくなったのには理由がある。ビリヤードを実際に趣味としてやっている方ならよくわかっていると思われるが、単なる玉突きにすぎないビリヤード（と書くと、専門家の方に申し訳ないが）も大変奥の深い世界である。私情になって申し訳ないが、私の勤務校では毎年２～３月頃に冬の教職員レクとして室内種目のレクレーションを実施している。私が本校に赴任した６年前には、碁・将棋・麻雀・ボーリングといった種目であったが、３年前、私が数学科の幹事をしていた時からビリヤードを加えてもらった。別にビリヤードがうまいとかではなく（ちなみに私は種目によらず運動が弱い）、勝負にこだわらず皆と親睦を深めるにはボーリングのように実力差の歴然としたものではなく、誰が勝つか負けるか不透明な種目の方が親睦が深まると考えていたわけである（ちなみに、初めてやった私が初年度優勝してしまった、若い頃から趣味の一つとしてやっていて当然優勝するはずの先生がいたのに。でも２年目は実力通りに最下位、この年の準優勝はこれまた初めてやった教頭先生）。それ以降、年に１回だがビリヤードを楽しんでいる。キュー（突く棒のこと）で手玉（自らが突く白い玉のこと）を突くにあたっても突く部分により手玉にいろいろな回転が加わり、ひねりが加えられることができるので必ずしも手玉は直線的に回転（進展）するとは限らない。このような実際的な話を全て排除して以下では教科書で扱われているように①玉は直線を描いて回転し、②外側の枠で跳ね返って（光が鏡に反射するときと同様に入射角と反射角が等しく）最短の径路を通る、ものとして記述を進めるものとする。まずはビリヤードの基本的な例からふれようと思う。

【例１】手玉Aをクッション（外側の枠のこと）のどこかでバンクする（跳ね返す）。

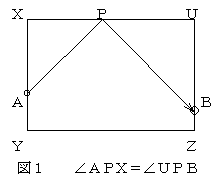
【例２】手玉Ａを先球（狙う対象の玉のこと）Ｂにクッションにバンクさせてあてる。
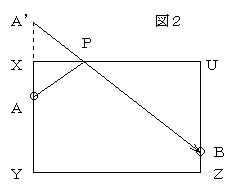
　この場合、クッションのどこの辺でバンクさせるか、これこそ前述の最短径路の問題そのものである。図２のように、手玉Ａの位置と点Ｘについて対称な点Ａ’とし、Ａ’ＢとＸＵの交点Ｐを狙ってストローク（キューの反復運動）すると点Ｐでバンクして手玉Ａは先球Ｂにあたる。

　ここからが本章の本題となる。

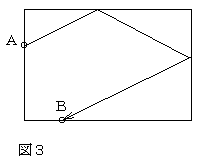
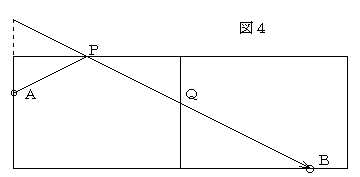
【例３】今度は手玉Ａは同じ場所で、先球Ｂの場所をＹＺ上の点とする。（なお、以下では前提として直線的に狙うのではなく、必ずクッションで何度かバンクさせて狙うものとする、この部分も以下では省略するが）理屈とすれば図３のように２点ＰとＱでバンクすればよい。ではＰとＱはどんな点になるのか。実はこれは図４のようにすればよいのである。

　

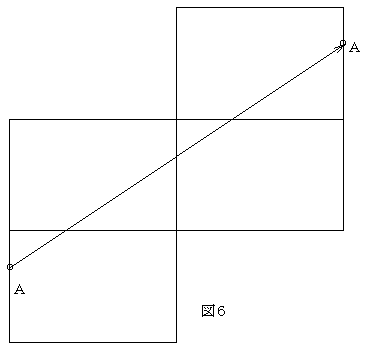
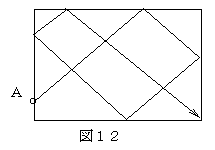
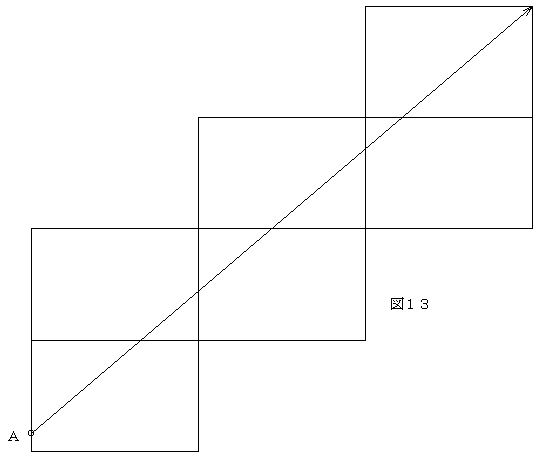
【例４】手玉をクッションに３回バンクさせてテーブル（ビリヤードの台のこと）を１周させて元の位置に戻す。これは、図６のように３回バンクさせて戻すことである。

　

　ここまでは、参考にした教科書にもあったものである。さて、普通、私たちがビリヤードをする場合は、テーブルにポケット（ビリヤードの台にある穴のこと）がついたものを使ったポケットビリヤードが主流を占めます。以下では、ポケットビリヤードでの応用例です。

【例５】バンクショット
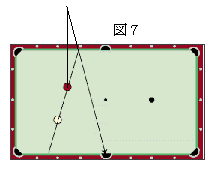
　先球をポケットに入れる場合、手玉をどこに置くかという事例です。右の図７のように置けばうまくいきます。【例２】の応用です。

【例６】ファイブ　アンド　ハーフ
　本来はファイブハーフシステムというクッションのシステムの１つで、コーナーポケットの前から対角の２．５ポイントの地点を突くと反対のポケットに手玉が向かうことになっています。撞点（手玉の突く場所）によってかなり違いが出るなどいろいろあるのですが、本稿ではそれらを全て排除して単純に最短径路として考えています。次のような径路をたどれば、うまくいきます。

　　

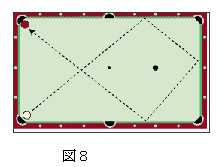
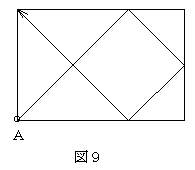
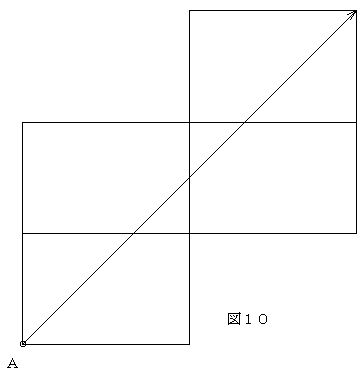
【例７】二重回し
　ファイブ　＆　ハーフを２つ組み合わせたシステムで、５回クッションするので結構ハデです。これも本来は、撞点などいろいろテクニック的なことがあるのですが、ここでは全て光の反射原理だけで考えることにします。

　　

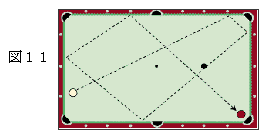
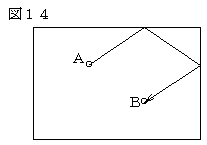
【例８】テーブル上の２玉
　クッションなどに接していない２つの場所に手玉Ａと先球Ｂがある場合、どうすれば手玉Ａが先球Ｂにあたるか考えます（もちろん、直線的には狙わない）。この場合は次のように例３を応用させて２回クッションさせて最短径路をたどればあたります。

　　

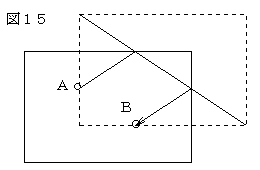
　さて、以上は実際のビリヤードの仕方の細かい部分を一切排除して単純なルール（光の反射の原理）にして考えたものです。ですから、実際のビリヤードでもこうなるとは限りません（と言うより、そうはいかないと思います）。ただ、最短径路問題を扱うのであれば、少し脱線してこのように扱ってみるのもよいのではないでしょうか。また、運動量保存の法則など物理の教材としてビリヤード等を扱うのもおもしろいと思われます。


おわりに

　本稿を書き終わって『やはり………』となってしまった。何かというと『ビリヤードの内容しか書いていない』ということである。本稿を数学の先生ばかり集まる真面目な研究会である『数学実践研究会』に持ち込んでいいのか、とも。『まあ、まだ正月中であるし………』と理由にならない理由をこじつけて脱稿してしまった次第である。
　今年はどうしたわけか、元旦の昼から各種レポートを書き始めてしまい、夕食は家族と一緒に実家（といっても自宅から車で１０分）で３世代揃って食べたものの、朝から夕方までの日中は書斎に閉じこもっての生活となってしまった。加えて、１月５日からは当初４月１日から開始するはずだった禁酒（禁ビール）生活を３ヶ月前倒しで始めてしまった。私にとって今年はどんな年になるのであろうか。
　さて、ビリヤードの原則的な部分のみを用いて書いた本稿だが、ワープロ入力時に思わぬところに時間がかかってしまった。それは、ビリヤードの最短径路問題同様な展開図の作成部分であった。私は普段『一太郎』を使ってレポート作成しているが、最初、書き上がった原稿をＨＴＭＬ化してみたら、図のところが抜けてしまっていた。ワープロ入力と印刷だけであれば問題にならないことなのだが、Webにまとめる時に問題になるので、図の部分だけを別処理して（お絵かきソフトなどを使って）後で貼り付けて完成させようとしたができなかった（正確には、自分がイメージしたようには仕上がらなかった）。ワープロソフトの機能高度化や周辺ソフトの充実に感謝しながらも、自分のイメージした通りにいかないのは何とも歯がゆいものである。
　さて、次のレポートでは『身近な統計』の教材の発展のさせ方について扱う予定です。

１月７日（月）　脱稿する

参考にしたサイト