アポロニウスの円

定義を少し広げる試み

愛知県立高浜高等学校　　　山崎　博司

１．はじめに

　「数研通信」 (No .33) に次のようなことが載っていた。

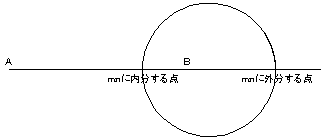
「２つの定点Ａ，Ｂからの距離の比が"ｍ：ｎである点の軌跡がアポロニウスの円であるが、その中心は線分ＡＢをm2:n2に外分する点である。」

　証明は、アポロニウスの円が図のように線分ＡＢを m:n に内分する点と外分する点を直径の両端とすることから、中心の座標（それらの中点)を計算すればよい。　（神奈川県湘南高校 石濱文武先生）

　このことの別証を示したいと思う。

２．内容

　予備知識として次の２つの（１）,（２）を確認しておく。

（１）点(x, y)が円外のとき、
　　f(x, y)=(x - a)2 +(y - b)2 - r2
　は(x, y)から円 f(x, y) =0 にひいた接線の長さの２乗を表す。

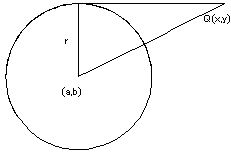
（２）２つの円
　　f (x, y)=(x - a1)2+(y - b1)2-r12=0
　　g (x, y)=(x - a2)2+(y - b2)2-r22=0
に対して、方程式
　　s f (x, y) + t g (x, y) =0
は円 (または１点、虚円)を表し、
　　その中心は線分ABをt:sにわける点
である。
　ただし、f(x,y)=0、g(x,y)=0の中心をそれぞれA,Bとする。
とくにst<0のときは必ず円になる。
　（「方程式sf(x,y)+tg(x,y)=0の表す図形」参照）

　さて、２点A(a1,b1),B(a2,b2)を中心とする２つの円
　　f(x,y)=(x-a1)2+(y-b1)2-r12=0
　　g(x,y)=(x-a2)2+(y-b2)2-r22=0
を考える。
　これら２つの円までの接線の長さの比がm:nになる点の軌跡の方程式は
　　f(x,y)/m2=g(x,y)/n2
である。だから
　　n2f(x,y)-m2g(x,y)=0
となる。
　これは円を表し、
　　その中心は線分ＡＢを(-m2):n2に分ける点、つまり　m2:n2に外分する点
である。
　ここで２つの円f(x,y)=0,g(x,y)=0の半径を限りなく０に近づければ、できあがり。

［まとめ］

　上の方程式
　　n2f(x,y)-m2g(x,y)=0
つまり
　　　m2{(x-a1)2+(y-b1)2-r12}-m2{(x-a2)2+(y-b2)2-r22}=0
は、もとの２つの円までの接線の長さの比がm:nになる点の軌跡であり、円を表す。そしてその中心は線分ＡＢをm2:n2に外分する点である。
　とくに
　　r1=mk、r2=nk　(k∈R)
のとき、アポロニウスの円に一致する。
（つまり２定点Ａ，Ｂからの距離の比がm:nである点の軌跡になっている。）

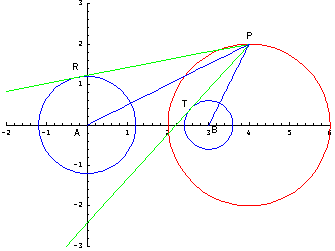
(∵)上の図で、r1=mk、r2=nkであるとき△PRAと△PTBは相似である。だから
　　PA/PB=PR/PT=m/n