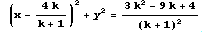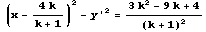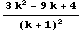lは、l1とl2の交点をとおる直線を表し、その方向は次のようになっている。
l1,l2,lの法線ベクトルをそれぞれ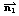 ,
,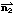 ,
,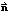 とすると
とすると
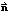 =s
=s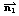 +t
+t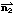
である。
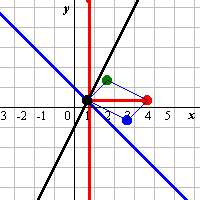 [具体例1−(1)]
[具体例1−(1)]
l1:f(x,y)=2x-y-1=0
l2:g(x,y)=x+y-1=0
に対して
l:f(x,y)+k・g(x,y)=0
を図示する。
lはl1,l2に平行な直線を表し、a1=a2,b1=b2としておけば2直線l1,l2からの距離の比がt:sになるような位置にある。
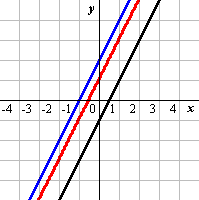 [具体例1−(2)]
[具体例1−(2)]
l1:f(x,y)=2x-y-1=0
l2:g(x,y)=2x-y+2=0
に対して
l:f(x,y)+k・g(x,y)=0
を図示する。
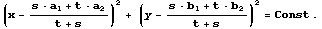
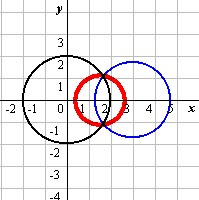 [具体例2−(1)]
[具体例2−(1)]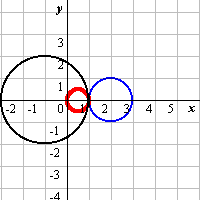 [具体例2−(2)-a](外接)
[具体例2−(2)-a](外接)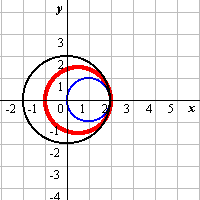 [具体例2−(2)-b](内接)
[具体例2−(2)-b](内接)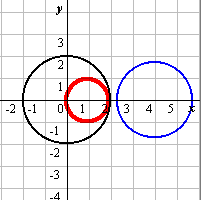 [具体例2−(3)]
[具体例2−(3)]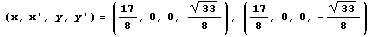
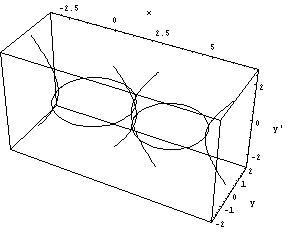 4次元では図示が困難なので、「x'=0における切り口」(3次元)のグラフを考える。
4次元では図示が困難なので、「x'=0における切り口」(3次元)のグラフを考える。