2次方程式の解について

「実係数の２次方程式の解は虚数解のときは共役な２数なのに実数解のときそうでないのはなぜか」

　以下では
　　ｚ＝ａｘ²＋ｂｘ＋ｃ＝０　(ａ≠０)
また、
　　 ｘ→ｘ＋ｙｉ，ｚ→ｚ＋ｗｉ　　ｘ，ｙ，ｚ，ｗ∈Ｒ
とおきかえる
すると、この2次関数は
　　(ｘ，ｙ)→(ｚ，ｗ)
という対応だから、グラフは４次元の図形になる
それを視覚的に表わすことには無理があるので
　　ｚ＝ｆ(ｘ，ｙ)，　　ｗ＝ｇ(ｘ，ｙ)
のグラフをを別々に描いてみる
２次方程式
　　ａｘ²＋ｂｘ＋ｃ＝０
の解は、ｚ＝０ かつ ｗ＝０ となるような(ｘ，ｙ)である
そのような点(ｘ，ｙ)は2つのグラフを照合すればわかるであろう

（１）　ｘ²−４ｘ＋５＝０　虚数解の場合

 
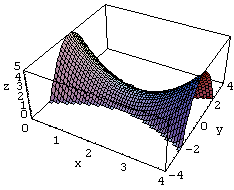
z=Re[(x+y I)^2-4 (x+y I)+5] 
Plot3D[z,{x,0,4},{y,-4,4}, 
  PlotRange->{0,5},PlotPoints->50, 
  ClipFill->None,AxesLabel->{"x","y","z"}]; 

 
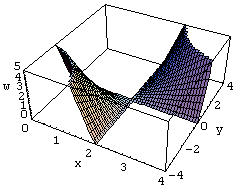
w=Im[(x+y I)^2-4 (x+y I)+5] 
Plot3D[w,{x,0,4},{y,-4,4}, 
  PlotRange->{0,5},PlotPoints->50, 
  ClipFill->None,AxesLabel->{"x","y","w"}]; 

（２）　ｘ²−４ｘ＋４＝０　重解の場合

 
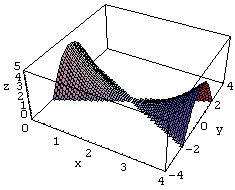
z=Re[(x+y I)^2-4 (x+y I)+4] 
Plot3D[z,{x,0,4},{y,-4,4}, 
  PlotRange->{0,5},PlotPoints->60, 
  ClipFill->None,AxesLabel->{"x","y","z"}]; 

 
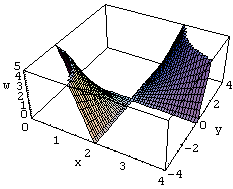
w=Im[(x+y I)^2-4 (x+y I)+4] 
Plot3D[w,{x,0,4},{y,-4,4}, 
  PlotRange->{0,5},PlotPoints->50, 
  ClipFill->None,AxesLabel->{"x","y","w"}]; 

（３）　ｘ²−４ｘ＋３＝０　異なる2つの実数解の場合

 
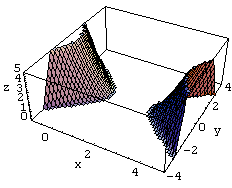
z=Re[(x+y I)^2-4 (x+y I)+3] 
Plot3D[z,{x,-1,5},{y,-4,4}, 
  PlotRange->{0,5},PlotPoints->50, 
  ClipFill->None,AxesLabel->{"x","y","z"}]; 

 
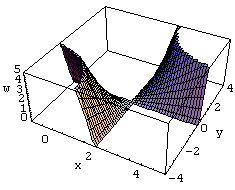
w=Im[(x+y I)^2-4 (x+y I)+3] 
Plot3D[w,{x,-1,5},{y,-4,4}, 
  PlotRange->{0,5},PlotPoints->50, 
  ClipFill->None,AxesLabel->{"x","y","w"}]; 

以上のことから、2次方程式の解は

ｘ−ｙ平面上における双曲線と 2直線の交点（重解の場合は、2直線と 2直線の交点）

ｚ＝ａｘ²−ａｙ²＋ｂｘ＋Ｃ　より
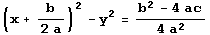　　　　・・・(ａ)　双曲線
ｗ＝(２ａｘ＋ｂ)ｙ＝０　より
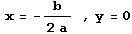　　　　・・・(ｂ)　2直線
つまり２つの図形 (a),(b)の交点が解である