 いろいろな形をした同じ高さの滑り台があります。各滑り台の最高地点からボールを転がすと,どのボールがより速く地面に到達するでしょうか。斜面の長さは,直線状の滑り台が一番短いのですが,結果はどうなるでしょうか?
いろいろな形をした同じ高さの滑り台があります。各滑り台の最高地点からボールを転がすと,どのボールがより速く地面に到達するでしょうか。斜面の長さは,直線状の滑り台が一番短いのですが,結果はどうなるでしょうか?この作品は,以下の"最速降下問題"と呼ばれる問題を題材に製作されました。
最速降下問題:
鉛直面に与えられた2点間を曲線で結び,その曲線に沿って質点を滑り落とす。最も短い時間で滑り落ちる曲線を求めよ。
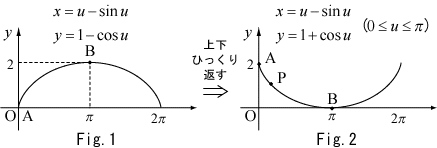
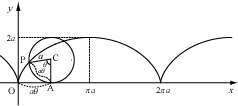 この問題は,ヨハン・ベルヌーイやライプニッツなどによって解かれ,その答えは直線でも円弧でもなく,サイクロイド曲線と呼ばれる曲線です。(*)1 サイクロイド曲線とは,直線上を円が滑ることなく転がるとき,円周上の1点が描く曲線です(図)。
この問題は,ヨハン・ベルヌーイやライプニッツなどによって解かれ,その答えは直線でも円弧でもなく,サイクロイド曲線と呼ばれる曲線です。(*)1 サイクロイド曲線とは,直線上を円が滑ることなく転がるとき,円周上の1点が描く曲線です(図)。
実際にボールを転がして,昔の数学者たちの努力の結果を確かめて下さい。
このサイクロイドの滑り台には,斜面のどの位置からボールを転がしても最下点に到達するまでの時間が同じである,という性質もあります。(*)2
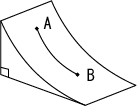 斜面上の2点A,Bを結ぶ曲線に沿って質点が初速0で降下するとき,どんな曲線(測地線のみ考えるからこれは平面曲線)のとき,降下時間が最短となるか。
斜面上の2点A,Bを結ぶ曲線に沿って質点が初速0で降下するとき,どんな曲線(測地線のみ考えるからこれは平面曲線)のとき,降下時間が最短となるか。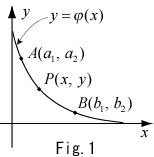 (解)求める曲線を
(解)求める曲線を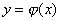 とおく。Fig1において2点
とおく。Fig1において2点 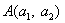 ,
,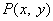 に対し
に対し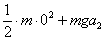 , 点P…
, 点P… 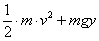 (gは重力加速度)
(gは重力加速度)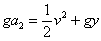
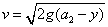 ・・・①
・・・①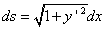 より,速度vは
より,速度vは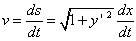
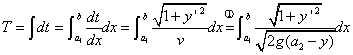
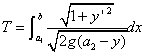 ・・・(1.1)
・・・(1.1)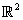 内のc1-class曲線
内のc1-class曲線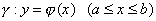 に対し,曲線γの関数
に対し,曲線γの関数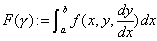 ・・・②
・・・②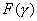 を
を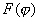 とかく。
とかく。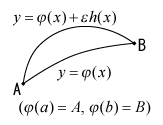 さて,ある関数
さて,ある関数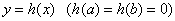 を使って新たな関数
を使って新たな関数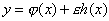 を作る。εを動かすと,これは端点A,Bを固定する曲線族をあらわす。(変分曲線という)
を作る。εを動かすと,これは端点A,Bを固定する曲線族をあらわす。(変分曲線という)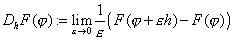 ・・・③
・・・③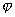 におけるh方向の微分という。②に形で与えられる汎関数
におけるh方向の微分という。②に形で与えられる汎関数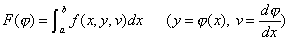
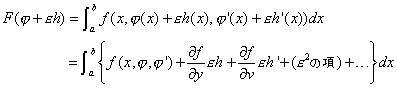
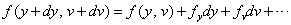 による)
による)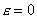 で評価すれば
で評価すれば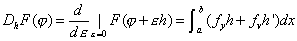
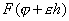 をεの関数
をεの関数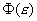 と考えると
と考えると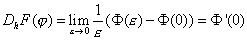 )
)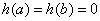 を満たす任意のhに対して
を満たす任意のhに対して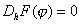
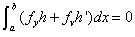 ・・・④
・・・④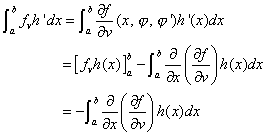
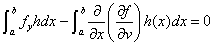
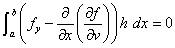
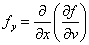 ・・・(注2)
・・・(注2)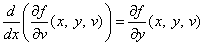 (3・1)
(3・1)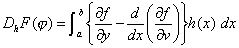
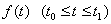 が
が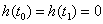 である任意の連続関数h(t)に対して常に
である任意の連続関数h(t)に対して常に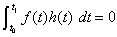 であれば
であれば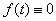 である(証明略)。
である(証明略)。
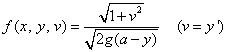 に対し
に対し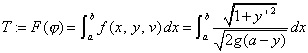
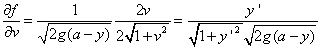
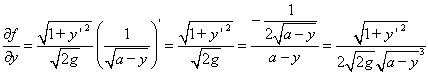
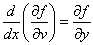 は
は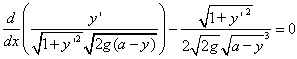

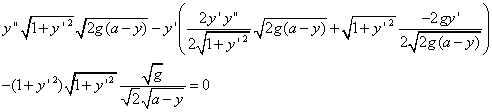
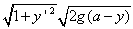 をかけて
をかけて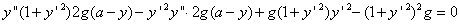
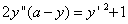
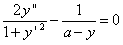
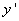 をかけて積分
をかけて積分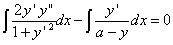 ∴
∴ 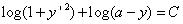
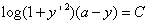 ∴
∴ 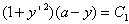
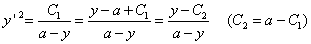
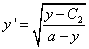 ・・・(5・1)
・・・(5・1)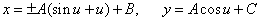
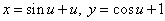 )
)
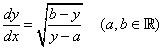 の解法
の解法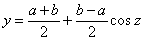 ・・・①とおくと
・・・①とおくと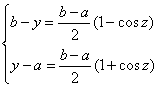 ・・・②
・・・②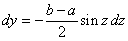 ・・・③
・・・③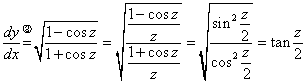 ・・・④
・・・④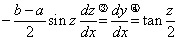
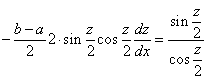
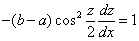
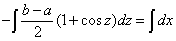
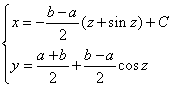
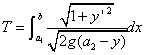 において
において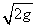 は本質的ではないので,改めて
は本質的ではないので,改めて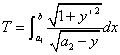 ・・・(6.1)
・・・(6.1)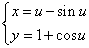 ・・・(6.2)より
・・・(6.2)より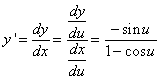
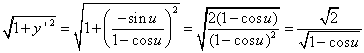
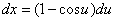 。点Aではa1=0,a2=2だから
。点Aではa1=0,a2=2だから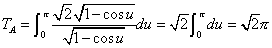 ・・・(6.3)
・・・(6.3)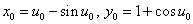
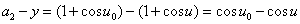
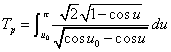 ・・・(7.1)
・・・(7.1)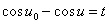 ・・・(7.2)
・・・(7.2)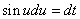
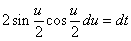
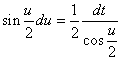
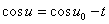
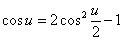
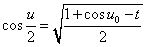 ・・・(7.3)
・・・(7.3)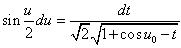
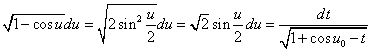 ・・・(7.4)
・・・(7.4)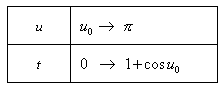
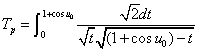 ・・・(7.5)
・・・(7.5)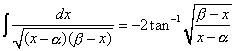 ・・・(8.1)
・・・(8.1)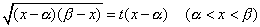
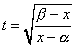 とおくと
とおくと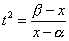 ・・・(8.2)
・・・(8.2)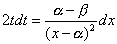
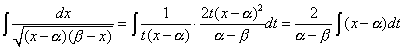
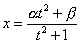 ∴
∴ 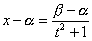
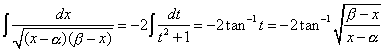
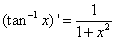 から
から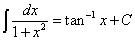 を使った。
を使った。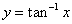 とおくと
とおくと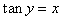 ∴
∴ 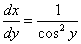
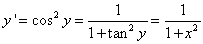 ∴
∴ 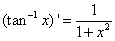
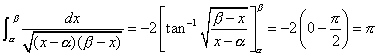
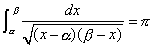 ・・・(8.2)
・・・(8.2)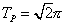 ・・・(9.1)
・・・(9.1)