折り紙と塩山で学ぶ
なわばりの幾何

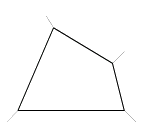 問題 A 問題 A右の図のように4軒の住宅地に囲まれた4角形の公園(空き地)があります。 ある日公園の除雪をすることになり各自の住宅地と公園の境界から最も近い区域の雪かきをすることにしました。 どのように区域割をしたら良いでしょうか。 |
 まず、簡単な場合から考えていきましょう。
まず、簡単な場合から考えていきましょう。 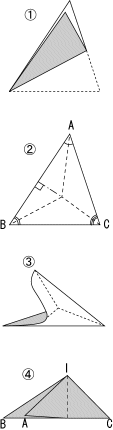
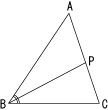
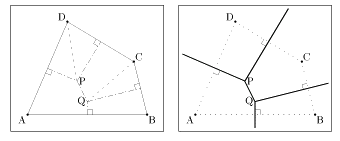
左図において、2辺BA,BCから等距離にある点は∠Bの2等分線上にあります。右図①のように、BAとBCを重ね折ると、この2等分線APを得ることができます。直線APによって辺BA,BCに近い区域が示されました。
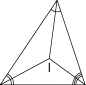 三角形の場合も同様です。三角形ABCの3つの内角の2等分線は1点(内心)で交わり、この線分が区割りを表します。
三角形の場合も同様です。三角形ABCの3つの内角の2等分線は1点(内心)で交わり、この線分が区割りを表します。
折り紙で考えると、3本の2等分線を折り、右図② ~③ のように三角形は内心Iを頂点としてたたむことができます。このとき、3つの辺AB,BC,CA
は一直線上に重なり内心Iから3辺への距離は等しいこと、たたまれた部分が各辺への最も近い区域を表すことが分かります。
塩山でこのことを確かめてみましょう。
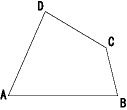
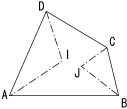 4つの角の二等分線を折ります。一般には4つの2等分線は同時に1点で交わりません。最初に出会った2組の二等分線の交点をそれぞれI,Jとします。この2点I,Jはどんな点なのでしょうか。
4つの角の二等分線を折ります。一般には4つの2等分線は同時に1点で交わりません。最初に出会った2組の二等分線の交点をそれぞれI,Jとします。この2点I,Jはどんな点なのでしょうか。
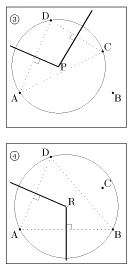
ここで点IからADに垂線IMを折り、ID,IAを折りながらAMとDMが重なるようにたたんでみましょう。すると、Iから新たな折り線ができ、点Jを通ることが分かります。(下図)
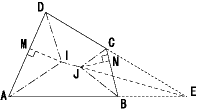
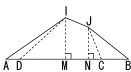 次に、JからもCBに垂線JNをおろし、同様にたたむと、この四角形の4辺は重なり4頂点は1直線に並びます。(左図)
次に、JからもCBに垂線JNをおろし、同様にたたむと、この四角形の4辺は重なり4頂点は1直線に並びます。(左図)
このとき、DC,ABの延長線の交点をEとすると、点Iは△ADEの内心、点Jは△BCEの傍心になっています。これで左図のように四角形の場合の区割りが得られました。すべての区割り線は角の2等分線になっています。塩山でも確かめてみます。
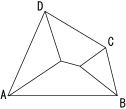 点I,Jは△ADE,△CBEの内心、傍心です。この内心・傍心の選び方は他にも 考えられますが、その場合は内接円(傍接円)が他の辺を横切ることになり最も近いという条件に反します。折り紙はたたむことができません。
点I,Jは△ADE,△CBEの内心、傍心です。この内心・傍心の選び方は他にも 考えられますが、その場合は内接円(傍接円)が他の辺を横切ることになり最も近いという条件に反します。折り紙はたたむことができません。
一般に折り紙の場合、多角形はこのように全ての辺をそろえて折りたたむことができますが、問題Aのような場合は凸多角形の場合に限られます。(凹多角形の場合は一部を放物線に置き換えることが必要です。後述)
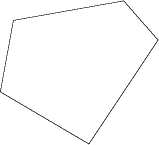 右図のような5角形の場合はどうなるでしょうか。境界線を予想して書き込んでみましょう。 また、折り紙で折ってみましょう。正解は塩山で示してみます。
右図のような5角形の場合はどうなるでしょうか。境界線を予想して書き込んでみましょう。 また、折り紙で折ってみましょう。正解は塩山で示してみます。
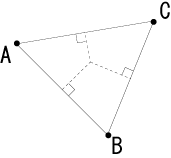
問題 B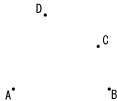 ある地域に4つの高等学校が右の図のようにあります。一人ひとりの生徒はこの4校のうち最も近い学校に全員入学できるとすると校区はどのようになるでしょう。 ある地域に4つの高等学校が右の図のようにあります。一人ひとりの生徒はこの4校のうち最も近い学校に全員入学できるとすると校区はどのようになるでしょう。 |
まず、簡単な場合から考えていきましょう。ここも問題Aと同様に後程塩山で検証してみます。
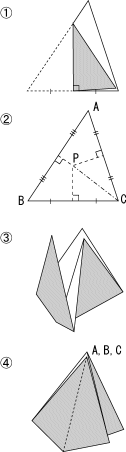 ・学校数が2校のとき
・学校数が2校のとき 学区の境界は線分ABの垂直二等分線(右上図①)
折り紙では2点A,Bを重ねて折ってできる折り線です。
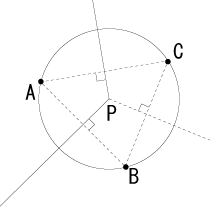
この場合も簡単です。AB,BC,CAの垂直二等分線を引くと、A,B,Cのそれぞれに一番近い区域が示されます。
折り紙では、△ABCにおいて、辺AB,ACの垂直2等分線を折り(谷折り)、交点Pと頂点Cを結ぶ線を山折りにして包むように折ると第3の垂線(辺BCへの)が自然にでき、3頂点A,B,Cは重なります。 (右図、点 Pは△ABCの外心)
| ・折り紙 | ・校区 |
 |
 |
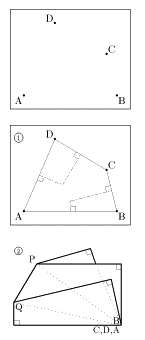
 なぜ2点P,Qなのか。
なぜ2点P,Qなのか。
| 塩山のアイデアは黒田俊郎先生の考案によるものです。2次曲線の話まで及ぶ詳細な内容は冊子「塩が教える幾何学」にまとめられており、インターネットを通じて入手することができます。
(http://users.goo.ne.jp/t-kuroda/) また、「平面幾何のは・な・し」(三省堂:1999.10刊 黒田俊郎著)の中でも一部触れられています。 |
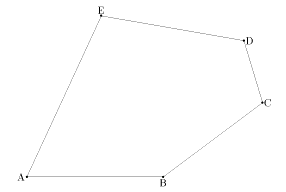 ・課題:学校数が5校のとき
・課題:学校数が5校のとき右図のような5角形の場合はどうなるでしょうか。境界線を予想して書き込んでみましょう。 また、折り紙で折ってみましょう。正解は塩山で示してみます。
 問題 C 問題 Cある地域に商店街Aと総合大型商業施設Bが右の図のようにあります。地域住民が最も近いところで買い物をするとすると、A,Fはどのような領域の住民を客として確保できるでしょうか。 |
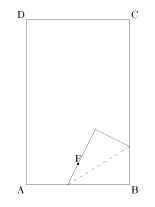 1点と直線からの距離が等しい点の軌跡(放物線)がその境界線となります。
1点と直線からの距離が等しい点の軌跡(放物線)がその境界線となります。
折り紙では、右図のように辺AB上の任意の点が点Fに重なるように折ります。次々と異なる点をFに重ねて折ってできる直線群が一つの曲線(包絡線)=放物線を作り出します。
これによって、問題Aの多角形が凹多角形の場合にも対処できることになります。
これも塩山で見てみることにします。
問題A 1 三角形 2 四角形 3 五角形
問題B 1 三角形 2 四角形 3 五角形
問題C 1 放物線 2 凹5角形 ついでに 2 楕円 3 双曲線










第38回数学教育実践研究会での実演より
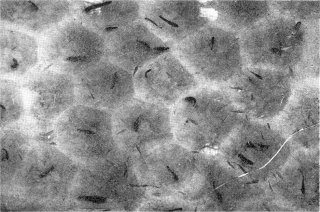
数学セミナー(1995.11)「生物となわばり 杉原厚吉」=魚が砂地に作ったなわばりパターン=より