折り紙と方程式

北海道岩見沢西高等学校
加　藤　渾　一
17-Sep-99

１．折り紙と2次方程式

1.1　等比中項

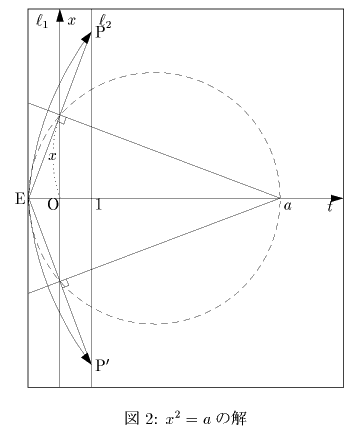
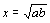　正数a，bの等比中項は，点Qを支点として点Eが直線l2上にくるように折ったとき直線lとの交点として得られます．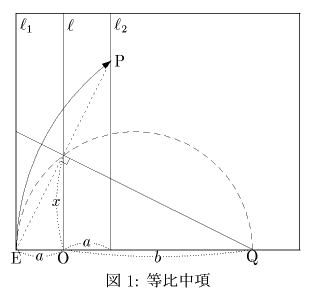
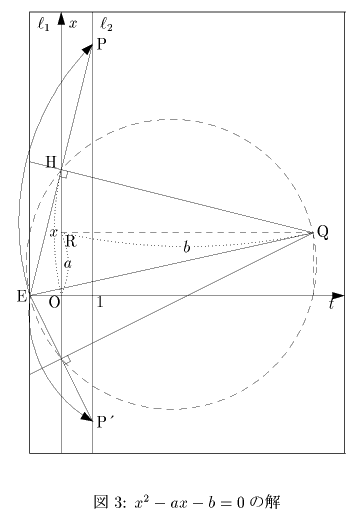
　ただし，EO=a，OQ=b，直線l2は直線lに関して直線l1と線対称とします．

1.2　方程式x2=a（a>0）の解

　EO=1として，上と同様の方法で求めることができます．（図2）
　ただし，点Eをl2にのせる折り方は2通り考えられ，解は2つ存在することが分かります．
　（別紙「平方根を作図する」＝数学玉手箱＝早苗雅史（札幌稲北高校）参照）

1.3　方程式x2-ax-b=0 の解

　図3のように，点Q(b，a)をとりQを支点として点Eが直線l2にのるように折ると線分EP，EP’と直線xとの交点が求める解になります．
　このことは，点H(0，p)とすると，直線HQの方程式は
　　　x=-t/p+p
であり，点Q(b，a)を通ることから
　　　a=-1/p×b+p　　つまり　　p2-ap-b=0
を得る．
　また，この図で△EOH∽△HRQであることからも導くことができます．

　この折り方は，EQを直径とする円と直線xとの交点が解であることを意味しています．
　これはコンパスと定規による2次方程式の解の作図法をも示しています．
　（別紙「2次方程式の解を作図する」＝数学玉手箱＝早苗雅史（札幌稲北高校）参照）

　次に具体的に最近の入試問題を折り紙で解いてみることにします．


２．折り紙的解法の具体例

　長さ1，a，bの線分が与えられているとき，次の問に答えよ．
(1)a2の長さを持つ線分を作図する方法を説明せよ．
(2)√bの長さを持つ線分を作図する方法を説明せよ．
(3)x2-2ax-b=0の正の解の長さを持つ線分を作図する方法を説明せよ．
（97　岩手大学教育学部）

　出回っている解答例はこの3問を個別の方法で誘導的に解いていますが，折り紙の手法を用いると，この3問を以下のように統一的解法で解を得ることができます．

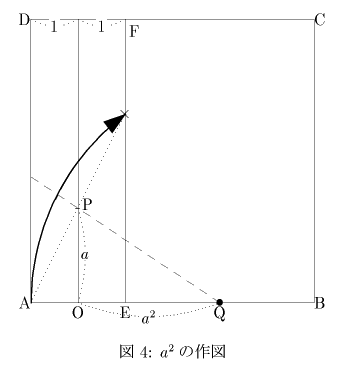
　図4のように，OA=1，OP=aとし，点Pに関して点Aと対称な点をEF上にとるように折ると，OQ=a2が得られる．

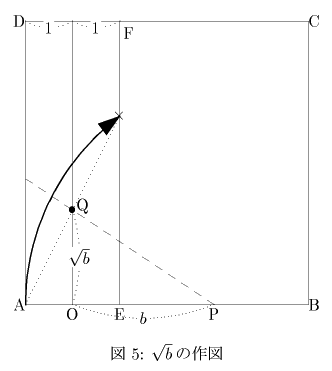
　今度は逆にOA=1，OP=bとし，点Pを支点として点AをEF上にとるように折ると，OQ=√bが得られる．（図5）

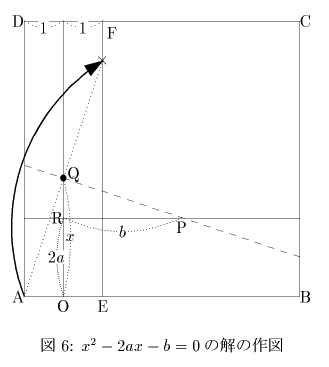
　AO=1，OR=2a，RP=bとし，点Pを支点として点AをEF上にとるように折ると，OQが解である．（図6）


３．折り紙と3次方程式

　折り紙では，コンパスと定規で不可能な，「異なる2点を異なる2直線上に同時に移動する」という折り方が可能です．この事実は3次方程式の折り紙による解法を導きます．
　次図のようにxy平面上に2点E(-1，0)，P(b，a+c)をとります．そして，y軸に関してx=-1と線対称な直線をl2，直線y=aに関してy=a+cと線対称な直線をl1とし，点Eを直線l2上に点Pを直線l1上に同時にのるように折ります．すると2点E，Pと2点E’，P’は折り線 l に関してそれぞれ線対称であり，E’(1，2p)，P’(q，a-c)とします．
　このとき，折り線 l とy軸との交点は(0，p)ですが，このpの値を求めてみましす．

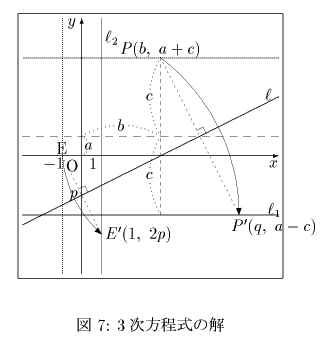
　まず，直線 l の方程式は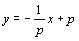です．l はPP’の中点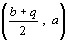を通るから，
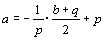　　　　…(1)
　また，l と PP’は垂直であるから，
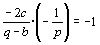　　　　…(2)
(1)と(2)から，qを消去して整理すると，
　　　p3-ap2-bp+c=0　…(3)
を得ます．
　つまり，pは(3)の3次方程式を満たす値です．
　また，(3)の解がすべて実数である場合はこの折り方は一通りではありません．
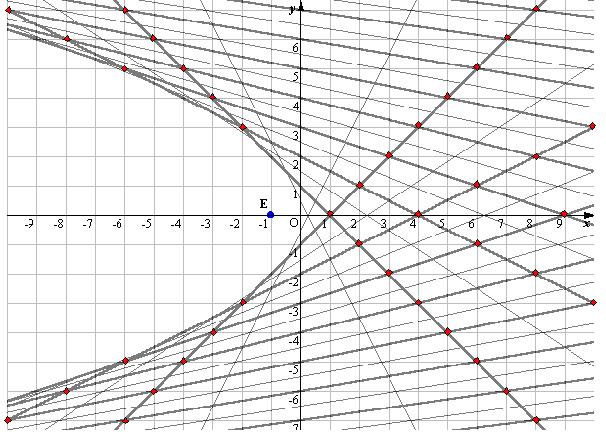
　実際に具体例として，次ページ図10に3次方程式
　　　x3-2x2-5x+6=0
の3つの解を折る折り方を示します．

3次方程式x3-2x2-5x+6=0を解く


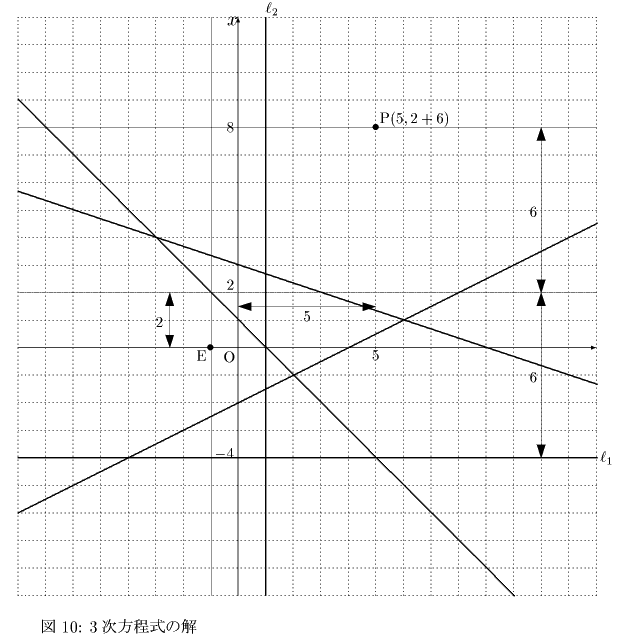
　まず，点P(5，2+6)をとり，点Pと直線x=2に関して対称な点(5，-4)を通り，この直線に対して平行な直線l1を折ります．
　次に点Eを直線l2上に，点Pを直線l1上に同時に移すように折ります．
　すると上図のように斜実線を折り線とする3通りの折り方が考えられます．このとき，これらの折り線とx軸との交点（x=-2，1，3）が解となります．

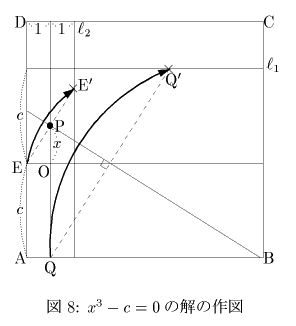
　次に特別な場合として，立方根の作図を考えてみましょう．
　x3=c（c>0）とすると，次の図8のように，点Eをl2上に，点Qをl2上に同時にのせるように折ったとき直線OQ上の点Pが求める解となります．

（補足1）　藤田文章氏は3倍角の公式
　　　
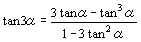
より，α=tan 3α が与えられたとき，t=tan αとして，3次方程式
　　　t3-3αt2-3t+α=0
を解くことによって，角の三等分が可能であることを示しました．（Original Science ＆ Art 1997.8月）
　昨年紹介した阿部氏の方法とは別の解法です．

　この2次方程式，3次方程式の解法は正五角形，正七角形の作図を可能にします．

（補足2）　1次方程式ax=bの解
　下図のように，3点E，Q，Rをとり線分EQを折ります．この線分にOから垂線をおろします．次に点Oがこの垂線上にくるようにRを通る折り線をつくると点Pが求める解となります．

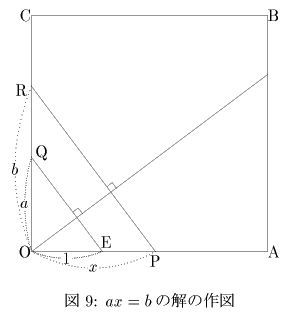
（蛇足）　2次方程式x2-ax-b=0の解発見紙
　a，bのいくつかの値に対応する折り線を同時に引いてみると別紙のような図版を得ることができます．

方程式x2-ax-b=0の解　発見紙