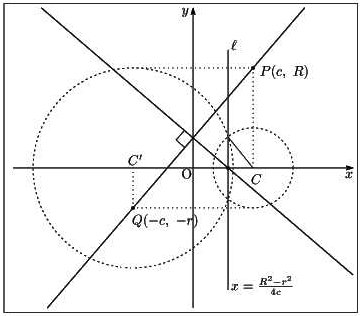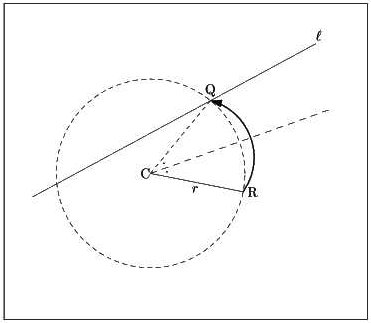
図1:直線と円の交点
そして,(1)と(2)により描かれた直線や円から,
(3) 2直線の交点を求めること.
(4) 直線と円との交点を求めること
(5) 2つの円の交点を求めること
を有限回適用することによって,次々と点や直線や円を描き,条件に適する図形が得られるとき,この図形は定規とコンパスで作図できる,という.
Mascheroniの定理
「定規とコンパスで可能なすべての作図はコンパスだけで求めることができる」
ことを導いている.
この手法を折り紙に適用する.
折り紙による作図では,円を画くことはできないが,(2)に対して,「円は一つの定点から与えられた長さに等しい距離にある任意の点で与えられる」という仮定のもとで
「コンパスと定規で可能な全ての作図は折り紙で求めることができる.」
ことを示すことができる.
(1)と(3)は明らかに可能である.
(4),(5)について可能であることを示す.
(4)について
直線lと定点C,長さrが与えられたとき,点Cから距離rである点をl上に取ることが可能である.(点Cを支点として点Pが直線lに重なるように折る)

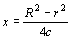 である.この値は次のようにして求めることができる.
である.この値は次のようにして求めることができる.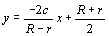 を折ると,x切片が求める値となる.そこで,この点でx軸の垂線lを折り,点Cを支点として距離がrである点を垂線l上にとると,この点が二つの円の交点である.
を折ると,x切片が求める値となる.そこで,この点でx軸の垂線lを折り,点Cを支点として距離がrである点を垂線l上にとると,この点が二つの円の交点である.