複素数 z=a+bi=r(cosθ+isinθ) が z5=1 を満たすとき,次の問いに答えよ.ただし,a,b,rは正の実数で,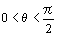 とする. とする.(1) rの値とθの値を求めよ. (2) zを解とする整数係数の4次方程式を求めよ. (3) 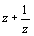 を解とする整数係数の2次方程式を求めよ. を解とする整数係数の2次方程式を求めよ.(4) aの値を求めよ. (新潟大学) |
複素数 z=a+bi=r(cosθ+isinθ) が z5=1 を満たすとき,次の問いに答えよ.ただし,a,b,rは正の実数で,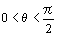 とする. とする.(1) rの値とθの値を求めよ. (2) zを解とする整数係数の4次方程式を求めよ. (3) 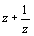 を解とする整数係数の2次方程式を求めよ. を解とする整数係数の2次方程式を求めよ.(4) aの値を求めよ. (新潟大学) |
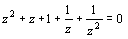
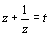 とおくと,求める方程式は (3)t2+t−1=0 である.
とおくと,求める方程式は (3)t2+t−1=0 である.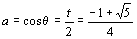
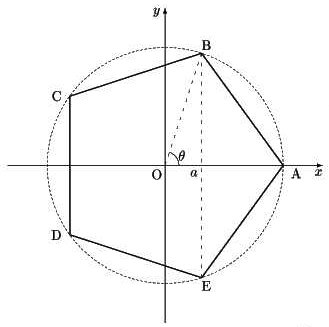
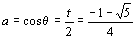 となり,頂点C,Dの位置も定めることができる.
となり,頂点C,Dの位置も定めることができる.
実際の折り紙による作図の場合は,煩雑をさけ t2+t−1=0 の解をそのまま使うために,最初の単位を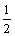 にとる方が分かりやすい.
にとる方が分かりやすい.
次の折り図を参照してください.(折り図は上図を90°回転してある)
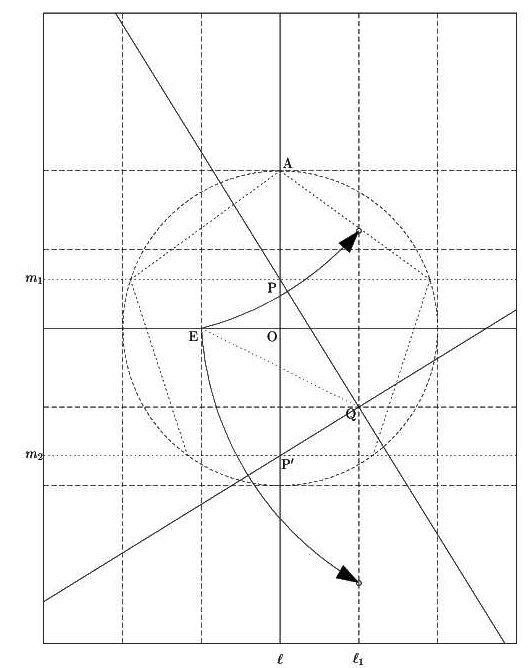
| 奇数辺の多角形が円に内接しかつ内角がすべて等しければ正多角形である. |
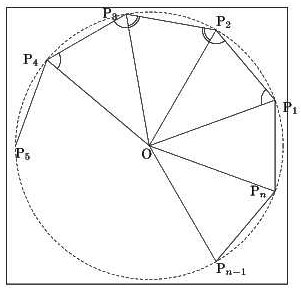 求める辺の長さの辺の垂直二等分線が同一の点を通るように次々と角を合わせていくとよい.
求める辺の長さの辺の垂直二等分線が同一の点を通るように次々と角を合わせていくとよい.
辺数が偶数のときは必ずしもこのことは成立しないのでこの方法は使えない.例えば直角を重ねながら折っていくと長方形になり正方形には必ずしもならない.
[解] 右の図で,∠OP1P2=∠OP2P1,∠OP2P3=∠OP3P2
また,∠P2=∠P3であるから∠OP2P1=∠OP3P4
よって,△OP2P1≡△OP3P4よりP1P2=P3P4
以下同様にして,多角形の辺は一つおきに等しくなる.nは奇数だから
P1P2=P3P4=P5P6=…=PnP1=P2P3=…=Pn-1Pn
となり,すべての辺が等しくなるから正多角形である.
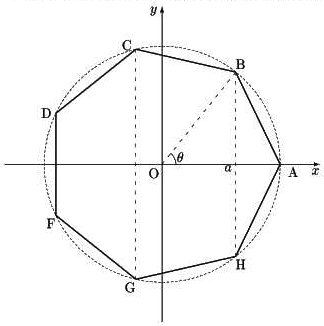
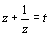 とおいて,t3+t2-2t−1=0
とおいて,t3+t2-2t−1=0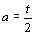 より,正五角形の場合と同様に頂点の位置を定めることができる.
より,正五角形の場合と同様に頂点の位置を定めることができる.