サイクロイド曲線の数学

札幌篠路高校　　真鍋　和弘
（数学教育協議会会員）

1．「転がる」とはどういうことか？

　冬になると北海道では道路が凍結して，スリップによる交通事故が多発し，毎年多くの犠牲者が出ます．冬道で車を運転するときに，タイヤがスリップしている（すべる）のか，スリップしていない(転がる)のかは大変重要なことなのです．「転がる」と「すべる」の違いはわかっているようで，実は結構難しいのです．これを数学できちんと表すためには少々準備が必要です．「転がる」とはどういうことかを理解してもらうために，次の問題を考えてみてください．

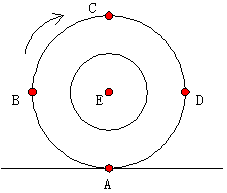
【問題１】

　タイヤが図の方向にスリップしないで転がっているとき，図のA～Eの点の中で，止まっている人から見て瞬間的にとまっている点が1つだけある．それはA～Eのうちどれか？

【答】　Ａ　

　なぜそうなるのか，疑問に思われる方もあるでしょう．このテキストの主題は「転がる」とはどういうことなのかを数学的に表現してみようということなのです．それには3角関数と微分についての知識が必要です．転がるタイヤの円周上の1点が描く曲線はサイクロイドと呼ばれ，よく知られている曲線の1つです．次節でこの曲線の幾何学的性質を調べてみることにします．


2．サイクロイド曲線

　いま半径aの円板がx軸上を図のように回転しながら転がっているとします．円周上の1点Pの座標を(x，y)とし，Pが描く軌跡を考えてみましょう．図のようにPの出発点を原点Oにとり，円板が角θだけ回転して，x軸に点Aで接しているとします．このときのPの位置を求めてみます．円板が完全に転がる条件は，弧APが線分AOにべったりと重なることですから，弧APと線分AOの長さを等しいとおくことができます．

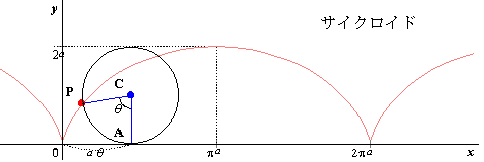
　θを弧度法（ラジアン）で測れば，弧APの長さはaθとなるので，座標(x，y)は
　　　
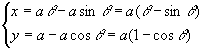
とあらわされることがわかります．－∞＜θ＜＋∞とし，x，yをθの関数と考えると，平面内の集合C
　　　C=｛(x，y)｜x=x(θ)，y=y(θ)，－∞＜θ＜＋∞｝
は曲線を表します．これをサイクロイド（cycloid）と呼んでいます．もしPが円板の内部の点であれば，Pの軌跡は
　　　
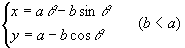
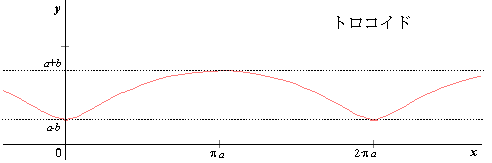
となります．これはトロコイド（trochoid）と呼ばれています．

　一般にこのような表し方を，θをパラメーター（助変数）とする曲線のパラメーター表示といいます．式のかたちからすぐわかるように，サイクロイドやトロコイドはθについて何回でも微分可能な（なめらかな）曲線です．

　さて，θが時間tとともに変化するとすればθはtの関数，θ＝θ(t)と考えられるので，tをパラメータにとることもできます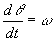．とおき，x，yをtで微分すると
　　　
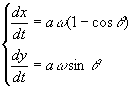
となります．2次元のベクトル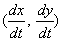はPの瞬間速度を表します．tの関数ω(t)は角速度と呼ばれています（今後，ω＞0とします）．


3．転がるタイヤの運動学

　ここでは，時間tとともに点Pがどのように運動するかを解析してみましょう．歴史的には，このような研究を運動学(kinematics)と呼んでいました．

　まず初期条件として，時刻t＝0で，θ(0)＝0とします．また円板が1回転して，再びPがx軸に接する時の時刻をt＝Tとします．すなわちθ(T)＝2πです．さて時刻t＝Tのときの，点Pの速度はどうなるでしょうか？　前節の式で，θ＝2πとおくと
　　　
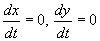
となります．

「転がる」ことの外延（積分）的表現　　　　弧APの長さ=線分AOの長さ
「転がる」ことの内包（微分）的表現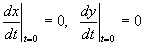　　　　

【定理1】

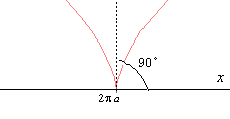
　タイヤ（または円板）が完全に転がっているとき，タイヤの円周上の1点Pはサイクロイド曲線を描いて進み，タイヤが地面に接している点の（地面に対する）速さは0，タイヤの最上部の点の（地面に対する）速さが最大で2aωとなる．


4．ガリレイの相対性原理

　この節では，定理1の直感的な説明を試みることにしましょう．そのためには「ガリレイの相対性原理」と呼ばれる物理学の原理を使うことにします（アインシュタインの相対性原理はガリレイの相対性原理を拡張したものです）．ガリレイの相対性原理とは，「あらゆる力学法則はどのような等直線運動している人から見ても同等に記述される」という原理です．つまり運動を解析するときに，数式ができるだけ簡潔になるような等速直線運動する座標系（観測者）を選んでもかまわないということです．

　そこで，次のような仮定を置くことにします．前節までの議論では，円板の回転はどのような回転（ただし回転の向きだけはθが増大する方向，ω＞0でした）でもよかったのですが，今後，ωは一定とします．でしたから，これを積分して初期条件θ(0)＝0を考慮し，θ(t)＝ωtを得ます．

　次に，運動を記述する座標系を静止系から，円板と同じ速度で移動する座標系に変換します．円板の中心の速度Vは，1回転する時間T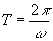（）の間に2πaだけ進むので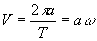，となります．x軸方向に速度V=aωで等速直線運動する座標系から見ると，円板の運動は単なる回転運動だけとなり，解析が非常にらくになるのです．

　このことを具体的に示してみます．新しい座標系からみた点Pの座標を(x'，y')とすると，もとの座標系(x，y)との関係は，
　　　
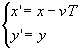
で与えられます．力学ではこれをガリレイ変換と呼ばれています．これをx，yについて解き，サイクロイドの表式に代入すると，
　　　
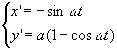
となります．ここで，関係式θ＝ωt，V＝aωを使いました．(x'，y')の軌跡は，図のように中心(0，a)，半径aの円を表すことがわかります．つまり，新しい座標系から見ると，Pは回転運動だけをすることが確かめられました．

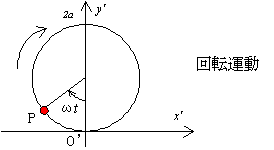
　このことは，次のことを意味しています．「タイヤといっしょに運動している人から見ると，タイヤは回転運動だけしているように見える」　これは，自動車に乗っている人は常に感じていることです．その代わりに，地面が速さVで進行方向と反対の方向へ動いているのが見えるはずです．

　このようにサイクロイド運動は直線運動＋回転運動という合成によって作ることができます．定理1で，タイヤが地面に接した瞬間，タイヤの接点の速度（地面に対する）は0になることがわかりました．これはタイヤといっしょに運動している人から見ると，タイヤの円周上の点Pが地面に接する瞬間の回転速度aω（進行方向と逆向き）と，地面の運動の速度V（進行方向と逆向き）が一致していることから必然的に導かれる結論です．


5．ガリレイのパラドックス

　イタリアの有名な科学者ガリレイは次のようなパラドックスを考えました．前と同様に半径aの円板がx軸上を回転しながら転がっているとします．内側に半径bの同心円を考えると（b＜a），半径aの大きな円板の運動に連動して，半径bの小さな円板も回転しながら進むことになります．

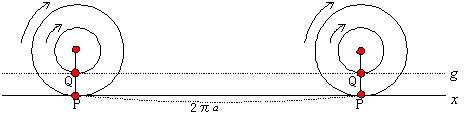
　上図のようにx軸上に平行な直線gを考え，これに小さな円板が接しながら回転しているとします．大きな円板とx軸との接点をPとし，円板の中心とPを結ぶ線分が直線gと交わる点をQとします．円板が回転している時，大きな円板の円周上の点Pに対し，小さな円板の円周上の点Qが必ず1：1に対応しています．また円板が1回転するとき，大きな円板の円周上の各点とx軸上の各点，および小さな円板の円周上の各点と直線g上の各点とが1：1に対応しています．この時次のようなパラドックスが生じます．

　大きな円板が1回転するときと，円周に等しい距離（2πa）を進みます．同じ時間に小さな円板も1回転し，やはり等しい距離（2πa）を進みます．しかも小さな円板は常に直線gにくっついて回転しているので，途中でとんだり，すべってはいないように思えます．これでは円板の半径に関係なく，1回転して進む距離はみな等しくなってしまいます．言い換えれば，同心円の円周の長さはすべて等しくなってしまいます．どこが間違っているのでしょうか．

　ガリレイは晩年の自著「新科学対話」のなかで，このパラドックスが生じる理由をうまく説明しています．しかし，今までの知識を使えば，このパラドックスを完全に解くことができます．

【パラドックスの正解】

　実は，小さな円板は直線g上をすべっているのです．なぜなら，円板の中心と同じ速度aωで走っている人から見ると，小さな円板の円周上の点Qの速度は，x軸と反対方向へbωです（直線gとの接点において）．このとき直線gはx軸と反対方向へ速度aωで進んでいるので，速度差(a－b)ωが生じます(b＜a)．速度差があるということは，すべっているということです．

　今度は止まっている人からこの現象を見てみることにしましょう．今度は小さな円板の円周上の点Qの軌跡は§2のトロコイド
　　　
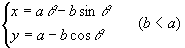
を描きます．上の式を時間tで微分すると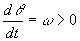（とします）．
　　　
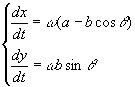
となるので，Qの速さvは
　　　
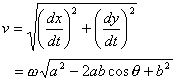
で与えられます．

　簡単な計算でa≠bなら，v≠0となることが証明できます．つまり小さな円板の円周上の点Qは決して止まることがないのです．言い換えると，やはり小さな円板は常に直線gを「すべりながら」転がっていることがわかります．

【演習問題】

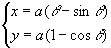  1. §2のサイクロイド曲線の式　　を導け．

    同じく，トロコイドの式　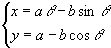　を導け．

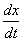  2. §2で，点Pの速度のx成分をθの関数としてグラフを描け．

    同様に，y成分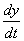をθの関数としてグラフを描け．

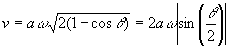  3. §3で，点Pの速さ　　を導け．

    また，vをθの関数としてグラフを描け．

  4. §5で，点Qの速さvが決して0にならないことを示せ（ω＞0，b＜aとせよ）．

  5. サイクロイド曲線がx軸となす角が90°となることを示せ．


【参考図書】