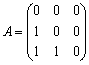�k�@���@��
��S�Q�� ���w������H������
�|���猻��̂������b�����|
�s��ɂ��������q�̍\��
����1�S�N�W��3��(�y)
�k�C�����M���z�����w�Z
�k�C���Ύ�썂���w�Z
���w�ȋ��@ ���I ����
�P�A�͂��߂�
�@�s��ɂ��������q�Ƃ́C�Ⴆ��
�@�@�@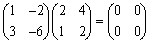 �@�@
�@�@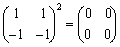
�̂悤�ɁC�`���n�C�a���n�C�`�a���n �����藧�Ƃ��C�`�C�a�����q�Ƃ����B
�i���́w����q�x�̒�`�́C��q�̒ʂ萔�w�I�Ȓ�`�Ƃ��Ă͞B����������̂ŁCDef�W�ʼn��߂Ē�`���邱�ƂɂȂ�B�j
�@�{�e�̖ړI�́C�w�s��ɂ��������q�Ƃ͂����Ȃ�\�������Ă��邩�x�Ƃ������k����̎���ɉ����邱�ƂƁC���^�㐔�w�ɂ�����w����q�����x�ł���B
(1)�@���Z���ɂƂ��Ă̗���q
�@���Z���ɂƂ��ď��߂Ă̗���q�Ƃ̏o��́C�V�N�ȋ����ł���B�{�Z�ł��C���Đ��w�b�̎��ƂŐ��k����w�s��ɂ��������q�Ƃ͂����Ȃ�\�������Ă��邩�x�w�ǂ�����Η���q�������̂��x�Ƃ������₪����������łȂ��C��N�̖{�Z���k�̉���J�p���N�́C�ȉ��̒ʂ�̏����������݂��B
(2)�@���k�̏������i�v�|�j
�@�`���̂悤�ȗႩ��C2���̐����s��ɂ��āw����q�ˋt�s��������Ȃ��x���Ƃ��\�z�����̂ŁC�����w���@�ɂ���ďؖ��B�i�K�v�����j
�@�Ƃ��낪�C�t��
�@�@�@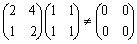
�̂悤�ɁC�w�t�s��������Ȃ��x����Ƃ����āw����q�x�ɂȂ�Ƃ͌���Ȃ��̂ŁC�\�������ɂ��Ă��l�����B�i���̂Ƃ��C���̕��ł́C�s�x�N�g�����C��x�N�g����'�����̎�����^�����B�j
�@�@�@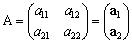 �@�@
�@�@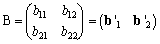
�Ƃ����Ƃ��C�K�v�������C��1//��2�C��'1//��'2�ł��邪�C�K�v�\�������Ƃ���
�@�@�@�w�`�a���n����i�E��'j���O�@�́@��i����j�@�@1����i�C����2�x�@�@��
�����B
�@���āC���N�́C����2���̏ꍇ��3���ɒP���Ɋg�������B�܂�
�@�@�@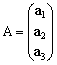 �@�@
�@�@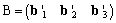
�Ƃ����Ƃ��C�K�v�������
�@�@�@��i//��j�C��'i//��'j�@�@�@1����i�Cj��3
�ƁC�����_���Ă��܂����B���ʁi2�����j�Ƌ�ԁi3�����j�Ƃ̃M���b�v�ł���B
(3)�@���Z�������ɒ��ϓI�Ȑ���
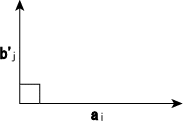 �@�����s��`�C�a��2���܂���3���̂�����ɂ��Ă��C�w����q�x�ɂ��ẮC�����������Ă��邪�C���ꂾ���ł͎c�O�Ȃ���\���I�ɂǂ��Ȃ��Ă���̂��킩��Ȃ��B
�@�����s��`�C�a��2���܂���3���̂�����ɂ��Ă��C�w����q�x�ɂ��ẮC�����������Ă��邪�C���ꂾ���ł͎c�O�Ȃ���\���I�ɂǂ��Ȃ��Ă���̂��킩��Ȃ��B
�`�C�a��2���̂Ƃ�
�@���k�̉̂Ƃ���ł���B
�@�@�@��i����'j�@�@�@�i1����i�Cj��2�j
�@�i������C�e��i���m�C�e��'j���m�����s�j
�@�@�@1����i�Cj��2
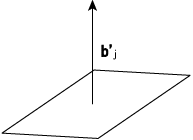 �`�C�a��3���̂Ƃ�
�`�C�a��3���̂Ƃ�
�b�`�r�d1�F
�`�C�a��2���̂Ƃ��̒P���Ȋg���B���̂Ƃ��C��i�C��'j��1�̕��ʃ����肵�Ă���B
�i��3������Ԃ��^��������Ƃ����B�j
�b�`�r�d2�F
��i��1�̕��ʃ����肵�āC����'j
�i���̂Ƃ��C���o��'j�p�̒�����ԁC�܂��́o��'j�p���̒�����ԂƂ����B�j
�b�`�r�d3�F
��Ƌt����'j��1�̕��ʃ����肵�āC����i�i������Ԃ����l�j
�܂Ƃ߂�ƁC��ԁi3�����j�ł�
�@�@�w������������i���܂ޕ��ʃ܂��͒������ƁC��'j���܂ޕ��ʃ��܂��͒��������C�����x
�@(���̂Ƃ��C���ʃC�������ʃ��C�������̒�����ԂƂ����)
�@��ʂɁC������������Ɋg������ƁC��������Ԃ𐂒���2�̕�����Ԃv1�C�v2�ɕ��������Ƃ��C���̂v1������i���C�v2������'j���Ƃ�C������������B
�@�ȏ�̂悤�Ȓ��ϓI�Ȑ����ł́C�������Ɍ�����B���Z�̐��w�b�͈̔͂ł͐��m�Ș_�͂ł��Ȃ��킯�ł���B�����ŁC�e�[�}�������܂ł�����q�Ɍ����āC���^�㐔�w�̗̈�Ɉꕔ���ݍ��B����ɂ���āC4�����ȏ�̒��ۓI�ȃx�N�g��������K�v�������R�ɔ[���ł���͂��ł���B�����ɁC���^�㐔�w�̓��@�Â��ɂ����蓾����̂ƍl����B
�Q�D����q�̍\��
�`�C�a�C�b�͂n�i��s��j�łȂ��Ƃ���B�܂��C����2�̃e�[�}�ɂ��čl����B
�T�@�`�a���n�ƂȂ�`�C�a�̕K�v�\�������͉����H
�U�@�C�ӂ̍s��`��^�����Ƃ��C�`�a���n�C�b�`���n�ƂȂ�a�C�b�����ꂼ��\������B
|
�@�ȉ��C���^�㐔�w�̒��ŁC�K�v�Ƃ����`�iDef�j�C�藝�iTh�j�C����iPro�j�̂݊m�F���Ă����B�藝�iTh�j�C����iPro�j�̏ؖ��́C���ׂĕW���I�Ȑ��^�㐔�w�̃e�L�X�g�C�Ⴆ������Y���w���^�㐔�w�x�i�����o�ł���Ă��钆�ōł��Q�l�ɂ����Ē������j�����Q�ƒ��������B�Ȃ��C�{�e�ɒ��ڊW���閽��iPro�j�ɂ��ẮC�ł��邾���ؖ���t�����B
(1)�@��{�p��C�L��
�@�x�N�g����ԁi�܂��͐��^��ԁj�Ƃ́C�x�N�g�����Z����`�ł���W���������B�����ŁC�x�N�g�����Z�Ƃ́C�u���x�N�g���̏W���C�j���q�i�����̏W���j�Ƃ���Ƃ�
�@�@�@�@ �u�����C�������{�����u�@�@�@�A �u�����C�j�����˂������u
���̂Ƃ��C�u���x�N�g����ԂƂ����B
(2)�@�������x�N�g����Ԃɂ���
�@�x�N�g���̐����́C���ׂĎ����Ƃ���B
�@��=�ia1�Ca2�j��2�����x�N�g���C��=�ia1�Ca2�Ca3�j��3�����x�N�g���C������g�����āC��ʂ���=�ia1�Ca2�C�c�Can�j��n�����x�N�g���Ƃ����C�un�ŕ\���B
�@n�����x�N�g����Ԃł́C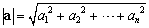 �����̐�Βl�C�����=a1b1�{a2b2�{�c�{anbn���������̓��ςƒ�`����ƁC
�����̐�Βl�C�����=a1b1�{a2b2�{�c�{anbn���������̓��ςƒ�`����ƁC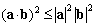 ���
���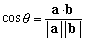 �Ȃ�Ƃ���`�ł���̂ŁC������������̂Ȃ��p�Ƃ����B������������O�̂Ƃ��C���Ƃ��͐����Ƃ������ۂ��ŕ\���B
�Ȃ�Ƃ���`�ł���̂ŁC������������̂Ȃ��p�Ƃ����B������������O�̂Ƃ��C���Ƃ��͐����Ƃ������ۂ��ŕ\���B
Def1�i������ԁj
�u���v�ɂ��āC�v���u�Ɠ����x�N�g�����Z����`�ł���W���̂Ƃ��C�v���u�̕������(Sub Sp.)�Ƃ����B�܂�C�v���u�̕������(Sub Sp.)�Ƃ́C�u���v����
�@�@�@ �v�����C�������{�����v�@�@�A �v�����C�j�����˂������v
Def2�i������ԁj�|���ꂪ����q�̃L�[���[�h�ƂȂ�
�u���v�FSub Sp.�ɑ��āC�v���߁o�����u�F��������O�C�������v�p�Ƃ����Ƃ��C���̂v�����C�u��Sub Sp.�ƂȂ邪�C�������ɂv�̒�����ԂƂ����B
Def3�i�ϋ�ԁC�a��ԁj
�u���v1�C�v2�FSub Sp.�Ƃ���Ƃ��C
�@�@�@�v1���v2�߁o���F�����v1�C�����v2�p
�@�@�@�v1�{�v2�߁o��1�{��2�F��1���v1�C��2���v2�p
���C�u��Sub Sp.�ƂȂ邪�C���ꂼ��v1�C�v2�̐ϋ�ԁC�a��ԂƂ����B
Def�S�i1���Ɨ��C1���]���j
�u���v�FSub Sp.�Ƃ���B�v����i�C�j����i�@1��i��r�ɑ��āC
(1)��1��1�{�c�{��r��r���O�@�ˁ@��1���c����r���O�̂Ƃ��C�o��1�C�c�C��r�p���C1���Ɨ��iindep�j
(2) (1)�̔ے�C�܂�C�j����i��O�i1��i��r�j s.t.�@��1��1�{�c�{��r��r���O����������Ƃ��C�o��1�C�c�C��r�p���C1���]���idep�j�Ƃ����B
Def�T�i�����j
�u���v�FSub Sp.�Ƃ���B�v����i�C1��i��r�ɑ��āC�o��1�C�c�C��r�p��indep�C���C�v�������ɑ��āo��1�C�c�C��r�C���p��dep�̂Ƃ��C�����v�̎����C�o��1�C�c�C��r�p���v�̒�ibase�j�Ƃ����Cdim�v�����C�v���o��1�C�c�C��r�p�ƕ\���B
Def�U�i1���ʑ��j
�u�C�u'�F�x�N�g����Ԃɑ��āC���F�u�˂u'��1���ʑ��Ƃ́C�j�����C���C�u�������C���ɑ��āC��(�����{����)������(��)�{����(��)
Def�V�i1���ʑ��̑��Ɗj�j
�u�C�u'�F�x�N�g����Ԃɑ��āC���F�u�˂u'��1���ʑ��̂Ƃ���(�u)�߁o��(��)���u'�F�����u�p���u�̂��ɂ�鑜�Ƃ����CIm���ŕ\���B
��'(�O)�߁o�����u�F��(��)���O���u'�p���u�̂����j�Ƃ����CKer���ŕ\���B
Remark�@�u'��Im���Csub.�����D�C�u��Ker���Csub.�����D�ł���B
Th1�i1���ʑ��ƍs��j
�un�C�um�F�x�N�g����ԁ@�ˁ@���F�un�˂um��1���ʑ��@s�Dt�D��(��)���`���@�������un
�@���́i���C���j�s��`�́C���ɂ���Ĉ�ӓI�iunique�j
Remark�@1���ʑ����ƍs��`����Έ�Ή�����̂ŁC���Ƃ`�ꎋ�����
�@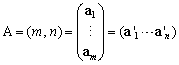 �Ƃ����Ƃ��C
�Ƃ����Ƃ��C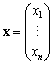 �ɑ���
�ɑ���
�@�@Im����Im�`���o�`���F�����un�p���o��'1 �c ��'n�p�CKer����Ker�`���o�����un�F�`�����O�p
�@�um��Im�`�Csub.�����D�C�un��Ker�`�Csub.�����D�ł���B
Th2�i1���ʑ��Ǝ����j
���F�un�˂um��1���ʑ��C��(��)���`�� �������un
�@�@�ˁ@dim��(�un)�����|dim(Ker��)�C�܂�dim(Im�`)�����|dim(Ker�`)
Remark�@1���ʑ����ɂ���āC��������dim(Ker��)����̂ŁCdim(Ker��)��މ������Ƃ����
Cor�@���F�un�@�ˁ@�um��1���ʑ��C�un���vs�Fsub.�����D
�@�ˁ@dim��(�vs)�����|dim(Ker�����vs)
Prop1�i������ԂƎ����j
�u���v�Fsub.�����D�Ƃ��āC�u���v�{�v���C�v���v�����ӂ����藧�Ƃ���B
���̂Ƃ��C�u���v�Ƃv�ۂ̒��a�Ƃ����C�Ȍ�u���v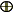 �v���ŕ\���B
�v���ŕ\���B
Cor�@�un��Ker�`���o�����un�F�`�����O�p�ɂ��āC�un��Ker�`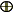 (Ker�`)��
(Ker�`)��
Remark�@�����ŁCKer�`��{��1 �c ��m}���C(Ker�`)����{��1 �c ��m }�Ƃ���C���������B
Th3�i�s��̊K��rank�j
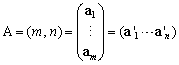 �@�ˁ@dim{��1 �c ��m }��dim{��'1�c ��'n}��dim Im�`
�@�ˁ@dim{��1 �c ��m }��dim{��'1�c ��'n}��dim Im�`
�@���̌��ʒ�`����鎟�����C�s��`�̊K���Ƃ����Crank�`�ŕ\���B
Cor�@rank�`��dim(I���`)�����|dim(Ker�`)
�i�ȏ�C���^�㐔�w�̏����j
(3)�@�T �`�a���n�ƂȂ�`�C�a�̕K�v�\�������͉����H
�`���i���C���j�C�a���i���C���j�Ƃ���B
Prop2�@�`�a���n�@�́@Im �a��Ker �`
pr) �����w�`�a���n����i�E��'j���O�@�́@��i����'j�x�y��Prop1��Cor��萬���B ��
Prop2�́C�T�̉Ƃ��Ė����ł��邪�C����ɂ��ĕ⑫����B
Cor�@�`�a���n�@�ˁ@rank�`�{rank�a����
pr) Prop2�ɂ��C�`�a���n�@�ˁ@Im�a��Ker�`�@�ˁ@dim(Im �a)��dim(Ker�`)
�@�@�@�@�@�@�@�@�@�@�@�@�@��dim(�h���a)�����|rank�`�m��Th3��Cor�n
�@�@�@�@�@�@�@�@�@�@�@�@�@��rank�a�����|rank�`�@��
�@��L��Cor�́C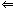 �����藧�Ƃ͌���Ȃ��B�����ŁC����q�����߂Ē�`����B
�����藧�Ƃ͌���Ȃ��B�����ŁC����q�����߂Ē�`����B
Def�W�i����q�̒�`�j
�`������q�Ƃ́C�n�łȂ��`�ɑ��� �a���n ���D���D�`�a���n �܂��� �a�`���n
�@���̂悤�ɒ�`���āC�wrank�`�{rank�a�����x�����肷��ƁC�`�ɑ��āwIm�a��Ker�`�x�܂�a���i��'1�c��'l�j��Ker�`��{��1�c��m}����sub.sp.�ƂƂ�CCor�� �������B
���̌��ʁC�T�̉Ƃ��āw�`�a���n�@�́@rank�`�{rank�a�����x��������B ����
Remark�@�����́C��s����܂ށB1��rank(�`,�a)�����|1�̂Ƃ��C����q�ł���B
(4)�@�U�@�C�ӂ̍s��`�ɑ��āC�`�a���n�C�b�`���n�ƂȂ�a�C�b�����ꂼ��\������B
�@�`�a���n�ƂȂ�a�̍\���ɂ��ẮC3�Ŗ��炩�ɂȂ����B
���ɁC�b�`���n�ƂȂ�b�̍\���ɂ��ẮC�b���i���C���j�s��Ƃ���Ɓ������C�w�b�`���n�@�́@rank�b�{rank�`�����x��������B
��̓I�ɂ́CProp1���g���ƁC�um��Im�`�Fsub.sp.���C�um��(Im�`)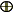 (Im�`)l
(Im�`)l
(Im�`)���߁o�����um�F�����'i���O�C1���͂������p
�@�@�@�@���ot�����um�Ft���`���O�p
�@�����ŁC�s�x�N�g���Ft�����i��1�c��m�j���um�͂um��sub.sp.�ł���B����āC
�@�@�@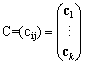 �@��i���um�@1���͂�����
�@��i���um�@1���͂�����
�̍\���́C�`�ɑ��āC�o��1�c��k�p��(Im�`)����sub.sp.�ƂƂ�悢�B
Prop3�i�U�̉��p��Ƃ��āC�k�C����w���w�����ȑ�w�@���i������肩��j
�`�C�a�F�n�łȂ��������f�����s��Crank�`�{rank�a����
�@�ˁw���n�@s.t.�@�`�w���w�`���n�@���@�a�w���w�a���n
�R�D����q��Caylay-Hamilton�̕�����
�@�����s��Ɍ���ƁC����q�̑��݂Ƃ��̍\���́CCaylay-Hamilton�̕�����(�ȉ��C�b�g�d�Ɨ���)���疾���ł���B�ȉ��C�`���i��ij�j�F���������s��Ƃ���B
�@�܂��C�w�`������q��det�`���O�x�͔w���@�ɂ���Đ����B���̋t���������邱�Ƃ��C�b�g�d����ؖ�����Ƌ��ɁC�`�ɑ���Def�W�̂a����̓I�ɂ͍\������B�ŗL�l�ɂ��Ă͊��m�Ƃ��C�`�̌ŗL����������A(��)���O�C�b�g�d����A(�`)���n�Ƃ���B
(1)�@2���̐����s��̂Ƃ�
�@���Z�̐��w�b�͈̔͂ł���B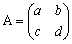 �Ƃ����ƁC�b�g�d�́Cdet�`���O���
�Ƃ����ƁC�b�g�d�́Cdet�`���O���
�@�@�@��A(�`)���`2�|�i���{���j�`���n�@�ˁ@{�`�|(���{��)�d}�`���`{�`�|(���{��)�d}���n
����āC�`���n�ɑ��āC
�@�@�@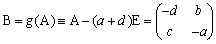
�Ƃ����C�a���n�C�a�`���`�a���n ����āC�`�͗���q
(2)�@�����̐����s��Ƃ�
�@�܂��C�ŏ��������ɂ��ď�������B�ȉ��C�������͂��ׂăX�J���[�W���Ƃ���B
Def�X�i�ŏ��������j
��(�`)���n�ƂȂ�`�̑�������(�`)�̒��ŁC�`�̎������ŏ����`�̍ō����̌W����1�̂��̂��`�̍ŏ��������Ƃ����C��A(�`)�ŕ\���B��A(�`)���n�ł���B
Prop�S�@��(�`)���n�ƂȂ�C�ӂ̑�������(�`)�ɑ��āC��(��)�̓�A(��)�Ŋ�����B
Cor1�@�`�̌ŗL��������A(��)�́C��A(��)�Ŋ�����B
Cor2�@��A(��)���O�@�ˁ@��A(��)���O
�i�ȏ�ŏ��������̏����j
Prop�T �`������q��det�`���O
pr�j�˂͐������Ă���̂ŁC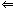 �ɂ��Ď����B
�ɂ��Ď����B
�@�b�g�d�́Cdet�`���O���
�@��A(�`)���`n�{��1�`n-1�{�c�{��n-1�`���n
�@�@�ˁ@�`�o�`n-1�{��1�`n-2�{�c�{��n-1�d�p���`�o�`n-1�{��1�`n-2�{�c�{��n-1�d�p���n
����āC�`���n�ɑ��āC��1(�`)�߂`n-1�{��1�`n-2�{�c�{��n-1�d�Ƃ����C
��1(�`)���n�̂Ƃ��C�`��1(�`)����1(�`)�`���n���C�`�͗���q�C���̂Ƃ��a����1(�`)
��1(�`)���n�̂Ƃ��C��A(��)�����i��n-1�{��1��n-2�{�c�{��n-1�j��肆A(�O)���O
Prop3��Cor2��胳A(�n)���n�C����āCProp3��肇1(�n)���n ����n-1���n
���ɁC��1(�`)���n�ɂ��āC��A(�`)���n�Ɠ��l�Ȃ��Ƃ��J��Ԃ��ΗL�����
�@�@�@�`(�`�{��1�d)��(�`�{��1�d)�`���n
��B�����ŁC��n-1(�`)�߂`�{��1�d�Ƃ����ƁC
�@�@�@��n-1(�`)���n�̂Ƃ��C�`��n-1(�`)����n-1(�`)�`���n���C�`�͗���q�C�a����n-1(�`)
�@�@�@��n-1(�`)���n�̂Ƃ��C��1���O�C���̂Ƃ��C��1���c����n-1���O���`n���n
����āC�`�͗���q�C���̂Ƃ��a���`n-1�@�@�@��
�S�D�p��s��
Def10�i�p��s��j
�`�F���������s��Ƃ���B�`m���n ���� �`m-1���n�ƂȂ�`�����p��s��Ƃ����B
�@�p��s��́CDef�X�������q�̓��ʂȏꍇ�ł���B���̙p��s��̍\���ɂ��čl����B
Prop�U�@�`���i���C���j�C�a���i���C���j�Ƃ���Brank�`�{rank�a�|����rank�`�a
pr) �a��(��'1�c��'l)�Ƃ����ƁC
�@�@rank(�`�a)��dimIm(�`�a)��dimIm�`(��'1�c��'l)�@�m��Th3�n
�@�@�@�@�@�@�@�@�@�@�@�@��dim(��'1�c��'l)�|dim(Ker�`��{��'1�c��'l})�@�m��Th2��Cor�n
�@�@�@�@�@�@�@�@�@�@�@�@��dim(��'1�c��'l)�|dim(Ker�`)
�@�@�@�@�@�@�@�@�@�@�@�@��rank�a�|(���|rank�`)�@�m��Th3�y��Cor�n
�@�@�@�@�@�@�@�@�@�@�@�@��rank�`�{rank�a�|���@�@�@��
Prop�V�@�`1�C�`2�C�c�C�`m�F���������s��Ƃ���B
�@�@�@rank�`1�{rank�`2�{�c�{rank�`m�|(���|1)�� ��rank�i�`1�`2�c�`m�j
pr) Prop�U���J��Ԃ��g���B�@�@��
Cor �`�F���������s��Ƃ���B�`�F���p��s���rank�`��(���|1)���^��
pr) Prop�V�ŁC�`1���`2���c���`m���`�Ƃ����@�@��
Prop�W�i�p��s��ƌŗL�l�j
�`�����p��s��C�܂�`m���n ���� �`m-1���n�̂`�̌ŗL�l�͂��ׂĂO
pr) �i�ˁj�`�̔C�ӂ̌ŗL�l���ɂƂ���ƁC�������O�@���D���D�`��������
����āC�`m�����`m-1�i�`���j���`m-1�i�����j���Ɂi�`m-1���j
�ȉ����l�ɂ��āC�`m������m���������B�@�`m���n����m���O ���Ɂ��O
�i �j�`�̌ŗL��������A(��)���O�̂��̉���1�c��n�ɂ��āC
�j�`�̌ŗL��������A(��)���O�̂��̉���1�c��n�ɂ��āC
��1���c����n���O�@����āC�ɂ̂�����������A(��)���O�̉��ƌW���̊W���C
�e�W����k���O�i����1�C2�C�c�C���j�@�@���`n���n
����āC�������@���D���D�`m���n ���� �`m-1���n�@�@�@��
Cor1�@�`�����p��s��@�ˁ@�b�g�d��A(�`)���n�ɂ�����e�W����k���O(����1,2�C�c�C��)
Cor2 �`�����p��s��@�ˁ@������
Remark ����Cor2�̌��ʁC���p��s��`�̍\���́C�������Ȃ邍�ɂ��Ē��ׂ�悢�B
�@���_���Cor1�ɂ�邪�CProp�V��Cor���L�͂Ȏ�|����ƂȂ�B
Prop�X�i2���̙p�s��j
�@�@�`2���n�C�`���n�@�́@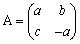 �@�@�������C��2�{�������O
�@�@�������C��2�{�������O
pr�j 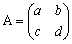 �Ƃ����ƁC�b�g�d��det�`���O�y�т`2���n���C(���{��)�`���n
�Ƃ����ƁC�b�g�d��det�`���O�y�т`2���n���C(���{��)�`���n
�@�@�@�����{�����O�@�@�����|���@����āC�����B�@�@�@��
Cor �i�`�|�ɂd�jk���n�C�͂���2�@�ˁ@�`���ɂd �܂��� �ɂd�{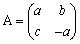
Prop10�i3���̙p�s��j
�@�@�`2���n�C�`���n
�@�@�́@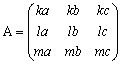
�@���C�����i�� �� ���j �����i�� �� ���j�Ƃ����ƁC��������n�C�����O�C�����O
�@�A�`3���n�C�`2���n
�@�@�́@�` ���i��ij�j���i��'1�C��'2�C��'3�j �����ŁC��'1�C��'2�C��'3�́C��ep�D���C��1����2���n
�@�@��1��tr�`����11�{��22�{��33�C 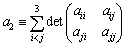
pr)�i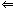 �j�ɂ��ẮC�@�͒��ڑ�����C�A�́C�b�g�d�ɑ�����Đ����B
�j�ɂ��ẮC�@�͒��ڑ�����C�A�́C�b�g�d�ɑ�����Đ����B
�i�ˁj�ɂ��ẮCProp�V��Cor���g����
�@�́Crank�`��3�^2���Crank�`��1�@�@����āC����
�A�́Crank�`��2���Crank�`��2�@�@����āC�����@�@�@��
�@���L�̋�̓I�ȍ\����́C�@��rank�`��1���C�A��rank�`��2���C��|����Ƃ����B
�@�@�̗�F 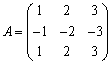
�@�A�̗�F 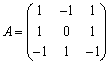 �@���́@
�@���́@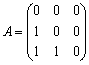
�T�C�܂Ƃ� �@�|����̐i�W�[
(1)�@���߂́C���k�̎���ɉ����邽�߂́w����q�x�ł��������C2���̐����s��ł͎��܂炸�C�\�z�ȏ�ɐ��^�㐔�w�̗̈�ɓ��荞��ł��܂����B��������C��w�ŗ��C�����͂��ł��邪�C�{���ɂ킩���Ă��Ȃ����Ƃ�Ɋ����Ȃ���̌����ł������B�Ⴆ�CProp�W�́˂�pr)�́C�wFrobenius�̒藝�x���瓱���Ă����Ƃ��낪�C�����̓�r�����@���珕�����C���̏������������B�܂�CProp�W�́˂�pr)�̒ʂ�C�`p�̌ŗL�l�̓�p�ł���̂ŁC����Cor�Ƃ��āwFrobenius�̒藝�x���t�ɂ����������B
�Ƃ�����C�T�C�U�̃e�[�}�𒆐S�Ƃ��āC�w����q�x�̓��ʂȏꍇ�Ƃ��āC�b�g�d����̍\���C�p��s��܂ŋ�̓I�ȍ\�����ł������Ƃ͈�̎��n�ł������B�wJordan�̕W���`�x�ɔ��W����w�p��s��̕W���`�x�ɂ��ẮC�����̉ۑ�Ƃ������B
(2)�@���^�㐔�w�́C1���I���O�Ɋ������ꂽ�Ƃ����B���̒��ŁC�w����q�x�͓���ȑ��݂ŁC���̒�`����B���Ɉ����C���܂�Ƃ肠�����Ă͂��Ȃ��̂��c�O�ł���B�����I�ɈՂ�������Ƃ������Ƃ��낤���C����I�ɂ́C���k�����������悤�ɁC�\�����̉��l�������Ă���B1�̎w���@�Ƃ��āC�w����q�x�k�ɋ�̓I�ɍ\�������钆�Ńx�N�g���̓��ς�������@���l������B�܂��C���^�㐔�w���̂��̂ɂ��Ă��C�w�ǂ̃e�L�X�g���s���瓱�����Ă��邪�C�{�e�̂悤�Ɂw����q�x���瓱�����C��Ƀx�N�g����Ԃ��w�сC�s����ɂ��邱�Ƃ��l������B����I�ɂ́C�܂��܂����J���̕���ŁC�傢�ɊJ���̗]�n���c���Ă���Ǝv���B
(3)�@���ꂩ��̊�b�����C�Ƃ�������ōŋ߂̎��͔��M���Ă���B���k����̎���C�^��͍���́w����q�x�Ɍ��炸���푽�l�ł��邪�C����ɖ����ɉ����Ă������߂ɂ́C��b�����͕K�v�s���ł���ƍl���邩��ł���B���k�Ƌ��Ɋw�ԋ��t�ł��肽���Ǝv���B
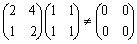
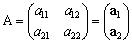 �@�@
�@�@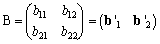
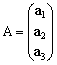 �@�@
�@�@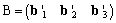
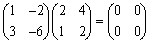 �@�@
�@�@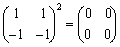
 �@�����s��`�C�a��2���܂���3���̂�����ɂ��Ă��C�w����q�x�ɂ��ẮC�����������Ă��邪�C���ꂾ���ł͎c�O�Ȃ���\���I�ɂǂ��Ȃ��Ă���̂��킩��Ȃ��B
�@�����s��`�C�a��2���܂���3���̂�����ɂ��Ă��C�w����q�x�ɂ��ẮC�����������Ă��邪�C���ꂾ���ł͎c�O�Ȃ���\���I�ɂǂ��Ȃ��Ă���̂��킩��Ȃ��B �`�C�a��3���̂Ƃ�
�`�C�a��3���̂Ƃ�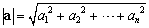 �����̐�Βl�C�����=a1b1�{a2b2�{�c�{anbn���������̓��ςƒ�`����ƁC
�����̐�Βl�C�����=a1b1�{a2b2�{�c�{anbn���������̓��ςƒ�`����ƁC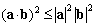 ���
���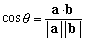 �Ȃ�Ƃ���`�ł���̂ŁC������������̂Ȃ��p�Ƃ����B������������O�̂Ƃ��C���Ƃ��͐����Ƃ������ۂ��ŕ\���B
�Ȃ�Ƃ���`�ł���̂ŁC������������̂Ȃ��p�Ƃ����B������������O�̂Ƃ��C���Ƃ��͐����Ƃ������ۂ��ŕ\���B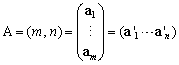 �Ƃ����Ƃ��C
�Ƃ����Ƃ��C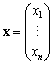 �ɑ���
�ɑ��� �v���ŕ\���B
�v���ŕ\���B �����藧�Ƃ͌���Ȃ��B�����ŁC����q�����߂Ē�`����B
�����藧�Ƃ͌���Ȃ��B�����ŁC����q�����߂Ē�`����B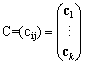 �@��i���um�@1���͂�����
�@��i���um�@1���͂�����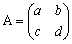 �Ƃ����ƁC�b�g�d�́Cdet�`���O���
�Ƃ����ƁC�b�g�d�́Cdet�`���O���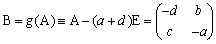
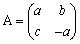 �@�@�������C��2�{�������O
�@�@�������C��2�{�������O
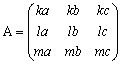
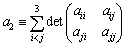
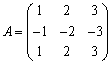
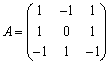 �@���́@
�@���́@