命題Ⅰ,|F(x)|>G(x) 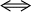 F(x)>G(x)またはF(x)<-G(x) F(x)>G(x)またはF(x)<-G(x)命題Ⅱ,|F(x)|<G(x) 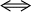 -G(x)<F(x)<G(x) -G(x)<F(x)<G(x)命題Ⅲ,|F(x)|=G(x)  F(x)=G(x)またはF(x)=-G(x) F(x)=G(x)またはF(x)=-G(x)
|
命題Ⅰ,|F(x)|>G(x) 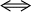 F(x)>G(x)またはF(x)<-G(x) F(x)>G(x)またはF(x)<-G(x)命題Ⅱ,|F(x)|<G(x) 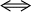 -G(x)<F(x)<G(x) -G(x)<F(x)<G(x)命題Ⅲ,|F(x)|=G(x) 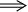 F(x)=G(x)またはF(x)=-G(x) F(x)=G(x)またはF(x)=-G(x)
|
(1) 12年前の同僚との平行線
当時ある生徒が、上記の『絶対値不等式』の公式(?)を使って問題を解いてきたので、『この公式は公には認められていないので、使ってはいけない』と指導したところが、同僚のA教諭から『この公式は、成り立つので使っていいのだ』と抗議を受けた。どうやら生徒の方は、この同僚から公式の伝授を受けていたようだ。これに対して、私の方は『訳の分からない公式を使って生徒に解かせても本当に解けたとはいえないので、たとえ成り立つとしても好ましくない』と反論した。同僚も『正しいものは使かわせて良い』と譲らなかった。今にして思うと、当時どうして論証しなかったか悔やまれるところである。
(2) ネット上の議論
最近偶然、ある同僚とこの公式について話題になった。『集合と論理』により検証を試みた結果、真偽について明快な形で証明できたので、この結果をまず校内の数学科の先生方にみてもらった。そこで、本校の南 俊明教諭から『このテーマなら、かつてネット上で話題になった』と指摘されたので、早速検索したところ、『数実研』の有力中心メンバーの中村先生、真鍋先生、早苗先生であることがわかった。そこで、この中の早苗先生(新川高校)にお願いし、『ネット上の議論』についての資料を入手した。
さて、当時の『ネット上の議論』を要約すると、次のようになると思う。
① 中村文則先生(当時新川高校)による『まなぶ法』(←中村先生が命名)
|2x-3|≦x+1, |3x-1|>x+3, |x-1|≧2x+3
を例にして、『絶対値不等式の公式』を使うことは許されるか?
② 真鍋先生(篠路高校)
|ax+b|<cx+d 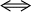 -(cx+d)<ax+b<cx+d
-(cx+d)<ax+b<cx+d
は、成り立たないのではないか。
理由は、一般に、-(cx+d)<cx+dとはならないから。したがって、
CASE1:cx+d≧0
CASE2:cx+d<0
の場合分けが必要である。
③ 中村文則先生による『まなぶ法の限界』
|A|>B 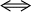 A<-B,B<A |A|<B
A<-B,B<A |A|<B 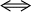 -B<A<B
-B<A<B
は、Bの正負に関わらず成立するので、A,Bが整式でも同様に成り立つと思う。
④ 早苗先生(当時稲北高校)
|A|>B 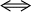 A<-B,B<A |A|<B
A<-B,B<A |A|<B 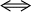 -B<A<B
-B<A<B
において、『A<-B,B<A』を『A<-BまたはB<A』
『-B<A<B』を『-B<AかつA<B』
と、それぞれ言い換えておく必要がある。
⑤ このほかにも、宮田先生(山梨市)、近岡先生(富山県高岡西高校)、富田さん(稚内市)、古川先生(SEG)から、いろいろと示唆に富む指摘があった。
命題Ⅰ,|F(x)|>G(x) 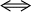 F(x)>G(x)またはF(x)<-G(x) F(x)>G(x)またはF(x)<-G(x) 命題Ⅱ,|F(x)|<G(x) 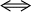 -G(x)<F(x)<G(x) -G(x)<F(x)<G(x)命題Ⅲ,|F(x)|=G(x) 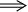 F(x)=G(x)またはF(x)=-G(x) F(x)=G(x)またはF(x)=-G(x) |
(1) 結論から言えば、Ⅰ,Ⅱ,Ⅲとも成立。(Ⅲの逆、![]() については、不成立である。)
については、不成立である。)
証明のポイントは、集合から∀x(任意のx)をとってきてfix(固定)することによって、F(x)、G(x)を『ある1つの定数』とすることにある。当然、このようなxが存在しないとき、その集合はφ(空集合)にほかならない。
一方、集合を使わずに『命題の論理』で詰めた場合、慣れてないと混乱する。論理の真偽について確認しておきたい。例えば、『φ(空集合)⊂(任意の集合)』を論理で言い換えると、pが偽のときqの真偽に関わらず『p
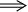 qは恒真命題』である。
qは恒真命題』である。
(2) 以下、各命題の真偽について、論証する。
命題Ⅰ 『|F(x)|>G(x) F(x)>G(x)またはF(x)<-G(x)』の証明
A≡{x∈R:|F(x)|>G(x)}
B≡{x∈R:F(x)>G(x)またはF(x)<-G(x)}
とおくとき、A=Bを示せばよい。
A∋∀xに対して、|F(x)|>G(x)
CASE1:F(x)≧0のとき、F(x)>G(x) ∴x∈B
CASE2:F(x)<0のとき、-F(x)>G(x) つまり、F(x)<-G(x) ∴x∈B
いずれにしても、x∈B よって、A⊂B ①
B∋∀xに対して、F(x)>G(x)またはF(x)<-G(x)
F(x)>G(x)または-F(x)>G(x)
ここで、|F(x)|≧F(x)かつ|F(x)|≧-F(x)より
|F(x)|>G(x) よって、A⊃B ②
①,②より、A=B よって、命題Ⅰが成立 □
上の証明を、『ネット上の議論』に関連づけるため、別証明する。
命題Ⅰの別証明
R∋∀xに対して、 G(x)について場合分けすると、
(ネット上で稚内の安田さんも指摘している通り、以下のCASE2が少しわかりにくくなる。F(x)、G(x)を『ある1つの定数』とすることを再確認したい。)
CASE1:G(x)≧0のとき、
|F(x)|>G(x) F(x)>G(x)またはF(x)<-G(x)は成立する。
CASE2:G(x)<0のとき、
|F(x)|>G(x) F(x)>G(x)またはF(x)<-G(x)は成立する。
(∵p、qがともに真のとき、『p qは恒真命題』)
よって、いずれにしても命題Ⅰが成立 □
trivialな例として、
命題Ⅳ 『|x|>-2 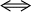 x>-2またはx<-(-2)』は、A=B=R(実数全体)となって成立する。
x>-2またはx<-(-2)』は、A=B=R(実数全体)となって成立する。
命題Ⅱ『|F(x)|<G(x) 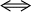 -G(x)<F(x)<G(x)』の証明
-G(x)<F(x)<G(x)』の証明
C≡{x∈R:|F(x)|<G(x)}
D≡{x∈R:-G(x)<F(x)<G(x)}
とおくとき、C=Dを示せばよいが、
『命題Ⅰ,|F(x)|>G(x)F(x)>G(x)またはF(x)<-G(x)』は、>を≧で置き換えても全く同様に成立するので、この両者の補集合からすぐにC=Dが従う。 □
上の証明で論証的にはすっきりするが、間接的証明のためその途中がみえなくなくなってしまうのが残念である。そこで、改めて直接証明する。証明は、集合を使ってC⊂D, C⊃DよりC=Dとする方が明快だが、『ネット上の議論』にも関連づけるため、敢えて別証明する。
命題Ⅱの別証明
R∋∀xに対して
CASE1:G(x)>0のとき、|F(x)|<G(x)-G(x)<F(x)<G(x)
CASE2:G(x)≦0のとき、|F(x)|<G(x)-G(x)<F(x)<G(x)
(∵p、qがともに偽のとき、『pqは恒真命題』)
よって、命題Ⅱが成立 □
trivialな例として、
命題Ⅴ『|x|<-2 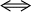 -(-2)<x<-2』は、C=D=φ(空集合)となり成立。
-(-2)<x<-2』は、C=D=φ(空集合)となり成立。
命題Ⅲ『|F(x)|=G(x) 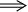 F(x)=G(x)またはF(x)=-G(x)』の証明
F(x)=G(x)またはF(x)=-G(x)』の証明
P≡{x∈R:|F(x)|=G(x)}
Q≡{x∈R:F(x)=G(x)またはF(x)=-G(x)}
とおくとき、P⊂Qを示せばよい。
P∋∀xに対して、|F(x)|=G(x)
CASE1:F(x)≧0のとき、F(x)=G(x) ∴x∈Q
CASE2:F(x)<0のとき、-F(x)=G(x)よりF(x)=-G(x) ∴x∈Q
いずれにしても、P⊂Q
よって、命題Ⅲのが示された。 □
これも、『ネット上の議論』にも関連づけるため、別証明する。
命題Ⅲの別証明
R∋∀xに対して
CASE1:G(x)≧0のとき、
|F(x)|=G(x)F(x)=G(x)またはF(x)=-G(x)
CASE2:G(x)<0のとき、
|F(x)|=G(x)F(x)=G(x)またはF(x)=-G(x)
(∵pが偽のとき、qの真偽に関わらず『pqは恒真命題』)
いずれにしても、命題Ⅲのが示された。 □
Remark1
命題Ⅲの逆、![]() は成立しない。(∵Q∋∀xに対して、F(x)=G(x) または F(x)=-G(x)のいずれにしても|F(x)|=|G(x)|となるが、これがG(x)に等しくなるとは限らないので
は成立しない。(∵Q∋∀xに対して、F(x)=G(x) または F(x)=-G(x)のいずれにしても|F(x)|=|G(x)|となるが、これがG(x)に等しくなるとは限らないので ![]() は不成立。反例は、G(x)<0のときである。)
は不成立。反例は、G(x)<0のときである。)
trivialな例として、
命題Ⅵ『|x|=-2 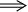 x=-2またはx=-(-2)』は、この逆が成り立たないことは、代入によってすぐわかる。
x=-2またはx=-(-2)』は、この逆が成り立たないことは、代入によってすぐわかる。
命題ⅠⅡⅢが成立すると認められたので、系を紹介する。
命題ⅠⅡⅢの系
(1) |F(x)|>|G(x)| 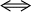 -F(x)<G(x)<F(x)または F(x)<G(x)<-F(x)
-F(x)<G(x)<F(x)または F(x)<G(x)<-F(x)
(2) |F(x)|=|G(x)| 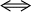 F(x)=G(x)またはF(x)=-G(x)
F(x)=G(x)またはF(x)=-G(x)
系の証明
(1)について
|F(x)|>|G(x)|F(x)>|G(x)|または F(x)<-|G(x)| (∵命題Ⅰ)
|G(x)|<F(x)または |G(x)|<-F(x)
-F(x)<G(x)<F(x)またはF(x)<G(x)<-F(x) (∵命題Ⅱ)
(2)について
については、Ⅲを繰り返し使えばよい。
については、代入による。 □
Remark2
系1は、『かつ』と『または』の分配則によって、次と同値となる。
『-F(x)<G(x)またはF(x)<G(x)』かつ『G(x)<F(x)またはG(x)<-F(x)』
Remark3
以上の中で、F(x)、G(x)を実数値関数としてきた。つまり、連続性や微分可能性などの他の条件は一切仮定していないので、各命題は任意の実数値関数F(x)、G(x)について成立する。
また、x∈Rとしたが、次元を拡張してx=(x1、x2、…、xn)∈Rn(n次元ユークリッド空間)としても成立する。このとき、F(x)、G(x)は、多変数の実数値関数となる。このときの写像は、『Rn → R』である。
(1) この『絶対値不等式』を生徒に紹介すべきか?
これについての回答は、明らかに『否』であろう。『ネット上の議論』でみられる通り、我々教師自身が混乱してしまうことを、生徒に使わせるべきではない。ただし、生徒の実態に応じた指導を考えれば、上記の論証が理解でき、その公式の使い方まで含めて指導できる一部の生徒については、この限りではない。そうでない大部分の生徒に対しては、
『G(x)=a(正の定数)のとき』
に限って、指導しておくのが無難である。このときは、命題Ⅲの逆、![]() も成立している。これが、『公式』として認められているのは周知の通りである。
も成立している。これが、『公式』として認められているのは周知の通りである。
(2) 生徒に紹介すべきでないもう1つの理由
仮にこれを生徒に紹介した場合、どういうことが起きるか想像してほしい。生徒は、公式の意味がわからずに、ただ答えを出す『計算マシーン』と化してしまうばかりか、特にG(x)<0のときに至っては混乱してしまうはずである。混乱しないために、絶対値の場合分けがあるわけだから、これでは本末転倒である。
命題Ⅳ~Ⅵのtrivialな例は、論証上はtrivialであっても、教育上はtrivialどころか、大混乱を引き起こしてしまう。つまり、論証上のtrivialとは、わかっている人だけにとってのtrivialであって、そうでない人にとってはtrivialでないわけである。この両者間には、相当な開きがあることを認識しておく必要がある。
例えば命題Ⅵ『|x|=-2 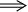 x=-2またはx=-(-2)』は、論証上成立するが、仮に問題『方程式|x|=-2を解け。』と与えられたら、当然答えは『xは解なし』であって、『x=-2またはx=-(-2)』とすべきでないことは言うまでもない。
x=-2またはx=-(-2)』は、論証上成立するが、仮に問題『方程式|x|=-2を解け。』と与えられたら、当然答えは『xは解なし』であって、『x=-2またはx=-(-2)』とすべきでないことは言うまでもない。
(3) 絶対値の指導目的は何か
数学教育の目的の1つに、生徒自身が自ら考えて自分の答えを出すという点がある。絶対値の指導目的は、絶対値の意味や必要性を理解させ、その使い方では絶対値についての場合分けをきちんとさせることである。途中を無視して答えのみを出させることは、目的と手段の履き違えである。
実際、|x|=±xという指導を受けた生徒の中には、|2|=±2、|-2|=±(-2)、という誤用がよくみられる。
絶対値が出てくると、生徒は理解しにくいのですぐ公式に頼って機械的に解こうとしてしまう。そうではなく、時間をかけてこれを数学的にきちんと指導するのが我々数学教師の責任ではないか。
(1) 教育現場における基礎研究
最近の私は、このような立場でいろいろと発信している。つまり、我々数学教師は、あまりに教育現場に偏り過ぎ基礎研究を怠っていないかというシグナルである。この私のスタンスに対して、ほかの同僚から『そんなことをして現場で何の役に立つのか』と冷ややかにみられたりもするが、今回のテーマはそれに応えるという意味で好例であったと思う。今回の論証も、基礎研究という立場に立っていたからできたものと確信するからである。論証する場合、具体的に考えるより、抽象的に処理した方が良い場合がよくあるが、今回の場合もまさにそのひとつであった。
論証は、数学にとって生命線のようなもので、これを欠いたりあいまいにしては、いかなる主張も認められない。ところが、現場では目の前にいる生徒に対してどう対処するかばかりに気をとられ、この精確な論証を怠ってしまう傾向にある。
冒頭にあげた同僚のA教諭との平行線もそうであった。生徒ならともかく、我々数学教師自身が論証を怠って、訳のわからない公式を生徒に紹介することだけは避けたいものである。
(2) 数学における玄人(プロ)と素人(アマ)
数学者の間では、近代数学、現代数学の発展があまりにも急激なために、過去の定理を全て吟味しきれずに、そのまま認めてしまって最新の研究をしている。例えば、解析系ではルベーグ積分の『有界収束定理』の証明を知らなくても、ソフト面でその定理が使えれば事足りるわけである。しかしこれは玄人(プロ)の世界で許されることであって、それを素人(アマ)が模倣するときは『大変なしっぺ返し』に合うことを覚悟しなければならない。 この中にあって、我々数学教師は玄人(プロ)でも素人(アマ)でもない、いわば準玄人(セミプロ)ともいうべき存在である。その意味で、玄人(プロ)と素人(アマ)の間の橋渡しをしていく立場にあるのではないかと思う。
(3) 今後の進展
繰り返すが、本テーマを通して、基礎研究の大切さを改めて痛感した。今回の絶対値不等式のように、高校数学では基礎研究の面から論証が不十分だったり、未確認のものがほかにもある。もし数学的論証のないまま現場で扱うのであれば、それは、『理論なき実践』である。乱暴なたとえをするならば、『建築力学の理論なくして、高いビルを建てるようなもの』で危険極まりない。
今後も現場における具体例について、理論的、実践的な基礎研究を積み重ねて、ひとつのものに集約していきたいと思っている。この点で、北海道の高校数学教育界をリードする『数学教育実践研究会』は、熱心かつ良心的な数学教師の理論的・実践的な研究集団で刺激的である。今後とも指導、助言を仰いでいきたい。
最後に、本レポート作成に当たって、新川高校の早苗先生には資料の提供をはじめ、有益な助言を頂きました。改めて、ここに感謝申し上げます。
命題ⅠⅡⅢの証明では、『集合による論証』と並行して『論理による論証』をしたので、ここで、論理の真偽表について確認したい。 (真をT,偽をFとする)
| p | q | p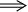 q q |
pかつq | pまたはq | p |
pまたは |
|
| T | T | T | T | T | T | T | T |
| T | F | F | F | T | F | T | T |
| F | T | T | F | T | T | F | F |
| F | F | T | F | F | T | T | T |
上表の結果から
『p 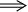 q』と『
q』と『![]() またはq』、『p
またはq』、『p ![]() q』と『pまたは
q』と『pまたは![]() 』 ・・・*
』 ・・・*
の真偽がそれぞれ一致しているので、それぞれ同値関係にある。
したがって、『p 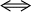 q』は、[『
q』は、[『![]() またはq』かつ『pまたは
またはq』かつ『pまたは![]() 』]と同値である。
』]と同値である。
さらに分配則により[『pかつq』または『![]() かつ
かつ![]() 』]であるから、 p,qがともに真のとき、『p
』]であるから、 p,qがともに真のとき、『p 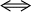 q』は真。p,qがともに偽のとき、『p
q』は真。p,qがともに偽のとき、『p 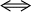 q』は真。
q』は真。
これは、『p 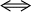 q』を、[『p
q』を、[『p 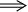 q』かつ『p
q』かつ『p ![]() q』]と考えても同様の結果となる。
q』]と考えても同様の結果となる。
※ 上記の*を使うと何かと便利である。例えば、お馴染みの
『∀ε>0,∃δ>0,s.t.|x-a|<δ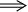 |f(x)-f(a)|<ε』を否定するとき、*を使って『∀ε>0,∃δ>0,|x-a|≧δまたは|f(x)-f(a)|<ε』と言い換えてから否定すると、『∃ε>0,∀δ>0,|x-a|<δかつ|f(x)-f(a)|≧ε』
|f(x)-f(a)|<ε』を否定するとき、*を使って『∀ε>0,∃δ>0,|x-a|≧δまたは|f(x)-f(a)|<ε』と言い換えてから否定すると、『∃ε>0,∀δ>0,|x-a|<δかつ|f(x)-f(a)|≧ε』