生徒は，小・中・高と12年間，算数・数学と付き合ってきて，大部分は学習に疲れ，数学のとらえ方がよじれ，ますます数学を嫌う心理状態に陥っています．さらには，偏差値がそれに追い打ちをかけています．そこで，授業をしていても，“とんな難しいことをやるのだろうか”“この難しい授業は，どこまで果てしなく続くのだろうか” という，やるせなく，あきらめにも似た気持になっているようです．数学を教える者として，どのようにしたらやる気が出て，生徒の目が輝くのだろうかと，常々考えています．そして．授業する側の責任の重さに，日々苦しんでいます．

　生徒が，体育大会・学校祭・部活などで夢中かつー生懸命に取り組んでいるときの目が輝いている姿を見るとき，これを授業に少しでも導入することができるならば・・・・・・と思う昨今です．

　手作業，パソコンと，波の実験をニ次曲線(楕円)の導入教材として工夫して，数学に新鮮なイメージ・興味・関心を持たせ，ひいては，意欲，ファイトを燃やして取り組むことができるようになればと考えた一つの試みです．

　ニ次曲線(楕円)の持っている性質について気付かせるのが授業のねらいです，

1. 中心を記した円を印刷した紙を使って
   1. 上記の紙を配布し，ハサミで円周を切り取らせる．
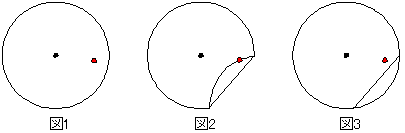
   2. 中心以外に任意の点を記入させる(図1)．
   3. 円周がその任意の点に重なるように折る(図2).
   4. 折り目の線分上に鉛筆で線を引く(図3)
   5. �B�Cの作業を何回も繰り返す．
   6. 直線でどんな図形が描けたか確認する．
   

   　多くの生徒か非常に丁寧な作業をし，楕円ができることを確認しました．図4は生徒の作品例です．

   　
   図4

   　中心に近い所に任意の点を取ったため，できる図形が円だという生徒が1人だけいました，

2. パソコンを用いてのシミュレーソョン
   1. OHPを用いて包絡線で楕円を描く(写真1，写真2)

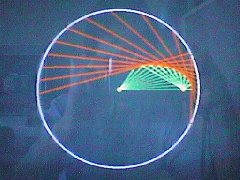
      写真1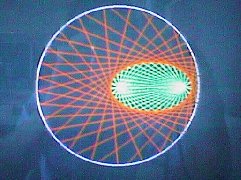

      写真2

3. なぜ，楕円があらわれたのか
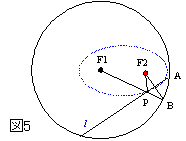
   1. 折り返してできた線分F₁P+F₂Pは半径F₁Bで一定であることを生徒に気付かせる(図5).
   

4. パソコンを用いてのシミュレーション

   　OHPを用いて，F₁P+F₂P=一定(半径)であることを確認する(写真3，写真4)．

   写真3

   写真4

5. 実際に確かめてみよう
   1. アクリルの楕円の容器をOHPの上にのせ水を入れる．
   2. 焦点上にスポイトで水滴を垂らす．そこで起こる波が，他方の焦点に収束することを見せる．ここで，感嘆と拍手が起きた．

　この授業で，直線でニ次曲線(楕円)が描けることを，自分自身が紙を折るという作業を通して認識し，なぜ楕円になるかを考え，そこに潜む性質を理解できたようです．

　夢中になって未知なるものに興味・関心を抱く心は，まだまだ失われていないことを授業を通して実感しました．生徒も二次曲線(数学)をうんと身近に感じてくれたならば，今回の授業は，大成功だったと思います．

　偏差値に左右される教育現場で働く者として，授業そして教授するということを原点にもどって考え直す必要があると考えます．

　今回の授業で，本校数学科の瀬戸先生にプログラムを組んでいただき，浜野・田中両先生にアドバイスをいただきました．紙面をかりてお礼申し上げます．