導入教材の工夫で，数学に新鮮なイメージ・興味・関心を持たせ，ひいては，意欲，ファイトを燃やすことが出来るようになるのではないか。〈はじめに〉
生徒は，小中高と，12年間，算数，数学と付き合ってきて，多くは，学習に破れ，数学のとらえ方が，よじれて，もつれて，嫌う心理状態に陥っている。さらには偏差値がそれに追い打ちをかけている。そこで授業をしていても，今日は，“どんな難しいことをやるのだろう”“この難しい授業は，どこまで果てしなく続くのだろう”と，やるせなく，あきらめにも似た，気持ちになっている。数学を教える者として，どのようにしたら，やる気が出て，生徒の目が輝いてくれるだろうかと，常々考えている。また，教授する側の責任の重大さに，日々，苦しんでいる。
その時，生徒が，スポーツ，遊び，など，一生懸命に取り組んでいる時の目の輝いている姿を見る時，これを，授業に，少しでも導入することが出来たならば・・・と考える。
〈数列の導入を考える〉
導入教材の工夫で，数学に新鮮なイメージ・興味・関心を持たせ，ひいては，意欲，ファイトを燃やすことが出来るようになるのではないか。
数学を勉強しても，直接世の中で生きてゆくには，その知識は直接役に立たないという意識が強く存在する。そこで，パズルゲーム「ハノイの塔（ディスクピラミッド）(図)」を数学Aの数列の導入教材として用い，数列の法則の存在に気づかせることが，ここでのねらいである。
 | →生徒に配られたもの 工作用紙2枚 |
ゲームのルールを説明します。
(1)1回に1枚ずつ動かす。
(2)小さいものの上に大きいものをのせることは出来ない。
(3)すべてを別の場所へ移し換える。
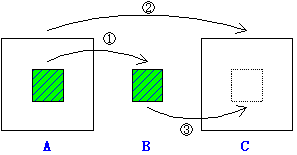
「これは6枚あります。わかりやすく説明するために，2枚で考えてみましょう。・・・それでは，プリントを見ながら2枚の移動をやってみよう。」
＊何故6枚にしたかというと，予想を立て，実際のゲームに少し時間をかけた方がよいと考えたためである。4，5枚では，すぐ出来てしまうし，7，8枚では時間がかかりすぐて，あきらえてしまう生徒が生まれる可能性があり，1時間(50分)で，ある程度ゲームを楽しむことが出来て法則（やり方）のイメージ化が，解決できる範囲と考えて，ここでは6枚とした。机の上に，プリントを図のように置き3つの場所をきめてやって見よう。最低何回で出来るか。それではやって見よう。
| A | B | C |
|
出来た生徒は手を上げて，回数を云って下さい。黒板に書きます。（期間巡視をしながらゲームのやり方を迷っている生徒にゲームの説明をする。）
| 1枚のとき （ １ ）回 2枚のとき （ ３ ）回 3枚のとき （ ７ ）回 4枚のとき （ ）回 ＊4枚位より答えが色々出て来るようになる。 5枚のとき （ ）回 6枚のとき （ ）回 ・・・・・・ ・・・・・・ 9枚のとき （ ）回 |
「少し，何か法則のようなものを見つけ出して考えてみよう。」
| 1回 | 3回 | 7回 | 15回 | 31回 | 63回 [ヒントとして回数の差をとることを考える。] | |||||
| ∨ | ∨ | ∨ | ∨ | ∨ | ||||||
| 2 | 22 | 23 | 24 | 25 | ||||||
| ↑ | ↑ | ↑ | ↑ | ↑ | ↑ | |||||
| 1枚 | 2枚 | 3枚 | 4枚 | 5枚 | 6枚 |
1+2+22+23+24+25=1+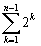
=63 （階差数列）
| 1枚 | 1回+1 | =2 ［ヒントとして回数に1を加えることを教える］ | ||
| 2枚 | 3回+1 | =22 | ||
| 3枚 | 7回+1 | =23 | ||
| 4枚 | 15回+1 | =24 | ||
| 5枚 | □+1 | =25 | ||
| 6枚 | □+1 | =26 | → 26-1 | =63 |
| ・・・・・・ | ||||
| ・・・・・・ | ||||
| 9枚 | □+1 | =29 | → 29-1 | =511 |
| ・・・・・・ | ||||
| n枚 | → 2n-1 | （等比数列） | ||
(ⅰ)(ⅱ)については，ほんの少しのヒントで，生徒が，法則性を見つけ出した。
「さらに，ゲームの構造から，なぜこのような法則が出て来るかを考えてみよう。」
| 1枚のとき | 1回 | 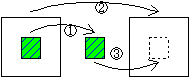 | 1= | 1回 |
| 2枚のとき | 3回 | 1+1+1= | 3回 | |
| 3枚のとき |
| 3回 1回 3回 | ||
| 4枚のとき |
| 7回 1回 7回 | ||
| 1枚 | 1回 | =1 | =1 | =1 |
| 2枚 | 3回 | =1+1+1 | =1+2･1 | =1+2･1 |
| 3枚 | 7回 | =3+1+3 | =1+2･3 | =1+2(1+2) |
| 4枚 | 15回 | =7+1+7 | =1+2･7 | =1+2(1+2+22) |
| 5枚 | 31回 | =15+1+15 | =1+2･15 | =1+2(1+2+22+23) |
| 6枚 | 63回 | =31+1+31 | =1+2･31 | =1+2(1+2+22+23+24) |
| ∨ ∨ ∨ (i) (ii) (iii) ｜ ｜ └一番下の上に移動する回数 ｜ └一番下の移動回数 └下から2番目までの移動の回数 | ||||
「どう計算しても63回が答えのようです。正解の生徒がいますか。自分の予想とはどうでしたか。もう一度，友達，家族の人とやってみてください。」
〈まとめ〉
この授業を通して，数列（数学）が，ぐーんと近くに感じてくれたことと思う。それは，ゲームを一生懸命に夢中になって楽しんだことから生まれる。数列（数学）を有効に使うと役に立ちそうだ，というイメージが出て来る。さらに，そのイメージから，よしやってみようという意欲が出て来て，数列の理解を助けることになる。その意味では，このパズルはよい教材である。
また，先生方の間でも，“掛算・九九・分数が出来ない，だから，三角関数，指数･対数関数，さらには微分積分まで教えるこてゃ出来ないし，仮に教えたとして，何の意味があるのか”という話が，よく聞かされる。高校生が，三角関数，指数･対数関数さらには，微分積分まで学ぶ意義は大きい。それは，その教材の持っている本質的意味が大きいからである。教師も含めて，大人は，数学の学習は経験的に，単線（メインパス）でしか成立しないと思い込んでいるからではないか。迂回路（バイパス）があってもおかしくない。東洋の数学，なかでも中国の数学・和算などを学ぶことによって，色々興味ある発想で西洋の数学には見られない新しいアプローチが可能になる。今後は，単線の教材の指導方法ではなく，複線で考え，様々なバイパスを見出していって，子供達の興味，関心の持てる数学の教材づくりをしなければいけないと考える。
〈最後に〉
以上のように、筆者は授業を通して数学が「わかり」，そして「できる」ようになることが共に達成されねばならない，と考えている。「わからなくてもできる」では困るのである。
我が高校でも，今の時期には授業のために教室へ入っていくと受験・偏差値にー喜一憂していることが手に取るように伝わってくる。したがって，「わかること」またその「楽しさ」などどこ吹く風といった感があり，教師がそのための準備をしていってもなかなか生徒に伝わらないことを実感する。彼らは，試験で「できる」ようになるための学習を求めているわけである。
「割り算は，ひっくり返してかける」したがって，口/6=口×9などとする例が生じる。あるいは，60+4=20と言い張る子供もいる。スピード・アップ，能率アップを重視したいわゆる「できるようになるための教育」では，結局のところ「できない」生徒をも多く生み出すことになろう。
答を20と言い張った子どもは，周りからも「何故，素直に答を変えようとしないのか」として「変わった子」のレッテルがはられることになる。恐ろしいことである。
幸い，父親に，じっくりと問われ，その原因も明らかとなり，救われた。60を6と10に分解する。その上で①6+4=10 ②10+10=20としていたのである。つまり，位取りの理解が完全に欠けていたことがわかる。しかし，子どものつまづきの原因はわからないまま，「できない子」のレッテルがつけられかねない危惧を常にはらんでいるように思えてくる。つまり，子どもが自ら「落ちこばれて」いつたのではなく，教える側が「落ちこぼして」しまうのである。教える立場の責任の重大さを感じる。
無作法，不器用，醜男その上要領が悪く，名もなく，力もなく，金もなく，しかも女にもてない，世間からバカだと言われる，うらぶれた，なさけない男，もちろん勉強は嫌いで偏差値は無いに等しかったろう渥美清演ずる「寅さん」は，現代のスピードと効率を重んじるエリート社会から見れば，落ちこぽれだ。しかし，何故人気があり何処に魅力を持っているのか，偏差値で測ることの出来ないものが存在することを教えている。
偏差値の中で仕事をしている私たちに，授業，教授することを，根源にもどって考え直す必要があると痛感している。
教育研究(札幌学院大学教職課程運営委員会編昭和61年)に寄稿したものに加筆したものです。