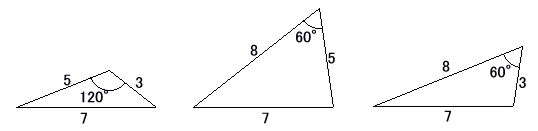
丂壓偺嶰妏宍傪幍屲嶰乹俈俆俁乯嶰妏宍偲屇傃丄妎偊偰偟傑偆偲條乆側栤戣夝朄偵栶偵棫偮丅儅乕僋側傜寁嶼晄梫丄婰弎幃側傜梋尫掕棟偺嵟弶偺幃傪彂偄偰偛傑偐偡丅帪娫抁弅偵偼傕偭偰偙偄偱偁傞丅
丂帡偨傛偆側傕偺偵乽柤屆壆乿乮俈俆俉乯嶰妏宍偑偁傝丄墌偵撪愙偡傞巐妏宍偺娫戣摍偱幍屲嶰嶰妏宍偲偲傕偵傛偔搊応偡傞丅傑偓傜傢偟偄偺偑乽柤傒傖乿乮俈俁俉乺嶰妏宍偱丄柤屆壆偵帡偰偄傞偺偱柤屆壆曎晽偵惗搆偵尵偭偨偑姰暻偵偼偢偟偰偟傑偭偨丅

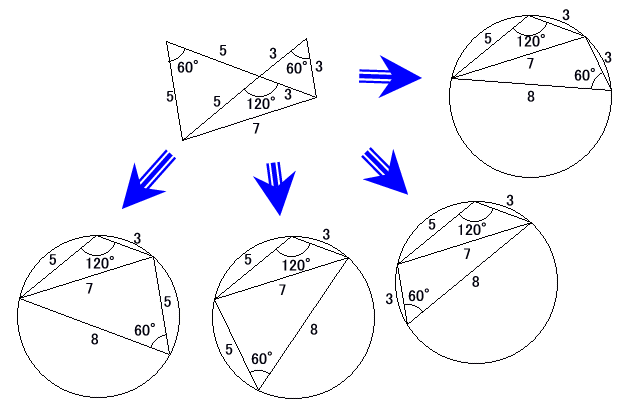
丂傑偨丄侾曈偺挿偝偑俈偺惓俁妏宍傪挘傝崌傢偤傞偙偲傕偱偒傞丅乮俋俉僙儞僞乕捛帋乯
| 倎丗倐丗們 | 亖侾俋丗俆丗侾俇 | (値亖係) |
| 丂 | 亖俈丗俁丗俆 | (値亖俆) |
| 丂 | 亖侾俁丗俈丗俉 | (値亖俇) |
| 丂 | 亖係俋丗係俆丗俁俀 | (値亖俉) |
A亖俇侽亱偺偲偒摨條偵丂丂倎丗倐丗們亖(値2亄俁)丗(値2亄俀値亅俁)丗係値
| 倎丗倐丗們 | 亖俈丗俆丗俉 | (値亖俀) |
| 丂 | 亖侾俋丗俀侾丗侾俇 | (値亖係) |
| 丂 | 亖侾俁丗侾俆丗俉 | (値亖俇) |
| 丂 | 亖侾俁丗侾俆丗俈 | (値亖俈) |
| 丂 | 亖俇俋丗俈俈丗俁俀 | (値亖俉) |
| 丂 | 亖俈丗俉丗俁 | (値亖俋) |
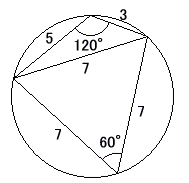
丂傛偭偰丄師偺傛偆側墌偵撪愙偡傞巐妏宍傪嶌傞偙偲偑偱偒傞丅
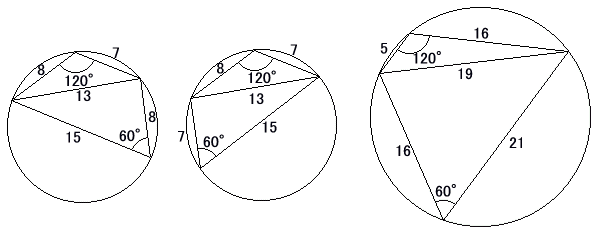
丂偙偙偱捀妏偑俇侽亱偺曽偺嶰妏宍傪摍媟戜宍偵側傞傛偆偵挘傝崌傢偣偨偑丄峫偊偰傒傟偽
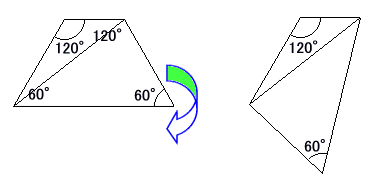
偺宍偺摍媟戜宍偼偦傕偦傕墌偵撪愙偡傞偟丄懳妏慄偱丏擇偮偺嶰妏宍偵暘偗偰丄偦偺曅曽傪嵍塃懳徧偵傂偭偔傝曉偣傁丄偄偔傜偱傕係曈偑惍悢偺撪埪巐妏宍(俇侽亱侾俀侽亱)傪嶌傞偙偲偑偱偒偦偆偱偁傞丅偙偙偱峫偊偨偺偼丄懳妏慄偺堦偮偑惍悢偵側傞摿庩側応崌偱偁偭偨丅
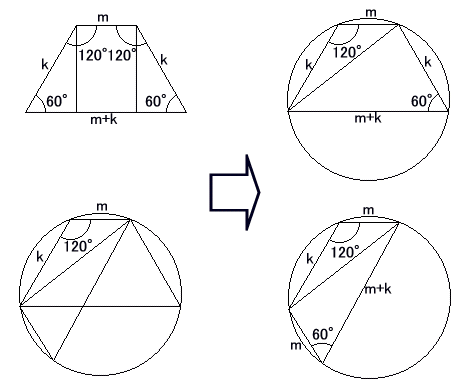
丂梋尫掕棟偵傛偭偰傕丄師偺傛偆偵妋擣偱偒傞丅
丂丂丂丂倣2亄倠2亅俀倣倠cos120亱亖倣2亄倣倠亄倠2
丂丂丂丂(倣亄倠)2亄倠2亅俀(倣亄倠)倠cos60亱亖倣2亄倣倠亄倠2
丂丂丂丂倣2亄(倣亄倠)2亅俀倣(倣亄倠)cos60亱亖倣2亄倣倠亄倠2
|
栤丂墌偵撪愙偡傞巐妏宍俙俛俠俢偼丄俙俛亖俆丆俠俢亖俙俢亖俁丆俙亖侾俀侽亱傪枮偨偟偰偄傞丅偙偺偲偒 乮侾乯俛俢偺挿偝傪媮傔傛丅丂丂乮俀乯俛俠偺挿偝傪媮傔傛丏 |
乲埫嶼夝乴
丂乮侾乯幍屲嶰嶰妏宍偩偐傜丄俛俢亖俈
丂乮俀乯侾俀侽亱傪偼偝傓曈偺挿偝偑乮俁丆俆乯偺偲偒丄俇侽亱傪偼偝傓曈偺挿偝偼
丂丂丂丂丂丂乮俁丆俁亄俆乯傑偨偼乮俆丆俁亄俆乯
丂丂丂偱偁傞丏偙偺応崌偼慜幰偩偐傜丄俛俠亖俉
乲晛捠偺夝朄乴
丂乮侾乯梋尫掕棟偐傜丂俛俢亖俈傪摫偒丄
丂乮俀乯俛俠亖倶偲偍偄偰梋尫掕棟傪傕偲偵俀師曽掱幃傪夝偄偰丂俛俠亖俉
|
栤丂巐妏宍俙俛俠俢偑墌偵撪愙偟丆 丂丂丂丂俙俛亖俁丆俛俠亖侾丆俠俢亖俁丆俢俙亖係 偱偁傞偲偒丆佢俙偺戝偒偝傪媮傔傛丏 |
乲埫嶼夝乴
丂丂墌偵撪愙偡傞摍媟戜宍偱偁傞偐傜丆佢俙亖俇侽亱
乲晛捠偺夝朄乴
丂丂佢俙亖兤偲偍偄偰丄梋尫掕棟偲曗妏偺掕棟傪梡偄偰妏搙傪媮傔傞丅