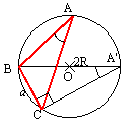
 �i�`���s�p�̏ꍇ�j | 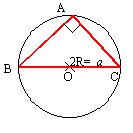 �i���p�̏ꍇ�j |  �i�݊p�̏ꍇ�T�j |  �i�݊p�̏ꍇ�U�j |
| �O�ډ~�̔��a�q��ϋɓI�ɗp����ؖ� �@�P�@���ʂ̏ؖ��i�P�j �@�Q�@�����b�g�̒����ɒ��ڂ����ؖ� �@�R�@���S���_�A���a�q�̉~��p������@ �@�S�@�}�`�Ǝ���p������@ | �u�`�@�`�v�͎��̊��z�ł� �@�`�������~�����Ƃ��낪�s���` �@�`�����I�ƈ�u�����B�������ʓ|�` �@�`�{�p�������ɋ�����Ȃ��` �@�`�}�`�Ǝ��͐��U�����藝�͐��T�` |
| �q���l�����Ȃ��ؖ� �@�T�@���ʂ̏ؖ��i�Q�j �@�U�@�ʐς̌�������̏ؖ� �@�V�@��Q�]���藝����̏ؖ� �@�W�@��P�]���藝����̏ؖ� �@�X�@�w�I�ؖ� | �@ �@�`���̐}�͌�X�܂Ŏg���鏊�ɖ��́` �@�`�N�₩�����}�`�I�Ɉ������������` �@�`���Ƃł͈����Ȃ��������[���` �@�`����͖�����ɋ߂��` �@�`���w�j�̕����ɂ̂��Ă��܂����` |
| �����藝�̎��Әb�� �@���~�[�̒藝 �@���w�j�Ɛ����藝 �@�ӂ肾���ɖ߂� | �@ �@�`���߂Ēm��܂����` �@�`���ׂ�Ɠ���` |
�P�@���ʂ̏ؖ��i�P�j
 �i�`���s�p�̏ꍇ�j |  �i���p�̏ꍇ�j |  �i�݊p�̏ꍇ�T�j |  �i�݊p�̏ꍇ�U�j |
�Q�@�����b�g�̒����ɒ��ڂ����ؖ� �i�T ���ʂ̏ؖ�(�Q)�̕ό`�j
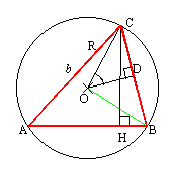 �p�`���s�p,�p�a���s�p�̏ꍇ
�p�`���s�p,�p�a���s�p�̏ꍇ�@���@�b�g����sin�a�@�Ƃ��Ă��悢
�@���Asin�`=sin�ڂb�n�c���b�c/�b�n �Ƃ��Ă��悢�B
�@���B�b�n���������ĉ~���Ƃ̌�_���d�Ƃ���
�@�@����Ƃ��Ȃ��݂̐}�B���̎������b�`�g�Ɓ��b�d�a�Ƃ������œ��l�ɂł���B
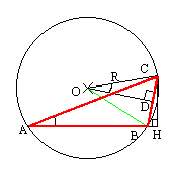 �p�`���s�p,�p�a���݊p�̏ꍇ
�p�`���s�p,�p�a���݊p�̏ꍇ�@���C�b�g����sin�i180���|B�j�ł��悢�B
�@���Dsin�`=sin�ڂb�n�c���b�c/�b�n �Ƃ��Ă��悢
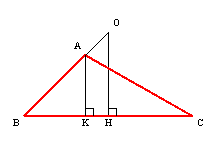
�R�@���S���_�A���a�q�̉~��p������@
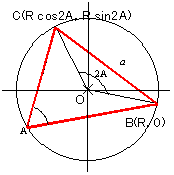
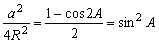
�S�@�}�`�Ǝ���p������@
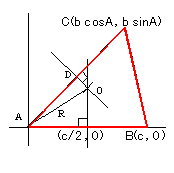
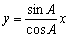
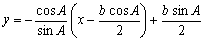
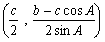
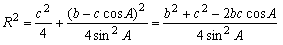
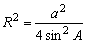
�T�@���ʂ̏ؖ��i�Q�j
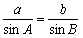
�U�@�ʐς̌�������̏ؖ�
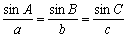 �@�@�@���@
�@�@�@���@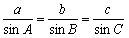
�V�@��Q�]���藝����̏ؖ��P�j
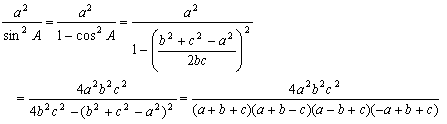
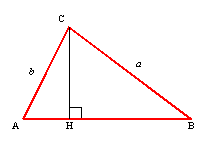
�@�p�a�A�b�ɂ��Ă����l�̌��ʂɂȂ邱�Ƃɂ���ďؖ��ł���B�܂����̎��̍ʼnE�ӂɒ��ڂ���ƁA�O�ډ~�̔��a�q���������ŕ\���Ă�����A�w�����̌����������ċ����[���B
�@������Q�l�����Q�j�ɂ�����ݼޭ��1799�N�ɗ]���藝���琳���藝�����Ƃ���B
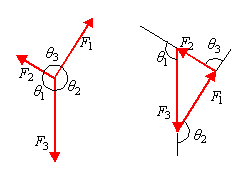
�W�@��P�]���藝����̏ؖ��R�j
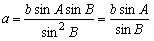 �@�@���@
�@�@���@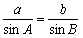
�X�@�w�I�ؖ��@֯۰�߂ɂ�����O�p�@�̊�b��������ڷ���ǽ(1436-1376)�̏ؖ��S�j
���~�[�̒藝�T�j
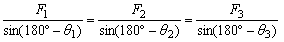
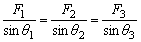 �@�@�i���~�[�̒藝�j
�@�@�i���~�[�̒藝�j���w�j�Ɛ����藝
�@�܂萳���藝�́h�q�h�ɂ́A�Ñ�M���V������p������Ă����h�V���w�̓���Ƃ��Ẳ~�Ɗp�Ƃ̌����Ƃ������j�I�ȈӖ������h�������Ă�����̂ł͂Ȃ����B�܂�����̂悤�ɎO�p�`�̉�@�̂��߂ɐ����藝�����p�����̂́A�]���藝�̒a���ƂƂ��ɂP�T�`�P�U���I�̃��[���b�p����Ƃ����Ă���B
�@�i���w�j�͉����[���āA���ׂ�ɂ͑����ȘJ�͂��K�v���Ƃ킩���܂����B��肪��������ĉ������B�j
�@���͂���܂ŁA�����藝���O�p�`�̉�@�̂��߂̌����ƍl���Ă����̂ŁA�ˑR�̊O�ډ~�̔��a�q�ɂ��ؖ��ɂ͏�X��a���������Ă����B�ł���Ώȗ����Ă��܂������Ƃ��v���Ă����B�����藝�������鎞�ɂȂ��ē˔@�o���������Ƃ����Ԃɏ����Ă����O�ډ~�̔��a�q�́A�O�p�@�̗��j�Ƃ��̐����ߒ��Ƃ�����ɓ`�����ϋ����[���L�[���[�h�Ɠǂ݂Ƃ邱�Ƃ��ł���B
�ӂ肾���ɖ߂�
�@����Ȏ��Ȗ��������A�����m��Ȃ��Ŕ��R�Ƌ����邱�ƂƁA���낢��Ȃ��Ƃ�m������ŋ�����̂ł͑����Ȃ�Ƃ��Ⴄ�͂��ł���B
�@���x�����藝�������鎞�́A�q���g��Ȃ��ŏؖ������コ�肰�Ȃ��q�ɐG��邩�A����Ƃ����j�����Ȃ��畁�ʂɏؖ����邩�A�����Ɠ����Ɋy���݂ł���B
| �P���Ԗ� | �����藝�̏ؖ� | ���j�����Ȃ���u���ʂ̏ؖ��P�v�ŏؖ� |
| �Q���Ԗ� | �����藝�̊m�F | �O�p��̕\�������Đ��������Ƃ��m�F |
| �R���Ԗ� | �����藝�̗��p | �ӂ̒��������߂� |
| �S���Ԗ� | �����藝�̗��p | �p�̑傫�������߂�i���p�̘a��180���j |
| �T���Ԗ� | �܂Ƃ߂Ɖ��K | �O�ډ~�̔��a�A����щ��K |
| �P�j�A��`���� | �킭�킭�w�Ԑ��w�`�̍l���� | ���i��o�Ŏ� | 1997 |
| �Q�j�ۍ�G������ | ��ڲ��ق̐��w�j�U�A�V | ��|�o�� | 1997 |
| �R�j���w��@���T | �@ | ������ | �@ |
| �S�j�����Lj꒘ | ���w�j | �|���� | 1959 |
| �T�j���c������ | �ЂƂ�ʼn�����O�p�� | ���c�V�ߕ� | 1996 |