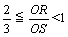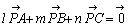 偲偺娭楢傗丆柺愊斾丆廳怱側偳偲偺娭學傪尋媶偡傞偲丆偝傜偵偍傕偟傠偄帠崁偑敪尒偱偒偦偆側梊姶傕偟偰偄傑偡丅扤偐偑偙傟傪尦偵慺惏傜偟偄棤媄傪敪尒偟偨傜偳偆偐嫵偊偰偔偩偝偄丅
偲偺娭楢傗丆柺愊斾丆廳怱側偳偲偺娭學傪尋媶偡傞偲丆偝傜偵偍傕偟傠偄帠崁偑敪尒偱偒偦偆側梊姶傕偟偰偄傑偡丅扤偐偑偙傟傪尦偵慺惏傜偟偄棤媄傪敪尒偟偨傜偳偆偐嫵偊偰偔偩偝偄丅丂悘暘埲慜偺僙儞僞乕帋尡摍偱庡栶偩偭偨偙偺庬偺栤戣偼丆尰嵼偱偼撪愊偍傛傃妏搙忦審偑偮偔側偳丆儊僱儔僂僗傗僠僃僶偺掕棟丆婎慴揑側UFO嶌愴偺傒偱壗偲偐偟傛偆偲偡傞傛傝傕丆暥帤學悢傪梡偄偰楢棫曽掱幃偵帩偪崬傓偲偄偆婎杮揑側夝朄偺曽偑廳梫偱偁傞偲峫偊傑偡丅
丂傑偨丆偙偺棤媄偼尷掕偝傟偨愝掕偺応崌偱偡偟丆帪乆偟偐妶梡偟側偄偺偵埫婰偡傞帠崁偑寢峔偁傝傑偡丅偟偨偑偭偰丆偁偔傑偱嫵巘懁偺専嶼梡丆庯枴梡丆惗搆傪傃偭偔傝庤昳梡丆偲墴偝偊偰丆惗搆偺巜摫忋偵妶梡偡傞帠偵偼廫暘側拲堄偑昁梫偲峫偊傑偡丅巹偼墘廗偺夝摎偺嵺偵乽偒傛偟偺掕棟乿偲尵偭偰暿夝偺堦偮偲偟偰徯夘偟偨掱搙偱愢柧偼偟傑偣傫偱偟偨丅
丂崱夞偼棤媄偺徯夘偱廔傢偭偰偄傑偡偑丆 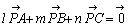 偲偺娭楢傗丆柺愊斾丆廳怱側偳偲偺娭學傪尋媶偡傞偲丆偝傜偵偍傕偟傠偄帠崁偑敪尒偱偒偦偆側梊姶傕偟偰偄傑偡丅扤偐偑偙傟傪尦偵慺惏傜偟偄棤媄傪敪尒偟偨傜偳偆偐嫵偊偰偔偩偝偄丅
偲偺娭楢傗丆柺愊斾丆廳怱側偳偲偺娭學傪尋媶偡傞偲丆偝傜偵偍傕偟傠偄帠崁偑敪尒偱偒偦偆側梊姶傕偟偰偄傑偡丅扤偐偑偙傟傪尦偵慺惏傜偟偄棤媄傪敪尒偟偨傜偳偆偐嫵偊偰偔偩偝偄丅
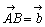 丆
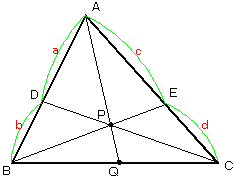
丆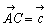 偲偟丆曈俙俛丆俙俠偺撪暘揰俢丆俤傪師偺傛偆偵掕傔傞丅
偲偟丆曈俙俛丆俙俠偺撪暘揰俢丆俤傪師偺傛偆偵掕傔傞丅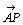 傪
傪 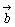 偲
偲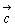 偱昞偣丅
偱昞偣丅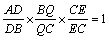
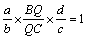 丂傛偭偰丂
丂傛偭偰丂 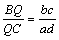
乮俀乯乮侾乯傛傝
丂丂丂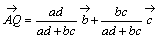
俁揰俙丆俹丆俻偼摨堦捈慄忋偵偁傞偐傜丆
丂丂丂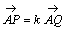
偲偍偔偙偲偵傛傝丆
丂丂丂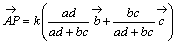
偲側傞丅偙偺幃傪丆
丂丂丂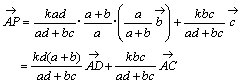 丂丂丒丒丒嘆
丂丂丒丒丒嘆
偲曄宍偟丆揰俹偑慄暘俠俢忋偺揰偱偁傞偙偲偵傛傝丆
丂丂丂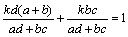
備偊偵
丂丂丂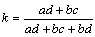
偟偨偑偭偰
丂丂丂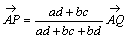 丂丒丒丒嘇
丂丒丒丒嘇
丂丂丂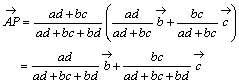 丂丒丒丒乮摎乯
丂丒丒丒乮摎乯
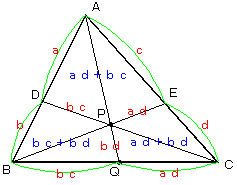
丂傑偨丆嘆偺偟婥偵倠偺抣傪戙擖偟偰丆
丂丂丂俢俹丗俹俠亖倐們丗乮倎倓亄倐倓乯
丂揰俹偑慄暘俛俤忋偵偁傞偙偲偐傜摨條偺寁嶼傪偟偰丆
丂丂丂俛俹丗俹俤亖乮倐們亄倐倓乯丗倎倓
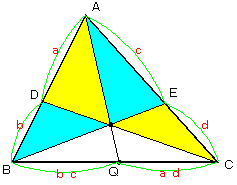 乮侾乯俛俻丗俻俠丂偺斾傪媮傔傞丅
乮侾乯俛俻丗俻俠丂偺斾傪媮傔傞丅| 俛俻丗俻俠亖倐們丗倎倓 |
丂偙偺寢壥傪恾宍揑偵妎偊偰偟傑偆丅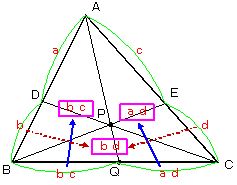 乮俀乯
乮俀乯
| 俢俹偵倐們傪丆俹俤偵倎倓偺抣傪彂偒幨偡丅 |
| 俹俻偵倐倓偺抣傪彂偔丅 |
丂偙傟傕宍幃揑偵妎偊傞丅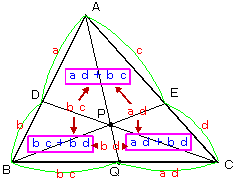 乮俁乯
乮俁乯
俙俹丗俹俻亖乮倎倓亄倐們乯丗倐倓
俢俹丗俹俠亖倐們丗乮倎倓亄倐倓乯
俛俹丗俹俤亖乮倐們亄倐倓乯丗倎倓
偱偁偭偨偑丆
| 偙傟傪塃偺恾偺傛偆偵斾偺抣傪壛偊傞偙偲偵傛偭偰媮傔傞丅 |
丂偙傟偱偡傋偰偺撪暘斾傪娙扨偵媮傔傞偙偲偑偱偒偨丅
丂埵抲儀僋僩儖傪媮傔傞応崌偼丆偙偺斾傪傕偲偵棫幃偡傞偐丆暘曣偺倎倓亄倐們亄倐倓偲暘巕偺倎倓偲倐們傪妎偊偰偍偗偽傛偄丅
丂偱偼搒崌偺傛偄擖帋栤戣偺夝朄偵妶梡偟偰傒傑偡丅
2000.1.29.丂悢幚尋
亂侾亃乵1998杒奀妛墍戝妛乶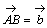 丆
丆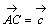 偲偍偔偲偒
偲偍偔偲偒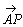 傪
傪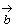 丆
丆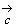 傪梡偄偰昞傢偣丅
傪梡偄偰昞傢偣丅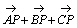 傪
傪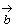 丆
丆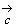 傪梡偄偰昞傢偣丅
傪梡偄偰昞傢偣丅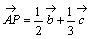 丂乮2乯
丂乮2乯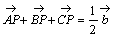 丂乮3乯俙俹丗俹俥亖俆丗侾
丂乮3乯俙俹丗俹俥亖俆丗侾亂俀亃乵1997搶杒戝乶
嶰妏宍俷俙俛偺俀曈俷俙丆俷俛傪偦傟偧傟俁丗侾丆係丗侾偵撪暘偡傞揰傪俠丆俢偲偟丆俛俠偲俙俢偺岎揰傪俹丆俠俢偲俷俹偺岎揰傪俻偲偡傞丅儀僋僩儖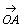 丆
丆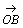 傪偦傟偧傟
傪偦傟偧傟 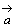 丆
丆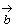 偲偍偔偲偒
偲偍偔偲偒
丂(1) 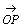 傪
傪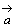 丆
丆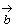 傪巊偭偰昞傢偣丅
傪巊偭偰昞傢偣丅
丂(2) 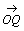 傪
傪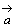 丆
丆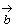 傪巊偭偰昞傢偣丅
傪巊偭偰昞傢偣丅
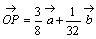 丂乮2乯
丂乮2乯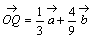
亂俁亃乵1997嬨廈寍弍岺壢戝乶
侽亙倲亙侾偲偡傞丅嶰妏宍俷俙俛偵偍偄偰丆曈俷俙傪倲丗乮侾亅倲乯偵撪暘偟偨揰傪俹丆曈俷俛傪乮侾亅倲乯丗倲偵撪暘偟偨揰傪俻偲偡傞丅慄暘俙俻偲慄暘俛俹偺岎揰傪俼丆捈慄俷俼偲曈俙俛偺岎揰傪俽偲偡傞丅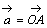 丆
丆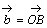 偲偍偔偲偒
偲偍偔偲偒
丂(1) 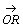 傪
傪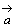 丆
丆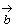 丆倲傪梡偄偰昞傢偣丅
丆倲傪梡偄偰昞傢偣丅
丂(2) 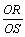 偺偲傝偆傞抣偺斖埻傪媮傔傛丅
偺偲傝偆傞抣偺斖埻傪媮傔傛丅
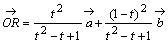 丂乮2乯
丂乮2乯