 |
 |
|
|
いずれも本校の３年生が今春、自宅から学校までの通学経路を描いてきたものである。 地図を描くという作業は、身近な事象を抽象化し、記号的・図的な思考力・表現力が求められる極めて数学的な活動だと云える。距離や方位を定量的にとらえるならばユークリッド的地図となり、量を捨て性質を重視するならばトポロジー的地図となる。
 |
 |
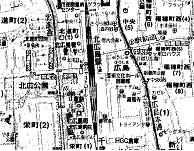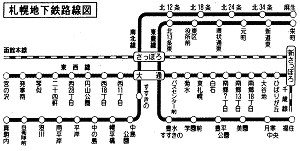| ユークリッド的地図 | トポロジー的地図 |
このように考えるとき、例示したような地図しか描くことのできない生徒は果たして今求められているような
「例えば、自転車に乗る練習はそうですね。百回ころんで乗るのをあきらめてしまえば一生乗れない。しかし、百十回目に乗れるようになったら、もう後は一生乗れる。その百回目と百十回目の間に質的な転化が起こるわけです。それがたまたま起こったのでなくて、その人にとっての量質転化が起きる蓄積の量というのは、たまたま百から百十の間だったということです。だから一個一個の知識についてもこういう量質転化が起きるのだというふうに考えますと、自分はどれくらい勉強すれば、それが一生身につく知識となるかという見通しが立ちます。」したがって、同じ演習をするにしても、どれだけやったら何が身につくのかの見通しを立てた上で、量質転化のラインつまり自転車の乗り方でいうと乗れなかったものがあるところで突然乗れるようになるラインをしっかりと生徒にも判らせるということを教師側が意識し、本年度から次のような取組を試みた。
|
（ア）学習単元を細分化し、その項目毎に演習問題をプリントしたものを２～５分程度で生徒に行わせる。 （イ）その後、赤青緑の三色ボールペンを使い 赤＝すごく重要（客観的） 青＝まあ重要（客観的） 緑＝おもしろい（感覚的） でチェックさせ、周りの席の者と意見交換をさせる。 （ウ）場合によっては「その学習単元の要点を一言で表すキーワードは何か？」と聞いたり、 「問題を創作せよ」といった作問を生徒にさせる。 |
短時間での演習プリントを行うことで演習時間を授業内に確保するためには、内容をシフト化しなければならない。そうすることで生徒は学習内容を段階的にクリアし、いつの間にか目標とする学習内容を習得していくことができる。自動車学校で行われているシェーピングという指導方法と同じである。
縦列駐車なら縦列駐車だけを練習し、クリアしたならその段階を終了。
坂道発進なら坂道発進ばかりを練習する。そうして最終的には車の運転ができるようになるというカリキュラム方法をイメージしてもらえばよい。
さらに、三色ボールペンで色分けし級友達と意見交換することで、互いに触発され学習内容をシェアリングすることができる。
このような授業を実践してみて感じられる教育効果には以下のようなものがある。
（１）結論を先に示す
授業をする際に定理や公式を帰納的に説明するか演繹的に説明するかで、理解度に差が生ずることはすでに知られている。
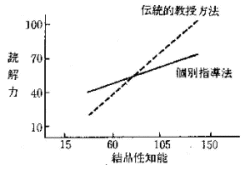次頁の図が２つの教授方法と事後テストの関係をグラフにしたものの一例である。
一寸簡単に説明したい。
（２）生徒の思考力を引き出す発問
定理・公式を先に示し、それを活用できるように数値を代入し、計算するのであれば単なる技術の反復練習にしかすぎない。そうならないために、生徒の思考が揺り動くような発問を吟味し準備するようにしている。
例えば、１０月６日の授業においては次のような発問を行った。
|
3n＝nC0＋2nC1＋22nC2＋…+2nnCn を証明せよという問題において 二項定理 (a＋b)n＝nC0an＋nC1an-1b＋nC2an-2b2＋…＋nCnbn を確認しておき、 「aとbは文字だから、特定の値を代入しても構わないよね。aとbがどういう値ならば、問題にある3nになるだろうか？」 |
タイムリーで本質を突く発問ができたとき、教室は動き出す。
「あ～！判った！！」
「ええっー、どうしてどうして！？」
といった声がわき上がり、教室内はたちまち騒然となり活力が出てくる。
この「ああ、そうか」という瞬間の気持ちが重要である。生徒はこの瞬間変化する自分を自覚し、質的に飛躍する瞬間の自分を知ることになるからである。どのように発問すれば、その教育的価値が生かせるか。毎日の授業において節目節目をスモールステップに分割し、階段を登るときに「ああ、そうか」と生徒が胸を打つ一言が出るような発問をしていこうと心がけている。
たったひとつの発問によって生徒の学習に取り組む姿勢が変わる「きっかけ」となることが本当にある。
さらに、この発問をうまく使うことで、授業においてアシスタント・ティーチャーやティーム・ティーチングの要素も取り入れるようにしている。
詳しくは研究会当日、口頭にて説明したい。
（３）試験問題をひと工夫
近年、大学入試問題でも具体的な素材や事象を扱う問題や、思考力を問う問題が出題されるようになってきた。
| 円周率が3.05より大きいことを証明せよ。 （03年 東京大・前期） |
| 背理法とは何かを 20 字以上 100 字以内で説明せよ。（02年 東京理科大） |
|
次の定理と証明について，以下の問に答えよ。 定理 素数は無限に存在する。 証明 定理が成立しないとすると，素数は有限個である。それらの素数をp1，p2，…，pnとする。このときq＝(p1p2…pn)＋1を考えると，qはp1，p2，…，pnのどれでも割り切れない。(1) したがって，qを素数の積として表したとき，この積に表れる素数はp1，p2，…，pnのいずれとも異なる。これは矛盾である。(2) したがって定理が証明された。 (1) 上のように，結論が成り立たないと仮定して矛盾を導き出すことにより命題を証明する方法を何というか。(00年 北見工大) |
また、テスト問題と授業の関係について９月４日の道立教育研究所における教育講演会で道教育大旭川校の相馬一彦教授は考え方を問う問題が今後も増えてくることを指摘し、「テスト問題を指導に結びつけることが大事であり、授業への生徒の姿勢と方向づけるようなテストづくりをすること」の工夫・改善を求めている。
さらに、北海道において高教研などで何度か講演されている長岡亮介放送大学教授は、本年３月の日本数学会のシンポジウムにおいて
「入試問題を通じて数学者は『数学とは何か』を語っているんだということを忘れるべきではない」
と述べておられるが、これは高校の教師における試験問題も同じ意味を持つ。
どのような問題を出題するかということは、生徒にどのような力を身につけてほしいかということの具体的な表現手段でもある。
そのため愚鈍なる数学教師は無い知恵絞り、砂から水を絞り出すような思いをしつつ、粗悪な計算や技巧に堕することの無いような試験問題をひと工夫している。
次の２題は先日の９月24日に行われた本校１学年の前期期末考査で出題した問題である。
【問題Ａ】サッカーゴール後方には防風林が植えられています。（図１参照） しかし、蹴ったボールがよく飛び出し木に当たるため、環境保護の立場から、木の高さまでの防ぎょネットをはることにしました。木の高さを直接測ることはできません。角度を測定する機器と巻き尺（メジャー）が使えるものとし、どうすれば木の高さを測ることができるのか、三角比の考えを利用して説明しなさい。ただし、目線の高さは考えなくてもよいこととします。 （図１）
|
写真は本校のグランドで生徒をモデルに写したものである。
受験者 356 名中、正解者 193 名、正答率 54.2 % であった。
これは知識偏重型の問題ではなく、解答の糸口を見つけていく部分に力点を置いた解法発見型の問題をねらいとして創った。
sin30°やcos60°の値は求められる－だがそのことがどんな意味を持っているのか、我々の生活にどのように生かされているのか。
そのことを理解せずに、ただ単にパターン化した解法を身につけたり、問題の量をこなしただけのものにはこの問題は解けなかったに違いない。
問われている内容は、どんな教科書にも冒頭で扱われているようなことだけに、基本中の基本とも云える問題なのだが、この正答率の示す意味は大きいと感じる。
tanθを使って説明した者は小数（25人）であり，圧倒的に正弦定理を使って説明した者が多かったのは予想外であった。
他の解答としては
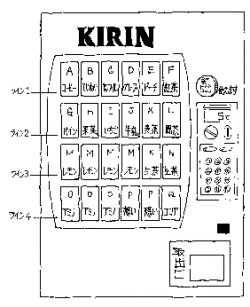
【問題Ｂ】１階玄関横に下図のような自動販売機が設置されたとします。１から４の各ラインには６個ずつの商品が並べられているとき、次の各問いに答えなさい。
|
こちらの方は、オーソドックスな順列と組合せの問題である。題材を本校に設置されている自動販売機としたものであり、その意味では北広島高校オリジナル問題とも云える。
数学は日常の身の回りに沢山あるんだとのメッセージを込めたつもりである。生徒が毎日目にしている自動販売機を数学的にとらえているものがどれくらいいたかは判らないが、試験終了後その自動販売機の前でこの問題の解法を話し合っていた生徒がいただけで収穫はあったと思っている。これを機会に日常の事物を数学というフィルターを通してみることを身につけてくれればと思っている。
出題に当たっては職員室において２名の数学の先生にモニターテストをお願いした。
答案返却時には、出題意図や全体的な傾向、多くみられた誤答例など採点をしていて感じたことを書きまとめ、今後の弱点補強と学習計画も含めた講評として全生徒に配布した。このことは説明責任を果たすという昨今の流れからも意義あることだと考えている。そのプリントには、定型的な処理法を覚えることも勿論大切ではあるが、それだけではなく、自分の力で考える練習を積み、考える力を身につけてほしいとの願いを込め、「平素から充実した数学的体験を蓄積してほしい」と書き結んだ。
|
（ア） 解法をルーチン化し単なる計算力の技巧化に陥る危険性があり、論理的な思考力の育成に課題が残る。 （イ） 発展的な内容、系統的なつながりへの広がりが乏しい。 （ウ） 進度とペースが手探り状態のため三色ボールペンの活用が不規則となる。 （エ） 三色ボールペンでどこに赤をつけるかを全員で確認しておかないと、生徒は瑣末でも判らなかったところ、難しくてできなかったところに赤印を付けたがる傾向がある。 （オ）１校時45分といった短縮授業などのﾓｼﾞｭﾗｰ・ｽｹｼﾞｭｰﾙの対応が難しい |
（ア）、（イ）については「５ 授業と生徒をつなぐ３つのメソッド」のところで、補うための方策について述べた。（ウ）、（オ）についても今後指導実績を重ねることで改善されてくるものと思われる。
この実践を通して気づいたことの１番大きな収穫は前記した（エ）であった。このことは教師側のエアポケットであり、全く迂闊だったと反省している。
どういうことかというと、何題かの問題を前に
「１番大事だと思うところ、試験前にこれだけは確認しておくべきだと思う問題に赤いマークを付けろ」
と指示したとき、生徒は難しい問題、できなかった問題に印を付けたがる傾向があるということである。このことは、とりわけ数学を得意としないタイプの生徒に多く見られる。
この事実に気づいてからは赤いマークについては全員で確認するようにした。さらに、
「単元全体を見渡し、１番大事なところはどこかを見極め、それの習得に多くの時間とエネルギーをかけるんだ。そこのところを押さえておくと、後は単なるバリエーションであることも多い。特別な場合や独特の技法を使うような問題にエネルギーをかけても得はない。何でもかんでも解こうと思って、かえって解かなければならないものを解けなくしてはいけない」
と語るようにしている。
その結果、最近ではようやく半数以上の生徒がこちらの意図を汲み取り、学習単元の本質を示すような問題に赤いマークを付けるようになってきた。しかし、油断するとすぐにテクニカルで難しい問題に意識がシフトしてしまうこともまた事実である。