柔らかな思考力を求めて
北海道岩見沢東高等学校
菅 原 和 良1 はじめに
本校は大正11年に創立された、空知の伝統校として知られる全日制6間口、定時制1間口の普通科高校である。全日制入学者の多くは、上級学校への進学希望を持っており、父母や地域の期待も大きい。
完全学校週5日制や新教育課程の実施が目前に迫り、本校においてもそれらの研究・研修が急務の課題となっている。授業時数の確保や総合的な学習の時間の取り組み、さらには生徒の学力維持・向上、進路実現の達成など、他校同様具体的な課題も少なくない。2 数学的活動を通して創造性の基礎を培う
今回の学習指導要領の改訂では、
- 数学的な見方や考え方のよさや認識
- 活用する態度の育成
という、これまでの学習指導要領の精神を受け継ぐとともに、新たに「数学的活動を通して創造性の基礎を培う」という文言が加えられた。
では、数学的活動とはどのようなことを言うのか。昨年の北数教講習会における文部省教科調査官・吉田明史氏の話では、次の3点でとらえられている。
- 身近な事象を数学化し、数学的な課題を設定する活動
- 数学的に考察、処理し、数学的知識(数学の新しい理論・定理等)を構成する活動
- 数学的知識の意味づけや活用したりする活動
このような数学的活動は、これまでも問題解決能力や考える力といった表現で指導上大切にされてきたものであるが、今回の改訂ではこれらが一層強調されている。
一方、創造性の基礎については、どのように考えればよいのか。
これについては、「多面的にものを見る力や論理的に考える力など、自ら学ぶ意欲、論理的思考力、想像力、直観力、判断力、よさを感じる豊かな感性など、幅広くとらえることができる」と昨年の北数教講習会では説明されていた。
さて、では実際に生徒を指導する場面において、どのようにこの「数学的活動を通して創造性の基礎を培う」ことをしていけばよいのかということになる。
本研究会で何度も研究発表をされている、旭川凌雲高校の奥村稔先生がよく仰有っている「文言や語尾がああ変わった、こう変わったの話は、もういいじゃないか。そんなことより我々は生徒に一体どんなことができるのか。それを考えていきましょうよ」という話が思い出される。
理念は理解できる。しかし、具体的な方策はなかなか見えない。単に問題の解き方を教えたり、内容の理解や技能の習熟にとどまらないためには、どのような指導計画を立て、教材を工夫すればよいのか。
自ら学び、自ら考える力などの「生きる力」を育成することを重視し、教育内容が厳選され、授業時数の縮減がはかられる。その結果、小・中学校から合計200時間以上の内容が高校数学に上がってくることになる。また一方では、従前の学習指導要領における理系の生徒の到達点を守るということも求められている。
本稿では、これらの改訂の趣旨が生かされるよう、実際に試験や授業で生徒に提示した問題を取り上げ、出題の背景にある思想や授業の改善の視点を点描してみたい。3 問題の新しい視点と工夫
ここでは、定期考査などで出題した問題から、代表的なものを9つ取り上げてみた。
ここで取り上げた問題だけが「数学的活動」ではないし、「創造性の基礎を培う」配慮をしたものでもない。ただ、わかりやすい典型的な問題を取り上げることで特色が見えればと思う。(1)直観的な見方や見通しをもつ力
 面積が5c㎡の正方形を、右の1目盛り1㎝の方眼紙に書きなさい。ただし、その4つの頂点は、方眼紙の直線の交点にくるようにすること。 面積が5c㎡の正方形を、右の1目盛り1㎝の方眼紙に書きなさい。ただし、その4つの頂点は、方眼紙の直線の交点にくるようにすること。 |
《解答》
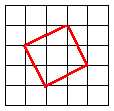
①出題のねらい
この問題は平成5年度の秋田県高校入試問題である。本校では平成7年6月の1年生実力テストで出題した。ちなみに秋田県での正答率は30.9%で、本校では正答者155名、67.1%となっている。
ここでは、論理的な思考力や代数的な処理よりも、一点に集中して考え、直観的に作図の方法を発見することが求められる。
②授業改善の視点
直観力を育てるには、まず思いついたアイデアを自由に出せる雰囲気が授業の中では必要になろう。「笑われるのではないか」と思わせず、どんな突飛なアイデアも奨励したい。また、できたら終わりではなく、他の方法はないか、もっとエレガントな解法はないかと、興味や関心が高まっていくような授業にしたい。そのためには、教師も生徒と一緒になって探求することを楽しむことが大切であろう。さらに、いろいろな解き方やアプローチを出し合うことで、思考力や判断力を磨き合うこともできる。
(2)柔軟に図形を見る目を養い、図形が変化しても保存される性質を見抜く
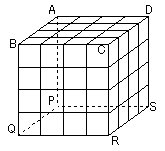 一辺の長さが4の立方体ABCD-PQRSがある。 ただし、2つの正方形ABCD,PQRSは立方体の向かい合った面で,AP,BQ,CR,DSはそれぞれ立方体の辺 である。 一辺の長さが4の立方体ABCD-PQRSがある。 ただし、2つの正方形ABCD,PQRSは立方体の向かい合った面で,AP,BQ,CR,DSはそれぞれ立方体の辺 である。
今、立方体は一辺の長さ1の小立方体に積み木状に区切られているとする。そこで頂点AからRへ小立方体の辺をたどっていくときの最短経路を考える。
(1)頂点Aから頂点Rまでの移動距離はいくらか
(2)頂点Aから頂点Rへ最短経路は何通りあるか
(3)辺BC上の点を通過する最短経路は何通りあるか |
《解答》
 (1)4×3=12
(1)4×3=12
(2)AB方向に長さ1進むことをa、AD方向に長さ1進むことをb、AP方向に長さ1進むことをc、で表すと、AからRへの最短経路は4つのa、4つのb、4つのcを1列に並べることで決まる。よって、
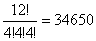
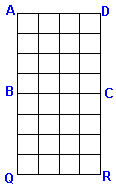
(3)立方体の面ABCDとBCQRを取り出した長方形におけるAからRへの最短経路を考えればよいから、
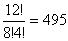
①出題のねらい
この問題は平成10年の9月に、1年生に出題した。237人中、(2)の正解者89人、(3)の正解者21人となっている。授業で1度でも取り上げていれば、また違った数字になったのだろうが、授業では平面図での最短経路までしか扱っていなかったので、生徒は思いの外戸惑ったようである。既習事項である平面での考え方を、どのように適切に活用していけるかを問う問題であり、それらを生徒がどのように利用して解決しようとしているかという、数学的な考え方も評価できる。立体を平面に変形して考える、柔軟な思考力が求められる。
②授業改善の視点
生徒が学習する中で、問題を解きその解法に習熟するだけでは、考える力の乏しいものへと流れてしまう。図形の問題においても、その場面だけで捉えるのではなく、「いつも言えることは何か」、「図を変形しても変わらないことは何か」といったように、一般性をもって考えていくことが大切になる。そのためには、生徒自らが考えて、工夫できることはないかと探求する心をもって授業が展開されることが望まれる。そこで教師は「なぜそうなのか」といった適切な発問や助言を、意識して問いかけることが必要となる。考える力を育てるためには、こうしたことを日頃の授業から配慮すべきであろう。
(3)生活の中の数学と規則性の発見
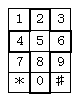 電話機のボタン配列から2,4,5,6,8,0の部分を切り取ってサイコロを作る。このサイコロを2回投げるとき、出る目の和が奇数になる確率を求めよ。 電話機のボタン配列から2,4,5,6,8,0の部分を切り取ってサイコロを作る。このサイコロを2回投げるとき、出る目の和が奇数になる確率を求めよ。 |
《解答》
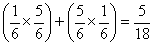
①出題のねらい
滋賀県の高校入試問題からヒントを得て作った問題である。平成7年度の3月学年末考査で1年生に出題した。受験した236名のうち、正解者は111名。正答率は47.0%である。ちなみに滋賀県での正答率は35.4%である。
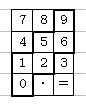
この問題は電話のボタン配列という、身近な数の生活事象から選ばれている。発見した事象や規則を、一般化した問題に応用させることで、他に転用する力を問うている。別の試験で電卓のボタン配列からサイコロを作り出題したこともある。(下図)
 ②授業改善の視点
②授業改善の視点
身近な題材を取り上げることにより、
- 数理的な処理の「良さ」を理解させる
- 数学的な興味や関心を持てるよう工夫する
- 題材のもつ数学的魅力に気づかせる
といったような、学習活動の構成を図っていきたい。(4)日常の出来事を数学的な問題として設定し、整理・発展させていく力を育てる
仲の良い6人グループでカラオケに行くとする。A君はひそかにXさんのことが好きなので、いつもXさんの隣りに座りたいと思っている。このとき次の問に答えよ。ただし、カラオケボックスの席は下図のような横長の長いすとする。
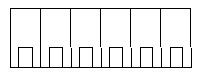 (1)6人の座り方は全部で何通りあるか。 (1)6人の座り方は全部で何通りあるか。
(2)A君とXさんが隣り合って座る場合は何通りあるか。
(3)A君がいつもXさんの隣りに座っていたのでは、みんなにXさんが好きなことが気づかれてしまう。何回に1回の割合で座ればみんなに気づかれないといえるか。 |
《解答》
(1)6!=720
(2)5!×2!=240
(3)A君がXさんの隣に座る確率は、240/720=1/3
つまり、意識しなくても3回に1回は隣りになるのだから、3回に1回の割合で座ればよい。
 ①出題のねらい
①出題のねらい
この問題は埼玉県浦和西高校の太田敏之先生の実践を参考にさせていただいた。平成12年の冬休み明け1月に1年生全員に出題した。(3)がこの問題の核心部分であるが、いきなりの問いかけでは戸惑うだろうと、(1)、(2)を枝問として誘導した。
この問題は右図の一連の流れで示される数学的活動そのものだと捉えられる。しかし、その結果には愕然とさせられた。直接採点をする機会はなかったのだが、採点者によると、「正答者は1クラス10人程度で、正答率はせいぜな考い30%ぐらいだろう」ということであった。もし、「A君とXさんが隣り合って座る確率を求めなさい」と出題されていれば、8割以上が正解したであろう。そのことを考えると、指導してきた生徒がこの程度の変化(応用)に対しきれない弱さには、歯がゆさを感じる。現学習指導要領改訂の際によく引き合いに出されていた、
- 一つの解がx=-3である二次方程式を一つだけ作りなさい。(正当率26%)
- x2-x-12=0 を解きなさい。(正当率77%)
という二例の対比が思い起こされる。②授業改善の視点
生活事象を数学化することは、あまり行われていない。しかし、自然や生活空間の中には、見事な規則性や法則が隠れていたりする。そんな生活事象を素材とする教育開発や蓄積が大切であろう。
生徒の誤答には「1万回に1回ぐらいなら誰も疑わない」といったように、はじめから数学的に捉えることを放棄しているものもあった。このことからも、数学が生活の中でどう役立ち、数学をどう生かすことができるかということを気づかせたい。さらに、数学を身近なものにすることへの配慮と既習事項を組み立てて考えたり、創ったりする「切り拓く力」の育成も十分に考えていく必要がある。そのためには課題学習的なもの、トピック学習的なものを学期に一度くらいは気軽に扱えるようにしていきたいと考えている。
(5)帰納的に考え、見つけ出したきまりをもとに文字を使用して一般化する力を育てる
分母が6の正の既約分数(それ以外約分できない分数)を小さい順に並べてつくった数列を {an} とする。
(1)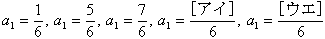 である。 である。
(2)数列 {an} の奇数番目の項,すなわち a1,a1,a1,a1,…を順に並べた数列を {bn} とする。
37/6は数列 {an} の第[オカ]項であり,数列 {bn} の第[キ]項である。
一般に,数列 {bn} の第n項は
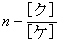
であり,数列 {bn} の初項から第n項までの和は
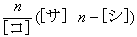
である。
(3)数列 {an} の初項から第100項までの和は[スセソタ]である。 |
《解答》
(1)6と互いに素である自然数を小さい順に並べると
1,5,7,11,13,17,・・・
これが順に,数列 {an} の各項の分子になるから
a4=11/6, a5=13/6
(2)(1)に続けて,6と互いに素である自然数を並べると
1,5,・・・,17,19,23,25,29,31,35,37,・・・
よって,37は13番目の自然数だから,37/6は数列 {an} の第13項である。
次に,奇数番目の自然数だけ並べると,
1,3,13,19,25,31,37,・・・
よって,37/6は数列 {bn} の第7項である。
数列 {bn} は
1/6,7/6,13/6,19/6,25/6,・・・
となり,初項1/6,公差1の等差数列であるから
bn=1/6+(n-1)・1=n-5/6
また,数列 {bn} の初項から第n項までの和は
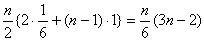
(3)数列 {an} の初項から第100項までには,奇数番目の項が50個,偶数番目の項が50個ある。
奇数番目の第50項までの和は
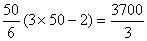
次に,数列 {an} の偶数番目の項を順に並べた数列を {cn} とすると,数列 {cn} は
5/6,11/6,17/6,23/6,29/6,・・・
となり,初項5/6,公差1の等差数列であるから,数列 {cn} の初項から第50項までの和は,
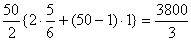
したがって,数列 {an} の初項から第100項までの和は
3700/3+3800/3=2500
①出題のねらい
この問題は、ベネッセの平成11年度第3回進研マーク模試のものである。3年生の受験直後に、2年生の授業で取り上げた。模試での全国正答率は(1)92.7%、(2)41.2%、(3)21.3%となっている。
具体的に数列を書き出し、その中にある2つの数列を考察する問題である。順序よく書き出すことで、帰納的に規則性を発見し、関係を引き出すとともに問題の意味も理解できてくる。具体的に書き出していく操作が有効となる問題である。
②授業改善の視点
数列では多くの生徒が第n項という一般化において戸惑う。そこで、具体的に一つひとつ取り出すことで、その中に潜んでいる関係を自ら発見する喜びや一般化することの有用性を実感させたい。そのためには、日頃から具体的に考え、取り出し、そこから関係を見つけ出すよう、丁寧な指導が大切になる。このような操作の中で、関係に気付いた生徒が次にどう発展していくかを教師は意識づければよいだろう。
(6)図から規則性を適切に読みとる力や数学的に処理する力を育てる
x軸とy軸で分けられた4つの区画を順にA,B,C,Dとする。これに図1のような渦巻きを書き、順に5,7,9…と記入していった。図2のようにA,B,C,Dの各区画の中心から外側に向かい、1層、2層、3層、…としていくとき、次の問に答えよ。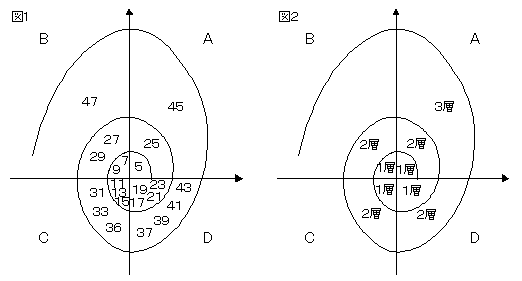 (1)Bの区画で、中心から5番目の層に入る2つの数は何か
(2)2001はA~Dのいずれの区画の中心から何番目の層に入っているか
(3)Cの区画に入る数の和を求めたい
①中心から20番目の層に入っている3つの数の和を求めよ
②中心から20番目の層までの総和を求めよ |
《解答》
(1)初項7,公差20の等差数列の第5,6項目と考えてよいから、87、89
(2)初項をa,公差を20として考えたとき
2001=a+(n-1)・20
2001-a=(n-1)・20
ここでaは
5,7,9,11,13,15,17,19,21,23
のいずれかの数で,nは自然数だから2001-aが20の倍数になるのは,a=21のとき。
このとき n=100 ゆえに2001はDの区画の100層目
(3)
①11+(20-1)・20=391より3つの数は
391,393,395
よって,391+393+395=1179
② (11+13+15)+(31+33+35)+…+(391+393+395)
=(11+31+51+…+391)+(13+33+53+…+393)+(15+35+55+…+395)
=10{2・11+(20-1)・20}+10{2・13+(20-1)・20}+10{2・15+(20-1)・20}
=4020+4060+4100
=12180
①出題のねらい
島根県の高校入試問題をヒントにしたオリジナル問題である。平成12年の3月に文系希望の2年生143人に出題した。簡単な等差数列を渦巻き状の4つの群に分け、その群を周期化したものである。自然数をあるきまりで分類していくとき、その分類の仕方やそこに属する集合の共通の性質を発展させることをねらいとして出題した。この問題では、対象が文系の生徒だったこともあり、あえて一般項まで拡張することはせず、次の2点にウエイトを置いた出題にしたつもりである。
ア 設問に興味を持って取り組み解決しようとする関心・意欲・態度
イ 規則性を見つけ出し、文字式で表そうとする数学的な考え方や表現・処理
最後まで完答した生徒はそれほど多くはなかったが、全ての生徒がこの問題に手をつけ、解こうという意欲を見せていた。試験後「考えて解いていることが楽しく夢中だった」という生徒の感想を得られたことは収穫であった。
②授業改善の視点
まず、一斉授業の中でも一人ひとりが考える時間を確保することが大切であろう。その中で、気づき、発見したものをもとに授業の方向性を示すような指導をする必要がある。また、生徒が自分の見方や考えを持つことと同時に、他人の見方や考え方も認め、比較・検討できるようになることが望ましい。したがって、数学の知識や技能を獲得し、問題が解けるようになることだけを目標にするのではなく、その知識や技能を習得していく課程で様々な考え方に出会い、それぞれの考え方の良さや特徴を感じ取ることができるようになってくれれば素晴らしい。
(7)条件を満たす点の集合を作図やグラフの操作によって表現し、考えようとする力を育てる
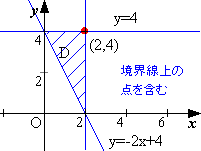
連立不等式2x+y-4≧0<x≦2,y≦4 で表される領域をDとする。次の問に答えよ。
(1)領域Dを斜線で図示せよ。また、境界を含むか、含まないかについて記せ。
(2)領域Dが表す図形を原点のまわりに1回転させたとき、その図形が通過した領域を連立不等式を用いて表せ。 |
《解答》
(1) 
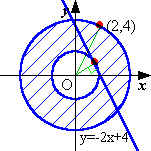 (2)原点から領域Dまでの距離の最大値は,点(2,4)との距離に等しいから
(2)原点から領域Dまでの距離の最大値は,点(2,4)との距離に等しいから
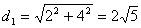
最小値はy=-2x+4との距離に等しいから
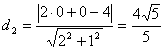
よって 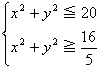
①出題のねらい
神奈川県で実施している県下一斉テストの中の一問として、平成8年11月に出題された問題である。本校では平成10年10月の3年生文系に選択問題の一問として出題し、67名が解答した。見慣れない問題のためか(1)はともかく、(2)の方は正答率が低かった。この問題の解決には、問題文に書かれていることを数学的表現に変えて視覚化することが必要である。しかも単なる作図の手順を覚えていればよいというのではなく、図形が通過した領域を集合としてとらえるという意識を問う問題でもある。内側の円の半径を求めるというイメージができるかどうかという数学的な見方や考え方、さらにはそれを表現する能力が評価できる。
②授業改善の視点
問題解決の際、日頃から図形やグラフを書くことに抵抗をなくしておくことが大切だろう。自分で図を書き、問題の特徴をつかむことで、設問に対する解決の流れが見えてくる。つまり思考力を支える表現力として、図を使いこなせるかがポイントであり、そのような学習をしてきたかどうかが問われているともいえる。このような力を育成するためには、普段の授業の中で「図を用いること」の良さや利便性を生徒に味わせることが大切である。そしてその利便性を味わうことで、生徒は考えを深めていくものと考える。したがって、このような利便性を感得させる授業展開を心がけることが重要であろう。
(8)与えられた条件の依存関係をもとに、直観的な思考力や想像力、的確に表現する力を育てる
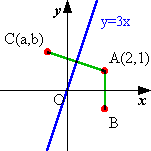
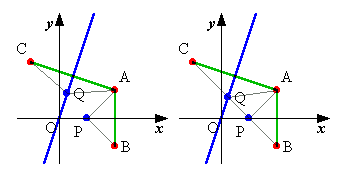
直線 y=3x と点A(2,1)について、次の問に答えよ。
(1)x軸について、点Aと対象な点Bの座標を求めよ。
(2)直線 y=3x について、点Aと対象な点Cの座標を求めよ。
(3)点Cを通り、傾きmの直線の方程式を求めよ。
(4)X軸上に点 P(p,0)をとり、直線 y=3x 上に点 Q(q,3q)をとる。(ただし、p>0,q>0とする)
今、A→P→Q→Aと移動するときの移動距離が最短となるように、点P,点Qの座標をそれぞれ求めよ。 |
《解答》
 (1)B(2,-1)
(1)B(2,-1)
(2)C(a,b)とすると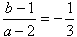 より
より
a+3b=5 ・・・①
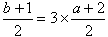 より
より
3a-b=-5 ・・・②
①,②より
a=-1,b=2
ゆえに C(-1,2)
 (3)y-2=m(x+1)より
(3)y-2=m(x+1)より
y=mx+m+2
(4)AQ=CQ,AQ=BPより,AP+PQ+QAが最小となるのはBP+PQ+QCが最小となるとき,つまり一直線上にあるときである。
直線BCはy=-x+1となるから
P(1,0)
点Qはy=3xとの交点だから
3x=-x+1 より x=1/4
よって Q(1/4,3/4)
①出題のねらい
秋山仁監修の著書からヒントを得た問題で、設問を誘導型に枝分けした。平成11年度2年生文系志望者の3月定期考査に出題した。全問完答した生徒は143人中4名であった。生徒にしてみれば、対象点を2つ考えなければならないのが気づきづらく、難しくさせたようである。与えられた点と直線上の動点、さらには対象点に着目し、それらの間の依存関係について考察し、数学的な見方や思考の広がりにより「図形と式」分野の総合的な学習の成果を評価できる問題だと思っている。
②授業改善の視点
問題(大学入試など)があるからそれに合うように授業を改善していくのは、ある面仕方のないことであろう。しかし、授業を改善することで、テストや入試問題が変わるという気概を持ちたい。普通、数学の授業では問題を与え、それを解かせるといった場面が多い。生徒はその問題を「解ければ終わり」という受動的・完結的な学習になりがちである。これを繰り返せば、解法テクニックは身に付くだろうが、未知の問題に直面しての意欲や関心が薄れ、数学的な見方や考え方は育ちにくい。そこで、生徒に問題を自分のものとして受け止められるような課題や工夫を考えたい。自ら取り組み、考え、納得したことであれば、自分の思考の道筋を自分なりの言葉で表現することができる。そのため教師は生徒がもっている情報やアイデアを引き出し、補充、修正して数学の方法にまで高めていくという構えで授業に臨むことが大切である。みんなで考えを出し合い、着想やアイデアを互いに共有することで、思考の練り合いを多く経験させることもできる。これは生徒一人一人が数学的な知識を構成していく上で重要なことであろう。このような点を大切にして、日常の授業を行っていきたいものである。
(9)回す、拡大するという単純な操作の中に潜む数理を論理的に解明しようとする力を育てる
平面上に5点O(0,0),A(1,0),B(3,2),P(1,1),Q(4,5)が与えられているとする。平面における次の3つの操作①,②,③をこの順に行う。
①Oを中心にして正の向きにθだけ回転をする
②Oを中心にしてk倍(k>1)の拡大をする
③OがPに移るような平行移動をする
この結果AがQに移ったとする。このとき、
(1)cosθ,sinθ,kをもとめよ。
(2)上の一連の操作①,②,③の結果Bの移った先の点の座標を求めよ。 |
≪解答≫
(1)複素数平面上で
①はcosθ+isinθをかけること
②実数kをかけること
③は1+iをくわえること
を表すから,AがQに移ることにより
k(cosθ+isinθ)+1+i=4+5i
kcosθ+kisinθ=3+4i
よって kcosθ=3,ksinθ=4
2乗して加えると
(kcosθ)2+(ksinθ)2=25
k2=25
k>1より k=5,このとき
cosθ=3/5,sinθ=4/5
(2)5(cosθ+isinθ)(3+2i)+1+i=(3+4i)(3+2i)+1+i=2+19i
ゆえに、点Bが移った先は点(2,19)
①出題のねらい
平成10年度の京都教育大の入試問題。本校では平成10年10月に3年生文系の選択問題として出題し、62名の者が答えている。一見しただけでは複素数の問題とは気づかないかもしれない。だが、これこそ複素数平面に置き換えることで実にうまくいく問題で、ベクトルの視点を複素数に向けることの大切さがわかる良問だといえる。この問題では、回転する、拡大するといったことで動的にものを見ることでの解決の見通しが必要になる。また、これらの操作によって、点がどのように位置を変え、重なる点との位置関係を論理的に考えることができるかを評価できる。複素数の問題は、多くの分野の知識を問うことができるので、多種多様な解法も期待できる。既習の知識や考え方を総合的に活用し、表現する力や自ら進んで問題を発展させようとする関心・意欲・態度を評価することも可能といえるだろう。
②授業改善の視点
生徒がじっくりと思考するためには、学習内容の関連性を大切にし、系統的な学習の良さを感じることが必要である。基礎的・基本的な知識・理解を定着させることは関心・意欲を高める上で当然必要なことだが、それと同時に、今まで学んだことを次の学習に積極的に活用していく態度も重視されよう。今まで脈絡なく覚えていたものが、ある問題や事象をキッカケに、次々と結合していくとき、生徒は驚きとともに感動を得る。このような体験はそのまま数学科の目標にある「…とともに、数学的な見方や考え方の良さを認識し、それらを積極的に活用する態度を育てる」ことにつながるのではないか。見えなかったものが数学を通し見えてくる感動を、生徒に与えるような授業を行っていきたいとつくづく思う。
4 柔らかな思考力を求めて
学習指導要領が目指す学習指導を、実際に出題した問題を素材に考えてきた。しかし、それ以外にも、例えば「数学を学んで最も感銘を受けた定理の名前とその理由を述べなさい」(東海大学秋山仁教授の提案)というような、自分の考えや判断を記述する問題や逆の考えを求めたり、関係を洞察したりする問題も考えられる。
ここでは、少し見方を変えて生徒が柔軟な思考力を身につけるためにはどのような授業展開を心がければよいかを整理してみたい。
(1)「考えて理解する習慣」を身につける
問題を公式にしたがって、機械的に解法を習熟することでは、そこで思考力が止まってしまう。そうではなく、
・なぜそうなのか
・他の考えはないのか
といったように、生徒がいつでも考えられるようにしたい。いわば、答えを出した後も考え続けられるようにしたいということである。
そのためには、教材の本質をつくタイムリーな発問が不可欠だと思っている。(2)質の高い問題意識を育てる
教師が提示する問題は、いつも操作的・発見的で生徒の意欲・関心を引き出すわけではない。むしろ、生徒側の気付きや疑問、こだわりから学習活動を展開していけるような授業づくりが必要であろう。
生徒の持っている情報やアイデアを引き出し、それを元に授業の進むべき方向を定めることがあってもいいのではないか。自分の考えが広く、深くなければ、他者の考えの良さや特徴も感じることはできないが、そのことはつまり、自分の視野や思考が広くなることで見えなかった問題が見えてくるということでもある。
結局は数学教育を通して人を育てているということだろうか。前出の吉田明史氏は「数学の内容を習得させるということにとどまらず、内容の指導を通して生徒にどういう資質や能力を身につけさせようとしているのかを研究しておくことが重要だ」と述べている。
生徒に問題意識を持たせるということは、視野を広くさせることであり、それは柔軟な思考力へつながる小径でもあるという気がしている。
(3)挑戦する場を授業に取り入れる
挑戦するということは、単に問題に対する取り組みのことではない。
遅れがちな生徒には、今どんなことをやろうとしているのかを問うことも挑戦であり、進んでいる生徒には、なぜその方法でよいかを自問することも挑戦である。答えが出て安心している生徒に、これはどんなことを意味しているの?と問いかけることもできるだろう。
数学では抽象的な内容の理解が求められるから、この概念形成のために乗り越えなければならない壁がある。これを越えて達成するのは、生徒自らの力に頼るしかない部分もある。
5 まとめ
9つの問題を取り上げ、知識記憶型やパターン学習ではない、数学的な良さを発見し、応用することへのアプローチを考えてきた。
とはいっても、授業ではほとんど説明→例題→練習問題という形で進んでいることも否定できない。しかし、そんな中でもエッセンスとして数学への魅力を持たせる問題や教材、発問を工夫し、数学が社会や文化に果たしている役割に触れさせることができないかと試みてきたつもりである。
あらためて考えるとき、「数学的活動を通して創造性の基礎を培う」ということは、人間形成をもっと全面に出したものであり、結局は「教育は人」という想いを強くする。
白状すると、研究発表の依頼を受けてから今迄の実践をまとめる作業をしたのだが、何よりもまず自分自身の授業法や指導観の見直し、向上に役立った。
この機会を与えてくださった高校部会長・佐藤忠雄校長先生ならびに事務局長・長倉伯幸先生に、この場を借りて感謝申し上げ拙稿を閉じたい。
参考文献- 文部省高等学校学習指導要領解説数学編(実教出版株式会社)
- 日本数学教育学会誌第82巻第3号、第81巻題3号
(吉田明史「高等学校数学教育の展望」他) - 根本博編著『新学力観に立つ数学科の高校入試問題と授業改善』(明治図書)
- 学力問題調査研究会編『変わる高校入試問題』(東京書籍)
- 巻久編『Create Math① 高等学校数学指導資料 数学Ⅰ』(みずうみ書房)
- 秋山仁監修『名作から学ぶ奇想天外数学的発想法』(数研出版)
- 中等教育資料平成7年5月号、平成11年7月号、平成12年3月号
- 藤田宏・長岡亮介・長岡恭史共著『大学への数学Ⅰニューアプローチ』(研文書院)
- 高校教育展望平成10年6月号(小学館)
- Information'98.6(旺文社)
- 平成11年度第3回進研マーク模試(ベネッセ)
|
 面積が5c㎡の正方形を、右の1目盛り1㎝の方眼紙に書きなさい。ただし、その4つの頂点は、方眼紙の直線の交点にくるようにすること。
面積が5c㎡の正方形を、右の1目盛り1㎝の方眼紙に書きなさい。ただし、その4つの頂点は、方眼紙の直線の交点にくるようにすること。
 一辺の長さが4の立方体ABCD-PQRSがある。 ただし、2つの正方形ABCD,PQRSは立方体の向かい合った面で,AP,BQ,CR,DSはそれぞれ立方体の辺 である。
一辺の長さが4の立方体ABCD-PQRSがある。 ただし、2つの正方形ABCD,PQRSは立方体の向かい合った面で,AP,BQ,CR,DSはそれぞれ立方体の辺 である。 (1)4×3=12
(1)4×3=12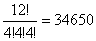
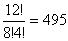
 電話機のボタン配列から2,4,5,6,8,0の部分を切り取ってサイコロを作る。このサイコロを2回投げるとき、出る目の和が奇数になる確率を求めよ。
電話機のボタン配列から2,4,5,6,8,0の部分を切り取ってサイコロを作る。このサイコロを2回投げるとき、出る目の和が奇数になる確率を求めよ。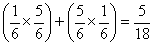
 ②授業改善の視点
②授業改善の視点 (1)6人の座り方は全部で何通りあるか。
(1)6人の座り方は全部で何通りあるか。 ①出題のねらい
①出題のねらい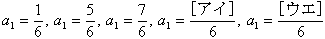 である。
である。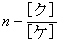
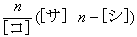
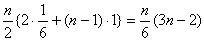
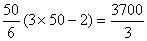
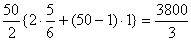


 (2)原点から領域Dまでの距離の最大値は,点(2,4)との距離に等しいから
(2)原点から領域Dまでの距離の最大値は,点(2,4)との距離に等しいから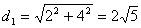
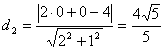
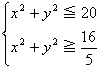
 (1)B(2,-1)
(1)B(2,-1)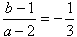 より
より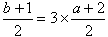 より
より (3)y-2=m(x+1)より
(3)y-2=m(x+1)より