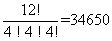通り
| 問題１ １２人を４人ずつ組名をつけない３つのグループに分ける分け方は何通りあるか。 |
数学Ⅰ「場合の数」の難所で有名な箇所です。たいていの教科書では次の方法によっています。
まずこの問題の前に、
| 問題０ １２人を４人ずつ３つのグループＡ ，Ｂ ，Ｃ に分ける分け方は何通りあるか。 |
が紹介されます。問題０の解答は、たとえば同じものを含む順列の考え方によって
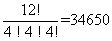通り
そして問題１については 答をｘ通りとして、問題０の答を用いて
ｘ×３！＝34650， ｘ＝5775通り
となります。なぜ ×３！ なのかについて説明しても、場合の数には珍しくいきなり ｘ が登場することもあって、理解できない生徒が多くなりがちです。しかしこの解答が難解であることの原因は他にもありそうなのです。次の問題２をご覧下さい。
| 問題２ ６人を３人ずつ組名をつけない２つのグループに分ける分け方は何通りあるか。 |
教科書流の解答では
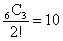通り
です。
実際に生徒６人が二手にわかれて ３ｏｎ３ のゲームをするときのことを考えてみてください。時間に余裕があれば、色々とチーム変えをして遊ぶわけですが、以前のチームと同じチームになってしまってはチーム変えの意味が無い。以前のチームと違うかどうかは、自分の味方２人が以前と違うかどうかで判断するわけです。
つまり自分以外の５人のうちのどの２人が見方かで場合分けは決まり、そう考えると問題２は、5Ｃ2＝10通りです。これは６人のうちの一人の視点、つまり生徒の視点での解答。
一方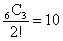通りというのは、６人の外部の人の視点、つまり教師の視点での解答です。どちらがわかりやすいかは一目瞭然でしょう。
問題１にも生徒の視点による解法は使えます。
| 問題１ １２人を４人ずつ組名をつけない３つのグループに分ける分け方は何通りあるか。 |
これなら理解してくれそうです。もちろん教科書流の解答つまり教師の視点での解答の弱点は難解であるという点だけであって、それが優れた手法であることには異論は無いでしょう。たとえば『７人を３人，２人，２人ずつの組名をつけない３つのグループに分ける分け方は何通りあるか。』という問題では、上記の生徒の視点の方法だと場合分けをしなければなりません。教科書流の解答のほうがすっきりとした式になりますね。
教科書流の解答の難解さの原因は、このような視点の違いということの他にもう一つあります。教科書流の解答ではｘ×３！＝34650という式を理解しようとする場合、ｘ が未知であり、さらに ×３！ についても考えなければならないのです。 ×３！ の意味を理解させる（それが問題１のポイントであるわけですが）には、最初に生徒の視点の方法で ｘ＝5775 を求めさせ、さらにそれを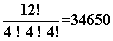
という数と比較させることによって ×３！ という仕組みを理解させる、という方法がわかりやすいでしょう。
以上のように、生徒の視点の方法は、問題を実体験に則した視点で易しく解くことを可能にし、また、教科書流の解答を理解するアシストとしても役立つものです。