| 丂嵗昗暯柺忋偺尨揰傪俷(侽丆侽)偲偡傞丅傑偨倶嵗昗偍傛傃倷嵗昗偑偲傕偵惍悢偱偁傞傛偆側揰傪奿巕揰偲偄偆丅 乮侾乯倲傪惓偺幚悢偲偡傞丅揰俹(亅侾丆侽)傪捠傝丆孹偒偑倲偺捈慄偲扨埵墌倶2亄倷2亖侾偲偺俹埲奜偺岎揰傪俻(倲)偲偡傞丅俻(倲)偺嵗昗傪媮傔傛丅師偵丆侽亙倱亙倲傪傒偨偡俀偮偺幚悢倱丆倲偵懳偟丆慄暘俻(倱)俻(倲)偺挿偝傪媮傔傛丅 侾俋俋俋擭丂搶嫗戝妛丂棟嘥(屻婜) |
丂俹1丆俹2丆俹3丆丒丒丒丆俹n偑慡偰桳棟悢偺偲偒丆偙傟傜偺悢傪巐懃墘嶼偵傛偭偰嶌傝弌偟偨怴偟偄悢傕娷傔偰慡偰桳棟悢偱偁傞丅傑偨桳棟悢偼廫暘偵戝偒側帺慠悢傪妡偗傞偲慡偰惍悢偵側傞丅傑偨帺慠悢偼偄偔傜偱傕戝偒偄悢偑懚嵼偡傞丅偙偺摉偨傝慜偺峫偊曽傪梡偄偰嶌傜傟偨栤戣傪嬶懱揑偵夝偄偰傒傛偆偲巚偆丅
| 丂嵗昗暯柺忋偺尨揰傪俷(侽丆侽)偲偡傞丅傑偨倶嵗昗偍傛傃倷嵗昗偑偲傕偵惍悢偱偁傞傛偆側揰傪奿巕揰偲偄偆丅 乮侾乯倲傪惓偺幚悢偲偡傞丅揰俹(亅侾丆侽)傪捠傝丆孹偒偑倲偺捈慄偲扨埵墌倶2亄倷2亖侾偲偺俹埲奜偺岎揰傪俻(倲)偲偡傞丅俻(倲)偺嵗昗傪媮傔傛丅師偵丆侽亙倱亙倲傪傒偨偡俀偮偺幚悢倱丆倲偵懳偟丆慄暘俻(倱)俻(倲)偺挿偝傪媮傔傛丅 侾俋俋俋擭丂搶嫗戝妛丂棟嘥(屻婜) |
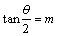 偲偍偔偲
偲偍偔偲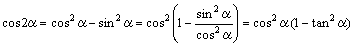
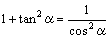 丆丂
丆丂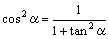
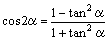
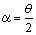 偲抲偔偲俀兛亖兤傛傝
偲抲偔偲俀兛亖兤傛傝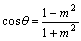
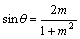 丆
丆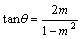
丂曪娷娭學偐傜丆俶伡俻+偼柧傜偐偱偁傞丅
媡傪帵偡丅
丂惓偺暘悢偺暘曣傪倣丆暘巕傪倢偲偡傞丅暘悢偼婛栺偱偁傞偲偼壖掕偟側偄丅偦偟偰倣亄倢亖倠偲偟偰丆倠偺彫偝偄弴偵惓偺桳棟悢傪暲傋偰偄偔偙偲偵偡傞丅偦偺偲偒丆暘曣偼彫偝偄弴偵暲傋傞偙偲偲偡傞丅
丂丂丂倠亖俀偺偲偒偼丆暘悢偼侾乛侾偱偁傞丅
丂丂丂倠亖俁偺偲偒偼丆俀乛侾丆侾乛俀偺俀屄偱偁傞丅
丂丂丂倠亖係偺偲偒偼丆俁乛侾丆俀乛俀丆侾乛俁偺俁屄偱偁傞丅
傛偭偰丆
丂丂丂倠亖値偺偲偒偺暘悢偼丆(値亅侾)乛侾丆(値亅俀)乛俀丆丒丒丒丆俀乛(値亅俀)丆侾乛(値亅侾)
偲側傞丅傑偨倠亖倝偺偲偒偺屄悢偑(倝亅侾)屄傛傝丆倠亖俀偐偨倠亖値傑偱偺暘悢偺屄悢偼
丂丂丂侾亄俀亄俁亄丒丒丒亄(値亅侾)亖値(値亅侾)乛俀
偲側傞丅偙傟傛傝擟堄偺帺慠悢M偵懳偟偰倣亄倢亖M偲側傞暘悢偼丆
丂丂丂嵟弶偺暘悢偑丂(俵亅侾)(俵亅俀)乛俀亄侾丂斣栚
偱偁傝丆
丂丂丂嵟屻偑丂俵(俵亅侾)乛俀丂斣栚
偱偁傞丅傛偭偰擟堄偺惓偺暘悢丂俵1乛俵2丂傕偡傋偰斣崋偑晅偗傜傟偨偙偲偵側傞丅傛偭偰俶偲俻+偼侾懳侾懳墳偱偁傞偐傜丆俶偲俻+偼摨偠屄悢偱偁傞丅偦傟偱偼桳棟悢偺応崌偼偳偆偐偲偄偆偲丆師偺傛偆偵偟偰斣崋傪晅偗偰偄偗偽偡傋偰偺桳棟悢偵斣崋傪晅偗傞偙偲偑偱偒傞丅
丂嬶懱揑偵暲傋偰傒傞丅
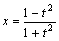
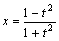 丆倷亖倲(倶亄侾)傛傝
丆倷亖倲(倶亄侾)傛傝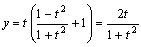
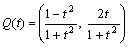 丆
丆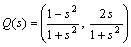
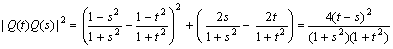
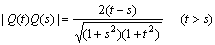
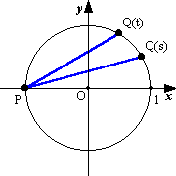 (俀) 佢俻(倱)俷俹亖兝丆佢俻(倲)俷俹亖兝 偲偡傞丅丂
(俀) 佢俻(倱)俷俹亖兝丆佢俻(倲)俷俹亖兝 偲偡傞丅丂 丆
丆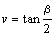 偲偍偔丅嘆傛傝
偲偍偔丅嘆傛傝
丂丂丂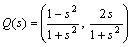 丆
丆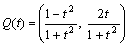
丂丂丂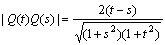
傑偨丆
丂丂丂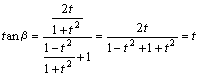
摨條偵 tan兛亖倱 偲側傞丅傑偨丆
丂丂丂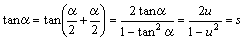
摨條偵
丂丂丂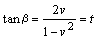
傑偨丆倳丆倴偼嫟偵桳棟悢偱偁傞偐傜倱傕倲傕嫟偵桳棟悢偱偁傞丅(侾)傛傝
丂丂丂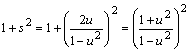
摨條偵
丂丂丂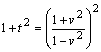
傛偭偰
丂丂丂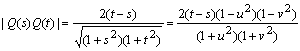
傛偭偰丆倲丆倱丆倳丆倴偑偡傋偰桳棟悢傛傝丆乥俻(倱)俻(倲)乥傕桳棟悢偱偁傞丅
乮俁乯佢俻(倲)俷俹亖兛 偲偟丆 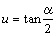 乮桳棟悢乯偲偍偔丅捈慄俹俻偺孹偒傪倲偲抲偔偲
乮桳棟悢乯偲偍偔丅捈慄俹俻偺孹偒傪倲偲抲偔偲
丂丂丂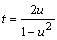
偱偁傞偐傜丆倲傕桳棟悢偱偁傞丅傑偨丆
丂丂丂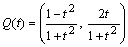
偺奺嵗昗傕偲傕偵桳棟悢偱偁傞丅傛偭偰丆値屄偺桳棟悢傪
丂丂丂侽亙倳1亙倳2亙乧乧亙倳n亙侾
偲偟偰
丂丂丂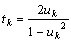
偲抲偔丅倲k偼慡偰桳棟悢傛傝
丂丂丂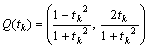
偺奺嵗昗傕偲傕偵桳棟悢偱偁傞丅傑偨丆俀揰俻乮倲k乯丆俻乮倲j乯偺嫍棧偼倲k亜倲j偲偡傞偲
丂丂丂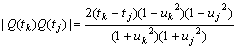
傑偨
丂丂丂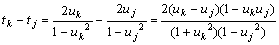
偱偁傞偐傜丆俀揰娫偺嫍棧偼慡偰桳棟悢偱偁傞丅師偵俻(倲k)傪倳k傪梡偄偰昞偡偙偲偵偡傞丅
倶嵗昗偼
丂丂丂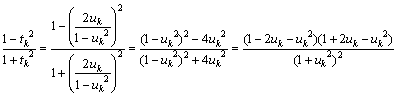
倷嵗昗偼
丂丂丂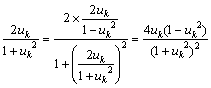
傛偭偰丆倶嵗昗丆倷嵗昗偲傕偵桳棟悢偱偁傞丅
傑偨丆倳k偼惓偺桳棟悢偱偁傞偐傜丆倳k亖倢k乛倣k丂(倣k丆倢k偼帺慠悢)偲抲偔偙偲偑偱偒傞丅
俻(倲k)偺倶嵗昗偼
丂丂丂
倷嵗昗偼
丂丂丂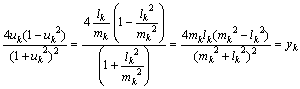
偲抲偔丅摨條偵俻(倲j)偼
丂丂丂倶嵗昗偼丂丂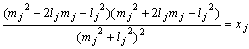
丂丂丂倷嵗昗偼丂丂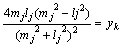
偲抲偔丅傛偭偰儀僋僩儖 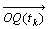 丆
丆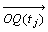 傪偦傟偧傟
傪偦傟偧傟
丂丂丂(倣k2亄倢k2)2 (倣j2亄倢j2)2攞
偡傞偲丆椉儀僋僩儖偲傕暘曣偑栺暘偱偒偰倶嵗昗傕倷嵗昗傕偲傕偵惍悢偵側傞丅偦偺揰傪俛(倲k)丆俛(倲j)偲偍偔丅
丂丂丂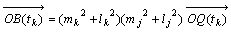
摨條偵
丂丂丂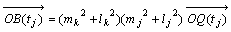
偲偍偔丅嘊傛傝忋偺儀僋僩儖傪惉暘偱昞偡丅 偺倶嵗昗丆倷嵗昗傪媮傔傞丅
偺倶嵗昗丆倷嵗昗傪媮傔傞丅
倶嵗昗偼
丂丂丂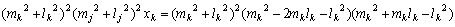
摨條偵倷嵗昗偼
丂丂丂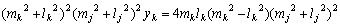
偙傟傛傝倶嵗昗丆倷嵗昗偲傕偵惍悢偱偁傞丅
摨條偵 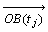 傕倶嵗昗丆倷嵗昗偲傕偵惍悢偱偁傞丅
傕倶嵗昗丆倷嵗昗偲傕偵惍悢偱偁傞丅
師偵丆俀揰俷俛(倲k)俷俛(倲j)偺嫍棧傪媮傔傞丅
丂丂丂仮俷俻(倲k)俻(倲j)佷仮俷俛(倲k)俛(倲j)
偱偁傝丆憡帡斾偼
丂丂丂(倣k2亄倢k2)2 (倣j2亄倢j2)2
傛傝
丂丂丂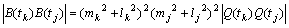
傛偭偰
丂丂丂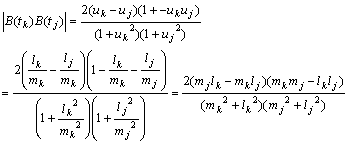
偙傟傪梡偄偰
丂丂丂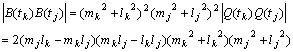
傛偭偰丆俛(倲k)丆俛(倲j)偺椉曽偲傕偵倶嵗昗丆倷嵗昗偑惍悢偲側傞丅傑偨俀揰娫偺嫍棧 俛(倲k)俛(倲j)傕惍悢偲側傞丅
偙傟傛傝俙1丆俙2丆俙3丆俙4丆俙5丆丒丒丒俙n 傪嶌傞丅
(倣k2亄倢k2)亖俵k偲偍偒丆俵亖俵1l2l3ゥゥ俵n偲偍偔丅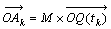 偲偍偔偲丆
偲偍偔偲丆
丂丂丂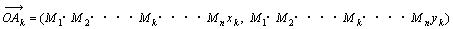
偲側傝惍悢偱昞偡偲
丂丂丂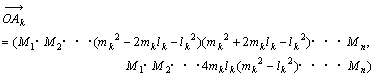
丂 (忋偺幃偱偼倠斣栚偺俵k偑側偔偰幃偑偦偺戙傢傝偵擖偭偰偄傞丅)
偙偺傛偆偵偟偰嶌偭偨値屄偺揰俙1丆俙2丆俙3丆ゥゥ俙n偼慡偰敿宎俵忋偺戞堦徾尷偵偁傞偐傜栤戣偺媮傔傞傕偺偵側偭偰偄傞丅
| 乽俽倎倰倓偺掕棟乿 倖傪俼n偺奐廤崌倂偐傜俼m傊偺俠亣幨憸偲偟俠傪倖偺椪奅揰慡懱偐傜側傞廤崌偲偡傞偲偒丆倖(俠)偼俼m偺應搙侽偺廤崌偱偁傞丅 |
| 乽椪奅揰偺掕媊乿 倖傪俼n偺奐廤崌倂偐傜俼m傊偺俠亣幨憸偲偡傞丅倂偺揰倶偵偍偗傞倖偺旝暘學悢倓倖(倶)偑倰倎値倠(倓倖(倶))亙倣傪枮偨偡偲偒丆x傪倖偺椪奅揰偲屇傇丅 |