魔方陣について

追分高等学校　長谷川貢

　私の学校は，学力差がかなり大きくて，小テストをかねてプリントを配っても，１０人くらいはほとんど手が着かない状態である。そのために，早く問題を解き終えた生徒のために４×４の魔方陣を与えてみた。

『図の□の中に１から１６までの数を入れて，縦・横・斜めの升の中にある数の合計が全て３４となるようにしなさい。』

　初めは次のような図を黒板にかいて，早く終わった生徒がどのくらいこの問題に関心があるかを見守ることにした。

　好奇心旺盛な女子が色々と数字を入れていたが１０分ぐらいではとても出来そうではなかった。仕方がないから，１列だけでもと数字を入れたが，まだ解けないので，全部で７個だけ数字を入れたところ，何人かが魔方陣を完成することが出来た。
授業の感想

　問題を見たとき，何となく出来そうな気がするのがこの手の問題の良いところであり，さらに正解が４８種類もあるところがとても魅力的なところと思う。つまり，正解を発表してもそれ以外の解答が腐るほどあるから，何度でもこのネタは使うことが出来るわけである。ひょっとしたら１年に１回の割で使えば定年になるまで，毎回違った解答を披露することが可能であるのだ。とても楽しいではないだろうか。
　ここに１つの解答を載せておきます。

　魔方陣を解くコツは次のものを見ればお分かりいただけると思います。

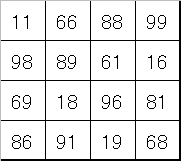
　下の魔方陣は，上下逆さまにしても成り立ちます。
　よかったら授業で試してみてください。

魔方陣のたねあかし

　４進法で１から１６までを表わしてみる。

　　00，01，02，03，10，11，12，13，20，21，22，23，30，31，32，33

となる。この１桁目と２桁目に注意をする。
　　１桁目は　０＋１＋２＋３＝１２
　　２桁目は　００＋１０＋２０＋３０＝１２０
となる。この両方をたして
　　１２＋１２０＝１３２
となり，この値が全部の平均の４倍となっている。よって０，１，２，３の４個からなる巡回群を考える。

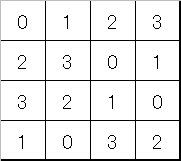ｆｉｇ１	ｆｉｇ２

　これは下に書いた表を１桁目と２桁目に分割したにすぎない。またよく見ていただければお分かりになるように，縦・横・斜めには同じ数字が入っていないことと，２つの表を重ねあわせたときに同じ組み合わせが１つもないように作ってある。よって縦・横・斜めのどこをたしても，全ての数が同じ回数だけあるから，合計も同じになると言うことである。
　１から３６までにすれば，正解が多すぎて何回でも使えることと思う。