１．始めに

　空間図形の扱いが困難なことの要因として考えられるものを上げてみることにする。第一には，黒板に図を描いても，それが立体的に見えないことが多いので，問題のもっている図形の位置が想像できない。第二には，座授をどのようにとればよいのかか分かりにくいことであろう。

　軌跡に関する問題もよくにている性質をもっている。ある条件を満たす平面上の点が，同一平面上を動き回るとき，その点の軌跡のもつ性質を理解できていないと，計算だけによってでてきた結果が正しいか間違っているかの判碗も難しくなる。

　以上のことから，まずは問題の意味を理解するために，いろいろなことを試みた訳である。

２．模型を用いたことによる効果について

　具体的に対象となる立体を手に持ってあらゆる角度からなかめると，その問題のもっている図形の性質が見えてくる。そして，そこから新しい手掛かりが見つかるわけである。

３．具体例

1. ペットボトルを用いた立体の交差に関する問題

   xyz空間において，x軸と平行な柱面 　　A:{(x，y，z)|y2+z2=1，x，y，zは実数} からy軸と平行な柱面 　　B={(x，y，z)|x2-√3xz+z2=1/4，x，y，zは実数} により囲まれる部分を切り抜いた残りの図形をCとする。図形Cの展開図を描け。 　ただし，点(0，1，0)を通りx軸と平行な直線に沿ってCを切り開くものとする。 (92東京大・理系)

   《作業》

   　ペットボトルを図のように切って，その中心に透明なプラスチック板を置く。その板にだ円を描く。次に，ベットポトルの回りの半分に上質紙を張る。板の正面から光を当ててその影が上質紙に写っているから，それをペンでなぞったものが求める展開図である。

   
   

2. 直方体の角を切り取った図形について

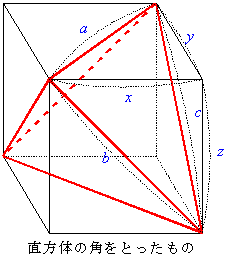
   3辺の長さかBC=2a，CA=2b，AB=2cであるような鋭角三角形ABCの3辺BC，CA，ABの中点をそれぞれL，M，Nとする。線分LM，MN，NLに沿って三角形を折り曲げ，四面体をつくる。 　その際，線分BLとCL，CMとAM，ANとBNはそれぞれ同一視されて，長さがa，b，cの辺になるものとする。 (1)線分MN，BLの中点をそれぞれP，Qとする。 　四面体を組み立てたとき，空間内の線分PQの長さを求めよ。 (2)この四面体の体積をa，b，cを用いて表せ。 (95東京大・理�T・後期)

   《模型の作成》

   　3辺がx，y，zの直方体から，4個の3角錐を切り取り残った4角錐を見ればすぐに理解出来る。つまり，合同な3角錐4個と4角錐1個を作ればよいのである。

   
   

3. 樹木の透き間から向こうの景色が見える。

   xy平面上，x座標，y座標がともに整数であるような点(m，n)を格子点とよぶ。各格子点を中心として半径rの円か描かれており，傾き2/5の任意の直線はこれらの円のどれかと共通点をもつという。このような性質をもつ実数rの最小値を求めよ。 (91東京大・理系)

   《模型の作成》

   　図のような丸い板にトイレットペーパーのしんを当間隔に立てて並べる。ちょうど傾きが2/5となるように眺めたとき，向こうの景色が見えなくなる最大の幅が求めるものである。ただしこの場合は，トイレットペーパーのしんの中心の距離と半径の比の値が答えとなる。

   
   

4. ローブにつないだ牛の行動範囲について

   xy平面内に2つの集合 　　l={(-5，y)l-5<y<5}，m={(5，y)|5<y<5)}を考える。 　l，m上にない2点A，Bに対しA，Bをl，mと交わらない線分または折れ線で結ぶときの経路の長さの最小値をd(A，B)で表す。　2点P(-9，-3)，Q(9，8)に対しd(P，R)=d(Q，R)となる点Rの軌跡をxy平面上に図示せよ。 (93東京大・理系)

   《模型の作成》

   　ダンポールに正方形の箱を置く。側面を切り取り，その中心を原点とする。P，Qが原点で対称であるからダンポールの裏側にミシンで使う糸巻きをつける。糸巻きから糸を出して2点P，Qから出す。糸巻きから同じ長さの所に鉛筆をつないで糸がたるまないように鉛筆を動かす。また，鉛筆と点Pの長さはいつも最短距離となるようにする。このようにして出来た鉛筆の跡が求める軌跡である。
   　つまり，鉛筆が牛の代わりになる訳である。

5. クラッカーの輪切り

   空間に直円錘Cがある。その頂点Pの座標は(0，0，-2)で，Cをxy平面で切った口は， 　　だ円：(x-1)2+(y2/a)=1(0<3<1) である。Cの母線の長さが4であるとき (1)Cの底面を含む平面の方程式を求めよ。 (2)aの値を，α√2+β(α，βは整数)の形で求めよ。 (93岐阜薬大)

   《模型の作成》

   　メがホンを斜めに置いてこれを幹切りにする。あとは，その切り口をよく見ればすぐに分かる。

6. 電球の下で読む本の陰の動き

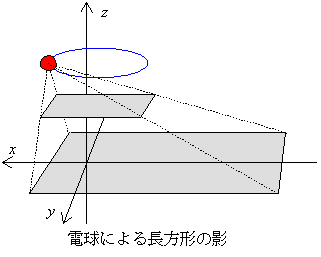
   a，b，cを実数とする。xyz空間において 　　|x|≦a，|y|≦b，z=c を濃たす点(x，y，z)からなる板Rを考える。点光源Pが平面Z=c+1上のだ円 　　(x2/a2)+(y2/b2)=c+1 の上を1周するとき，光が板Rにさえぎられてxy平面上にできる影の通過する部分の図を描き，その面積を求めよ。 (91東京大・理系)

   《模型の作成》

   　細長い捧を立てて，その中間に長方形の板をつける。さらにもう少し上に，針金でだ円を作りうまく棒に固定する。その針金に豆電球をつけてその影を見ればよく分かる。
   

<--