 《模型の作り方》
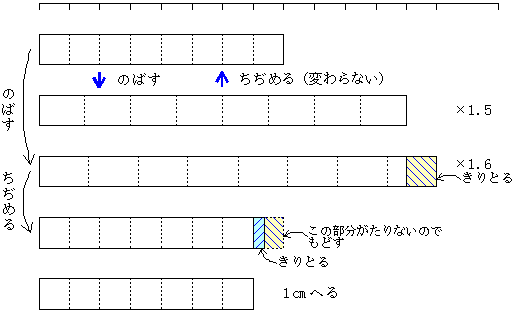
《模型の作り方》1.伸び縮みするゴムひも
| 間 実教xに対して,x以下の整数のうちで最大のものを[x]と書くことにする。 c>1として,an=[nc]/cとおく。以下(1)(2)(3)を証明せよ。 (1) すべてのnに対して,[an]はnまたはn-1に等しい。 (2) cが有理数のときは,[an]=nとなるnが存在する。 (3) cが無理数のときは,すべてのnに対して,[an]=n-1である。 (97北大・理系) |
 《模型の作り方》
《模型の作り方》
《考え方》
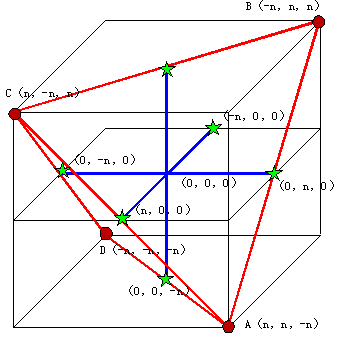
2.正四面体を表す平面の不等式について (正四面体の断面図について)
間 nを正の整数とする。連立不等式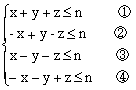 をみたすxyz空間の点P(x,y,z)でx,y,zがすべて整数であるものの個数をf(n)とおく。 極限 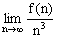 を求めよ。 を求めよ。(98東大・理科・前期) |
 《模型の作り方と考え方》
《模型の作り方と考え方》
3.ハートを回転させたときの体積(林檎の体積)
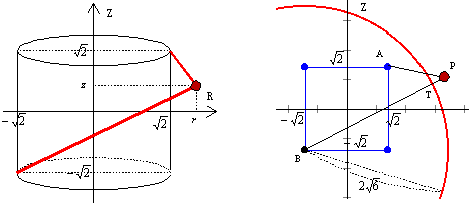
| 座標空間において, 平面z= 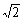 上にある半径 上にある半径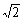 ,中心(0,0, ,中心(0,0,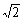 )の円をC1 )の円をC1平面z=- 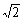 上にある半径 上にある半径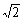 ,中心(0,0,- ,中心(0,0,-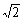 )の円をC2 )の円をC2とする。また,空間内の点P(x,y,z)に対し,円C1上を動く点QとPの距離の最小値をm,円C1上を動く点RとPの距離の最大値をMとする。次の間に答えよ。 (1)r= 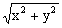 とおくとき,mとMをrとzで表せ。 とおくとき,mとMをrとzで表せ。(2)IM-2 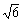 l≧mという条件を満たす点Pの範囲をHとする。図形Hの体積を求めよ。 l≧mという条件を満たす点Pの範囲をHとする。図形Hの体積を求めよ。(98大阪大・理系・前期) |
《模型》


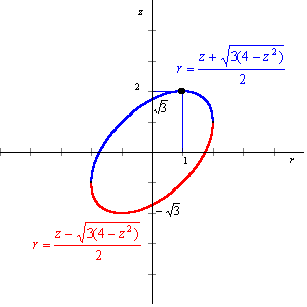
4.正八面体の投影図・側面図・展開図の描き方
(実物を見れば,なんてことはない,すぐに分かる。)
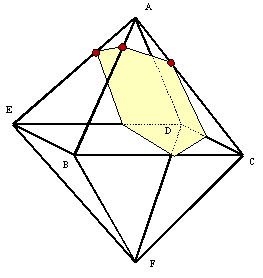
| 図のような1辺の長さが1の正八面体ABCDEFがある。AB,AC,AEをそれぞれ t:1-t,s:1-s,s:1-s (0<t<1,0<s<1) の比に内分する点をP,Q,Rとする。3点P,Q,Rを通る平面をαとしαはADに平行であるとする。 (1)t,sの満たす条件を求めよ。 (2)平面αによる正八面体の切り口はどのような図形か。またその断面穣をtで表せ。 (93浜松医大) |
《感想》

5.山の地形図を作る。(山の立体模型)
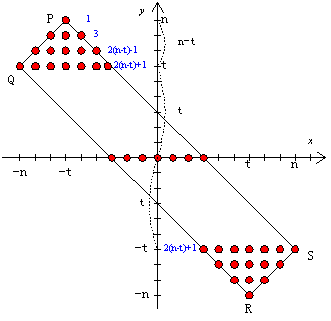
実数aに対してk≦a<k+1をみたす整数kを[a]で表す。nを正の整数として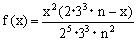 とおく。36n+1個の整数[f(0)][f(1)][f(2)]…[f(36n)]のうち相異なるものの個数をnを用いて表せ。 (98東京大学・理科) |
《模型》
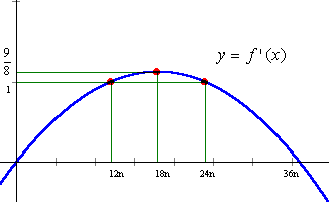
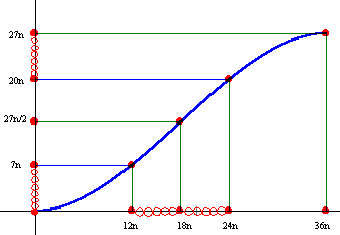
今年はおもいきって,パイプのジョイント部分を購入しました。
少しでも空間座標の概念が形成されればという思いからです。
まだー回しか使っていませんが,これから少しづつ使えるようにしていきたいと思っております。
◎ 今回の感想
nを充分に大きくしていくと,nのニ次以下の項はすべて零と見なすことができるのである。
「測度0の集合の加算個の和は測度0である。」という過去の記憶がよみがえってきた。
毎年,大学入学試験が行われ,その都度いろいろは問題が出題される。自分ではその問題がどのような観点から出題されたのかということが気になるので,いつも楽しみにしている。しかし,その中には,もうニ度と解きたくないと思われる問題がある。
私たち教師は,時間に制限があるわけではないし,解けないとしても,別に大学を受験している訳ではないから,しいていえば「生徒に聞かれたときに少し困る。」ということぐらいであろう。
私のモットー
「すべて受験の基本は教科書にある。」
どんなに難しい難問や奇問も,教科書に載っている内容を理解しておけば,すべて解くことができる。要は,教科書の内容を自分のものにできたか,ということである。
これからも教科書を大切にしていきたいと思っています。