丂丂丂亅1亝p(亅1)亖a亅b亄c亝1丆亅1亝p(0)亖c亝1丏亅1亝p(1)亖a亄b亄c亝1
偙偺忦審偐傜q(x)偺捀揰偺嵗昗傪兛偲偍偔偲丆兛亖亅b/2c傛傝
丂丂丂
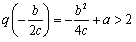
偐傜柕弬傪摫偒弌偦偆偲偟偨偑丆偆傑偔偄偒傑偣傫偱偟偨丅
傗偼傝丆偙偺栤戣偼恾宍偵棅傞偺偑堦斣偱偟傚偆丅
丂栤戣傪峫偊傞偲偒丆僌儔僼傪棙梡偡傞偲偐恾偵昤偄偰傒傞曽朄偼偲偰傕戝愗偱偡丅崱夞傕丆忦審偲偟偰梌偊傜傟偨傕偺傪丆悢幃傪曄宍偟偰夝偙偆偲偟偨偲偙傠丆僀儊乕僕偑晜偐偽側偔偰摨偠偲偙傠傪丂摪乆弰傝偟偰偄傑偟偨丅偲偙傠偑丆僌儔僼傪昤偄偨偲偙傠丆壗張偑暘偐傝偵偔偐偭偨偐傛偔暘偐傝傑偟丂偨丅偦偺揰偵偮偄偰傑偲傔傑偡丅
|
亂娫亃a丏b丆c偼幚悢偱 a亞0丆b亞0偲偡傞丅 丂丂丂p(x)亖ax2亄bx亄c丆丂q(x)亖cx2亄bx亄a 偲偍偔丅亅1亝x亝1傪傒偨偡偡傋偰偺x偵懳偟偰乥p(x)乥亝1偑惉傝棫偮偲偒 丂丂丂亅1亝x亝1 傪傒偨偡偡傌傋偰偺x偵懳偟偰乥q(x)乥亝2偑惉傝棫偮偙偲傪帵偣丅 (1995擭丆嫗搒戝妛丒棟宯妛晹丒屻婜擔掱)
|
丂偙偺栤戣偼忦審偑懡偡偓傞偨傔杮幙傪尒棊偲偟偰偟傑偆庴尡惗偑懡偐偭偨偲巚傢傟傑偡丅偙偙偱戝愗側偙偲偼丆
丂丂丂亅1亝f(1)亝1丏亅1亝f(0)亝1丆亅1亝f(亅1)亝1
傛傝
丂丂丂亅1亝a亄b亄c亝1丆亅1亝c亝1丏亅1亝a亅b亄c亝1
偲偄偆忦審偑嶌傜傟傑偡丅偨偭偨偙傟偩偗偱徹柧偑偱偒傑偡丅
q(x)亖cx2亄bx亄a傪旝暘偟偰q'(x)亖2cx亄b亖0偐傜幉偼x亖亅b/2c偙傟傪x1偲偍偔丅
乮鶣乯x1亝亅1傑偨偼x1亞1偺偲偒
q(x)偼亅1亝x亝1偱扨挷憹壛傑偨偼扨挷尭彮傛傝亅1亝x亝1傪傒偨偡偡傋偰偺x偵懳偟偰乥q(x)乥亝1偑惉傝棫偮偐傜亅1亝x亝1傪傒偨偡偡傋偰偺x偵懳偟偰乥q(x)乥亝2偑惉傝棫偮丅(恾傛傝柧傜偐)乮鶤乯亅1亙xl亙1偺偲偒
捀揰傪(x1丆y1)偲偍偔丅偙偺偲偒min{乥1亅x1乥,乥x1亅1乥}亝1傛傝丂偮傑傝丆忦審a亞0丏b亞0偼側偔偰傕椙偄偲尵偆偙偲偵側傝傑偡丅偟偐偟丆偙偺忦審傪堄幆偟偡偓偰丆夝偒曽傪娫堘偊偨恖偑偄偨偲巚偄傑偡丅
丂丂丂min{乥x1亅(a亄b亄c)乥,乥x1亅(a亅b亄c)乥}亝乥c乥亝1
傑偨丏max{乥a亄b亄c乥,乥a亅b亄c乥}亝1傛傝
丂丂丂max{乥c乥亄乥a亄b亄c乥,乥c乥亄乥a亅b亄c乥}亝2
傛偭偰亅1亝x亝1傪傒偨偡偡傋偰偺x偵懳偟偰乥q(x)乥亝2偑惉傝棫偮
巹偺姩堘偄偵偮偄偰
乥p(x)乥亝1丆a亞0丆b亞0傛傝
丂丂丂亅1亝p(亅1)亖a亅b亄c亝1丆亅1亝p(0)亖c亝1丏亅1亝p(1)亖a亄b亄c亝1
偙偺忦審偐傜q(x)偺捀揰偺嵗昗傪兛偲偍偔偲丆兛亖亅b/2c傛傝
丂丂丂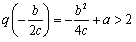
偐傜柕弬傪摫偒弌偦偆偲偟偨偑丆偆傑偔偄偒傑偣傫偱偟偨丅
傗偼傝丆偙偺栤戣偼恾宍偵棅傞偺偑堦斣偱偟傚偆丅