【演習】数式処理ソフト Mathmedia　

～数値計算・数式処理・グラフィックスの基礎実習～

@Author　Masasi.Sanae　　@Version　1.00;2002.7.10

　このレポートで使用されているMathmediaのデータファイルと，Mathmediaと同じコードで作成したMathematicaのデータファイルをダウンロードすることができます。
　　　Mathmediaのデータファイル　　「Mathmedia.log」（約7KB）
　　　Mathematicaのデータファイル　「Mathmedia.nb」（約47KB）

数式処理ソフト『Mathmedia』とは
　数式処理ソフト『Mathmedia』は，中学生・高校生から専門的な科学技術計算まで幅広いニーズに応える数学ソフトである。機能としては、数値計算・数式処理・グラフィックス／サウンドの３つの基本機能がある。
　数式処理ソフトといえばMathmaticaやMapleなどの優れたものがあるが，これらは価格も非常に高く一般の人がなかなか気軽に利用できるものではない。しかし数式処理ソフトを活用することで，より数学を深く理解することできることも事実である。Mathmediaはそうしたユーザーが気軽に利用できることを目指したシェアウエアソフトといえる。
　特にコマンド等はMathematicaとほとんど変わらず，Mathematicaの学習用として用いることもできる。今回の演習では全てMathematicaのコマンドと同じものを用いて実習する。グラフィックス機能などまだまだ不十分な点はあるが，数式処理の入門用として用いるには最適なソフトウエアだといえる。
　数式処理ソフト『Mathmedia』についての詳しいことは，下記のHPにあるので是非ダウンロードして試してみて頂きたい。
　　　http://www.gulf.or.jp/~damayan/math/index.html
数値計算
　まずは電卓機能としての使い方である。かけ算は*で，わり算は/で表す。かけ算は*の代わりにスペースでも可能である。
1. 足し算
  In[1]:=8.1+2.5
  Out[1]:=10.6
2. 引き算
  In[2]:=8.1-2.5
  Out[2]:=5.6
3. かけ算
  In[3]:=8.1*2.5
  Out[3]:=20.25
4. わり算
  In[4]:=8.1/2.5
  Out[4]:=3.24
5. べき乗
  In[5]:=2.5^2
  Out[5]:=6.25
　得られた結果を次の入力に利用するには%を用いる。また2つ前の結果を利用するには%%を，Out[4]の結果を利用するには%4を用いる。
1. 結果の引用
  In[6]:=%/2
  Out[6]:=3.125
  In[7]:=%4*2
  Out[7]:=6.48
　整数と分数では厳密値として扱われ，近似値と区別される。厳密値を近似値に変換する場合は，組み込み関数Nを用いる。NはN[式, n]で精度を指定することができる。
1. 厳密値と近似値
  In[8]:=305/177
  Out[8]:=305/177
  In[9]:=1/6+305/177
  Out[9]:=223/118
  In[10]:=N[%]
  Out[10]:=1.8898305084745763
  In[11]:=N[Sqrt[2],50]
  Out[11]:=1.4142135623730950488016887242096980785696718753769
数値関数
　mのnによる整商と余りを求めるには，それぞれQuotient，Modを用いる。
1. 余り，商
  In[1]:=Mod[17,3]
  Out[1]:=2
  In[2]:=Quotient[17, 3]
  Out[2]:=5
　近似値から厳密値への変換を行う組み込み関数はいくつかある。Roundは小数点第1位を四捨五入して整数を返す。ただし，ちょうど1.5では１となる。
　Floorは実数をそれを超えない最大の整数へと変換する。Ceilingは小数点以下を切り上げて得られる整数を返す。
1. 四捨五入，超えない最大の整数
  In[3]:=Round[2.3]
  Out[3]:=2
  In[4]:=Round[{1.0,1.2,1.4,1.5,1.6,1.8,2.0}]
  Out[4]:={1, 1, 1, 2, 2, 2, 2}
  In[5]:=Floor[{1.0,1.2,1.4,1.5,1.6,1.8,2.0}]
  Out[5]:={1, 1, 1, 1, 1, 1, 2}
　Absは実数または複素数zの絶対値を返します。zが複素数の時，ガウス平面における原点からの距離を返す。
1. 絶対値
  In[6]:=Abs[{-1.2,0,3.4}]
  Out[6]:={1.2, 0, 3.4}
  In[7]:=Abs[3.0+4.0I]
  Out[7]:=5.0
　リストの最大値・最小値を返すにはMax，Minを用いる。
1. 最大値・最小値
  In[8]:=Max[23,-32,45,98,17]
  Out[8]:=98
  In[9]:=Min[23,-32,45,98,17]
  Out[9]:=-32
　数値をn進数で表すにはBaseFormを用いる。n進数の表記は n^^XXX と表される。In[11]では1000000を16進数で表し，In[12]で10進数に戻している。
1. 記数法
  In[10]:=BaseForm[100,2]
  Out[10]:=2^^1100100
  In[11]:=BaseForm[1000000,16]
  Out[11]:=16^^f4240
  In[12]:=16^^f4240
  Out[12]:=1000000
整数関数
　Divisors[n]は整数のすべての約数を，小さい順のリストにして返す。
1. 約数
  In[1]:=Divisors[100]
  Out[1]:={1, 2, 4, 5, 10, 20, 25, 50, 100}
　整数の最大公約数，最小公倍数を求めるにはGCD，LCMを用いる。
1. 最大公約数・最小公倍数
  In[2]:=GCD[24,15]
  Out[2]:=3
  In[3]:=GCD[20,50,120]
  Out[3]:=10
  In[4]:=LCM[24,15]
  Out[4]:=120
　FactorInteger[n]は整数nを素因数分解し，結果は素因数と指数のリストを要素に持つリストを返す。Out[5]は2^3*3*5を表している。
　結果を直感的な表示（再入力可能な式）で返す場合はIFactorを用いる。（注：MathematicaにはIFactorはない。）
1. 素因数分解
  In[5]:=FactorInteger[120]
  Out[5]:={{2, 3}, {3, 1}, {5, 1}}
  In[6]:=IFactor[120]
  Out[6]:=2^3 * 3 * 5
　n番目の素数を求めるにはPrime[n]を用いる。Prime[1] は2である。In[8]ではTableを用いて1番目から10番目の素数を求めている。
　PrimePi[n]でn以下の素数の個数を求めることができる。
1. 素数（n番目の素数，素数の個数）
  In[7]:=Prime[10]
  Out[7]:=29
  In[8]:=Table[Prime[i],{i,1,10}]
  Out[8]:={2, 3, 5, 7, 11, 13, 17, 19, 23, 29}
  In[9]:=PrimePi[30]
  Out[9]:=10
　PowerMod[a, b, n]は法計算でのベキ乗 a^b mod n を返す。n>0でなければならない。Mod[a^b,n]としても同じ結果を与えるが，PowerMod の方が効率よく計算できる。
　bが負の場合，k*a^(-b) mod n = 1 となるkを返します。特に b=-1 の場合，法計算でのの逆元を表す。
1. 法計算でのべき乗，逆元
  In[10]:=PowerMod[2, 3, 7]
  Out[10]:=1
  In[11]:=PowerMod[3, -1, 7]
  Out[11]:=5
初等関数
　組み込み関数を用いると，様々な初等関数を求めることができる。組み込み関数は，一般に　関数名[．．．]という形をしている。関数名は大文字から始まる英文字のれつで，ほとんどの場合フルネームで書かれる（Sqrtなどは例外）。
　平方根を求めるにはsqrtを用いる。基本的には厳密値で表されるが，小数値を指定したりNを用いると近似値を得ることができる。Sqrtの因数としては複素数を指定することもできる。
1. ルート
  In[1]:=Sqrt[2]
  Out[1]:=Sqrt[2]
  In[2]:=Sqrt[2.0]
  Out[2]:=1.4142135623730951
  In[3]:=N[Sqrt[2]]
  Out[3]:=1.4142135623730951
  In[4]:=Sqrt[2.0+3.0I]
  Out[4]:=1.6741492280355401 + 0.8959774761298381 I
　三角関数を求める場合，引数の単位はラジアンです。度にするには Degree をつける。
1. 三角関数
  In[5]:=Sin[Pi/6]
  Out[5]:=1/2
  In[6]:=Sin[30 Degree]
  Out[6]:=1/2
  In[7]:=N[Sin[1], 30]
  Out[7]:=0.84147098480789650665250232163
　a を底とする対数はLog[a, x] を用いる。aを省略したLog[x]は自然対数を返す。これはLn[x]と同値である。
1. 指数・対数
  In[8]:=Log[1/4, 8]
  Out[8]:=-3/2
  In[9]:=Log[2, 10]
  Out[9]:=Log[2, 10]
  In[10]:=Log[2.0, 10.0]
  Out[10]:=3.3219280948873626
  In[11]:=N[Log[2, 10], 30]
  Out[11]:=3.32192809488736234787031942921
  In[12]:=Exp[1.0]
  Out[12]:=2.718281828459045
　代表的な定数値としてπやｅなどの組み込み定数は厳密値を持つ。
1. 組み込み定数
  In[13]:=N[Pi]
  Out[13]:=3.141592653589793
  In[14]:=N[E, 30]
  Out[14]:=2.71828182845904523536028747135
代数計算
　シンボル計算（または文字式の計算）の足し算，引き算は，同類項をまとめる計算である。シンボルはスペースを含まない英数字の列で，何文字でよい。たとえばsikiもyzもそれぞれ1つのシンボルである。y zのようにスペースを入れるとy*zを表す。
　先頭は数字でなくてはいけない。数字に文字が続くと，スペースがなくてもかけ算の意味となる。たとえばx2は一つのシンボルだが，2xはxの2倍を表す。
1. シンボル計算
  In[1]:=(3x-4y)+(2x-5y)
  Out[1]:=5 x - 9 y
  In[2]:=(2x)^2+(x2)^2+(yz)^2+(y z)^2
  Out[2]:=4 x^2 + x2^2 + yz^2 + y^2 z^2
　展開をするにはExpandを用いる。Mathmediaには，微分，積分をはじめ，シンボル計算（数式処理）を行う様々な組み込み関数がある。
　シンボルには値を割り当てることができる。例えば次の式ではa+2bをシンボルxに割り当てている。言い換えると，式a+2bにzと名をつけることと同じである。関連づけられた定義をすべて消去するにはClearを用いる。
1. 展開
  In[3]:=Expand[(x+2)^2]
  Out[3]:=4 + 4 x + x^2
  In[4]:=x=a+2b
  Out[4]:=x + 2 b
  In[5]:=Expand[x^3]
  Out[5]:=a^3 + 6 a^2 b + 12 a b^2 + 8 b^3 In[6]:=Clear[x] Out[6]:=Null
　因数分解をするにはFactorを用いる。
1. 因数分解
  In[7]:=Factor[x^4+x^2+1]
  Out[7] := (1 - x + x^2) (1 + x + x^2)
  In[8]:=Factor[x^10-1]
  Out[8]:=(-1 + x) (1 + x) (1 - x + x^2 - x^3 + x^4) (1 + x + x^2 + x^3 + x^4)
　分母の多項式が因数分解できるとき，この分数式はApartを用いて部分分数に分解できる。逆に共通分母に揃えて項をまとめるにはTogetherを用いる。
1. 部分分数分解，分母の共通化
  In[9]:=Apart[1/(x^2-1)]
  Out[9]:=-1/2/(1 + x) + 1/2/(-1 + x)
  In[10]:=Together[-1/2/(1 + x) + 1/2/(-1 + x)]
  Out[10]:=1/(-1 + x^2)
　代数方程式の解を求めるにはSolveを用いる。Solveの第1因数において，==は方程式における等号を表す。=はシンボルに値を割り当てるときにのみ使われる。
　結果における左辺->はルールといわれ，矢印の左辺を右辺に置き換える規則を表す。/.はルールを式に当てはめるコマンドで，例えば次のIn[11]ではx /. %を用いて解を取り出すことができる。
　Solveは厳密解を求める関数で，解の公式を用いた形で与えられる。
　1次の連立方程式を解く場合は，方程式と未知数のリストを指定する。
　方程式の近似解を求める場合はNSolveを用いる。
1. 代数方程式の解
  In[11]:=Solve[x^3 - 19*x + 30 == 0, x]
  Out[11]:={{x -> 3}, {x -> 2}, {x -> -5}}
  In[12]:=x /. %
  Out[12]:={3, 2, -5}
  In[13]:=Solve[x^3-8==0,x]
  Out[13]:={{x -> 2}, {x -> -1 - I Sqrt[3]}, {x -> -1 + I Sqrt[3]}}
  In[14]:=Solve[{x+y==1,2 x-7 y==11},{x,y}]
  Out[14]:={{x -> 2, y -> -1}}
  In[15]:=NSolve[x^2 -3 x-1==0,x]
  Out[15]:={{x -> 3.302775637731995}, {x -> -0.3027756377319946}}
　線形の方程式でなくても，方程式によっては解が求められるものもある。
1. 非線形方程式の数値解
  In[16]:=FindRoot[x/5==Cos[x], {x, 2}]
  Out[16]:={x -> 1.306440008369511}
微積分
　関数f(x)の導関数f'(x)は組み込み関数Dを用いて求める。
　3階の導関数f'''を求めるには，変数と回数をリストにする。
　D[ f[x, y], x ] は偏微分を表す。
1. 微分
  In[1]:=D[x^n,x]
  Out[1]:=n x^(-1 + n)
  In[2]:=D[x^2 Sin[x],{x,3}]
  Out[2]:=6 Cos[x] - 6 x Sin[x] - x^2 Cos[x]
  In[3]:=D[x y Sin[x Sin[y]],x]
  Out[3]:=y (x Cos[x Sin[y]] Sin[y] + Sin[x Sin[y]])
　不定積分を求めるにはIntegrateを用いる。
　定積分はIntegrateの第2因数をリストとして積分範囲を指定する。
1. 積分
  In[4]:=Integrate[x^n,x]
  Out[4]:=1/(1 + n) x^(1 + n)
  In[5]:=Integrate[Sin[x],{x,0,Pi}]
  Out[5]:=2
　数値積分を求めるときはNIntegrateを用いる。
1. 数値積分
  In[6]:=NIntegrate[x^2, {x, 0, 1}]
  Out[6]:=0.33333333333333337
  In[7]:=NIntegrate[Sqrt[1-x^2], {x, 0, 1}]
  Out[7]:=0.7853981633974477
　極限値を求めるにはLimitを用いる。
1. 極限
  In[8]:=Limit[(x^2-1)/(x^3-1),x->1]
  Out[8]:=2/3
  In[9]:=Limit[Log[x],x->0]
  Out[9]:=-Infinity
　関数Sin[x]/(x^2+4)をx=0の周りでテイラー展開し，8次の項まで求めてみよう。そのためにはSeriesを用いる。
　O[x]^9は剰余項がたかだかx⁹のオーダーであることを表す。したがって，この場合x⁸の項がないことがわかる。剰余項を取り除くにはNormalを用いる。
1. テイラー展開
  In[10]:=Series[Sin[x]/(x^2+4),{x,0,8}]
  Out[10]:=1/4 x - 5/48 x^3 + 9/320 x^5 - 571/80640 x^7 + O[x]^9
  In[11]:=Normal[%]
  Out[11]:=1/4 x - 5/48 x^3 + 9/320 x^5 - 571/80640 x^7
グラフィックス
　1変数関数f(x)のグラフは組み込み関数Plotを用いて描くことができる。
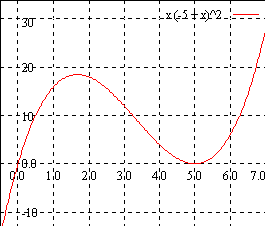
　次のIn[1]の例は，f(x)=x (x-5)²をxが-1から7までの範囲で描画している。
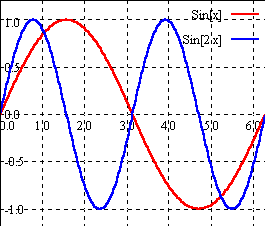
　In[2]では複数のグラフをリストにして描画している。
1. ２次元グラフ
  In[1]:=Plot[x (x-5)^2,{x,-1,7}]
  
  In[2]:=gr=Plot[{Sin[t],Sin[2t]},{t,0,2Pi}]
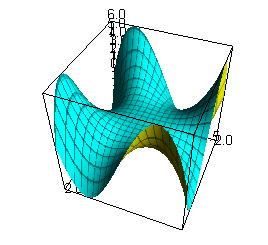
　2変数関数f(x, y)のグラフはPlot3Dによって描くことができる。高さ方向にz軸がとられてz=f(x, y)の表す曲面が描かれる。変数と範囲は2つのリストによって指定する。
1. ３次元グラフ
  Plot3D[ x y (x^2-y^2) , { x , -2 , 2 } , { y , -2 , 2 }]
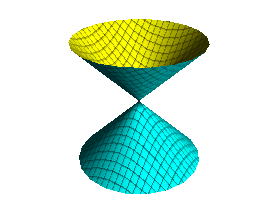
　2変数t,uの関数f(t, u)，g(t,u)，h(t,u)によってx=f(t,u)，y=g(t,u)，z=h(t,u)と表される曲面（パラメータ表示の曲面）はParametricPlot3Dを用いて描くことができる。3つの関数を{　}で囲んだリストを第1因数とする。
1. 媒介変数３次元グラフ
  ParametricPlot3D [ { u Cos [t] , u Sin [t] , u } , { t , 0.5 Pi , 2.5 Pi } , { u ,-Pi , Pi} ]
リスト/集合
　いくつかの数やシンボルをコンマで区切り，かっこ{　}で囲んだ全体をリストという。例えばIn[1]では整数とシンボルからなるリストにmojiという名をつけている。
　含まれている要素（リストを集合とすれば，元）の個数を，リストの長さという。リストの長さはLengthによって知ることができる。
　リストの要素を表すには，リストに続いて要素の番号を2重の角括弧[[　]]で囲む。例えばIn[3]ではmojiの表すリストの2番目の要素を取り出している。Firstを用いると先頭の要素を，Lastで最後の要素を取り出すことができる。
1. リスト
  In[1]:=moji={1,c,f,3,a,b}
  Out[1]:={1, c, f, 3, a, b}
  In[2]:=Length[moji]
  Out[2]:=6
  In[3]:=moji[[2]]
  Out[3]:=c
  In[4]:=First[moji]
  Out[4]:=1
　Range[n]は1からnまでの整数のリストを返すが，Range[m,n]とすると初期値がmとなる。また第3因数ででステップを指定することができる。
　In[7]，In[8]を見ていただきたい。このように，ほとんどの代数演算や組み込み関数はリストの個々の要素に作用する（リスタブル）。
1. 数値リストの生成
  In[5]:=Range[10]
  Out[5]:={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
  In[6]:=Range[10,2,-2]
  Out[6]:={10, 8, 6, 4, 2}
  In[7]:=z^Range[5]
  Out[7]:={z, z^2, z^3, z^4, z^5}
  In[8]:=Prime[Range[5]]
  Out[8]:={2, 3, 5, 7, 11}
　Rangeよりも少し込み入った数列はTableを用いて作る。In[9]の第2因数{n,6}は反復子と呼ばれ，nを1から6まで変えて第1因数が作り出す値のリストを作る。In[10]の反復子{n,2,6,2}は初期値が2，ステップ（刻み）が2であることを表している。反復変数がいらないときは{6}でもよい。
　反復子を複数指定すれば，リストのリストが作られる。In[11]ではインデックスjが1から4まで動いてサブリストが作られる。
1. テーブル
  In[9]:=Table[n (n+1),{n,6}]
  Out[9]:={2, 6, 12, 20, 30, 42}
  In[10]:=Table[n (n+1),{n,2,6,2}]
  Out[10]:={6, 20, 42}
  In[11]:=Table [ i - j , { i , 3 }, { j, 4} ]
  Out[11]:={{0, -1, -2, -3}, {1, 0, -1, -2}, {2, 1, 0, -1}}
　リストのすべての順列を生成するにはPermutationsを用いる。重複する順列は取り除かれる。個数を調べるにはLengthを用いる。
　リストの中からn個を選ぶ組み合わせを生成するにはCombinationsを用いる。（注：MathematicaにはCombinationsはない。）
1. 順列・組合せ
  In[12]:=Permutations[{a,b,c}]
  Out[12]:={{a, b, c}, {b, a, c}, {c, a, b}, {a, c, b}, {b, c, a}, {c, b, a}}
  In[13]:=Length[%]
  Out[13]:=6
  In[14]:=Permutations[{a,a,b,c}]
  Out[14]:={{a, a, b, c}, {b, a, a, c}, {a, b, a, c}, {b, a, c, a}, {a, b, c, a}, {c, b, a, a}, {b, c, a, a}, {a, c, b, a}, {c, a, b, a}, {a, a, c, b}, {c, a, a, b}, {a, c, a, b}}
  In[15]:=Combinations[{a, b, c, d, e}, 3]
  Out[15]:={{a, b, c}, {a, b, d}, {a, c, d}, {b, c, d}, {a, b, e}, {a, c, e}, {b, c, e}, {a, d, e}, {b, d, e}, {c, d, e}}
　2つの集合の積集合，和集合はそれぞれIntersection，Unionで表される。また補集合はComplementで表される。
1. 集合
  In[16]:=U=Range[1,10]
  Out[16]:={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
  In[17]:=X={1,2,4,5,7}
  Out[17]:={1, 2, 4, 5, 7}
  In[18]:=Y={2,3,4,8}
  Out[18]:={2, 3, 4, 8}
  In[19]:=Z={4,5,7,9}
  Out[19]:={4, 5, 7, 9}
  In[20]:=Intersection[X,Y]
  Out[20]:={2, 4}
  In[21]:=Union[X,Z]
  Out[21]:={1, 2, 4, 5, 7, 9}
  In[22]:=Complement[U,Y]
  Out[22]:={1, 5, 6, 7, 9, 10}
  In[23]:=Union[Intersection[X,Y],Complement[U,Z]]
  Out[23]:={1, 2, 3, 4, 6, 8, 10}
プログラミング
　整数の2乗のリスト{1,4,9,16}はTable[i^2,{i,4}]で作ることができる。TableをDoに変えると，式i^2をiを1から4まで繰り返すループができる。ただしDoは繰り返すだけで結果を返さない。これを使っても上の結果を得ることができるが，それには式をPrintに入れて表示させる。
　もっと古典的にはIn[2]のように，Forを使って初期値を決め，ループの終わりの条件を与え，インデックスを増やしながらPrint[i^2]を実行する。これは伝統的な手続き型プログラミングの方法であるが，ほとんど必要としない。
1. ループ
  In[1]:=Do[Print[i^2],{i,4}]
  1
  4
  9
  16
  Out[1]:=Null
  In[2]:=For[i=1,i<=4,i=i+1,Print[i^2]]
  1
  4
  9
  16
  Out[2]:=Null
　In[3]のようなパターンを使って関数を定義することができる。:=は遅延割り当てと呼ばれ，この式が入力されても右辺は評価されず，fの引数にxと名をつけ，右辺の式のルールが適用される。この関数が使われると，右辺が評価されてその結果が返される。
　In[5]は関数の結果を引数として関数の値を求めたものである。このように関数を入れ子とすることをfのネストという。関数のネストは高次関数Nestを用いて実行できる。3重リストはIn[6]のようにNest[f,1,3]とすればよい。
　ネストを複数回行った結果を得るにはNestListを用いる。In[7]は5回行った結果を返している。これを数値的に行うためには初期値を近似値1.0とすればよい。
1. ネスト
  In[3]:=f[x_]:=x/2+1/x
  Out[3]:=f[x_] := x/2 + 1/x
  In[4]:=f[1]
  Out[4]:=3/2
  In[5]:=f[f[1]]
  Out[5]:=17/12
  In[6]:=Nest[f,1,3]
  Out[6]:=577/408
  In[7]:=NestList[f,1,5]
  Out[7]:={1, 3/2, 17/12, 577/408, 665857/470832, 886731088897/627013566048}
  In[8]:=NestList[f,1.0,5]
  Out[8]:={1.0, 1.5, 1.4166666666666665, 1.4142156862745097, 1.4142135623746899, 1.414213562373095}
演習問題
1. 次の計算をせよ。また，厳密値のときはその近似値も求めよ。
  (1) 3×(2.95-1.69)+2.3
  Out[1]:=6.08
  (2)
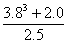
  Out[2]:=22.7488
  (3)
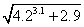
  Out[3]:=9.403244432896466
  (4)
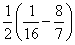
  Out[4]:=-121/224
  Out[5]:=-0.5401785714285714
  (5)
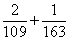
  Out[6]:=435/17767
  Out[7]:=0.024483593178364384
2. 次の問に答えよ。
  (1) 式(x+y+1/2)⁵を展開せよ。
  Out[8]:=1/32 + 5/16 x + 5/4 x^2 + 5/2 x^3 + 5/2 x^4 + x^5 + 5/16 y + 5/2 x y + 15/2 x^2 y + 10 x^3 y + 5 x^4 y + 5/4 y^2 + 15/2 x y^2 + 15 x^2 y^2 + 10 x^3 y^2 + 5/2 y^3 + 10 x y^3 + 10 x^2 y^3 + 5/2 y^4 + 5 x y^4 + y^5
  (2) 式x⁴+1024を因数分解せよ。
  Out[9]:=(32 - 8 x + x^2) (32 + 8 x + x^2)
  (3) x³⁰-8を因数分解せよ。
  Out[10]:=(-2 + x^10) (4 + 2 x^10 + x^20)
3. 次の問に答えよ。
  (1) 方程式 x⁴-2x³-x+2=0 をSolveとNSolveを用いて解け。
  Out[11]:={{x -> 2}, {x -> 1}, {x -> 1/2 (-1 - I Sqrt[3])}, {x -> 1/2 (-1 + I Sqrt[3])}}
  Out[12]:={{x -> 2.0}, {x -> -0.5 + 0.8660254037844387 I}, {x -> -0.49999999999999994 - 0.8660254037844386 I}, {x -> 0.9999999999999999}}
  (2) 連立方程式 x+2y+3z=4，-x+2y+2z=2，3x+2y-2z=-1 を解け。
  Out[13]:={{x -> 5/12, y -> 1/24, z -> 7/6}}
4. 次の問に答えよ。
  (1) 関数 y=e^-x2 sin nx の導関数を求めよ。
  Out[14]:=-2 x Exp^(-x^2) Log[Exp] Sin[nx]
  (2) 関数 y=sin(x² cos x) の導関数を求めよ。
  Out[15]:=(-x^2 Sin[x] + 2 x Cos[x]) Cos[x^2 Cos[x]]
  (3) 関数 y=x⁵ sin x の不定積分を計算せよ。
  Out[16]:=120 Sin[x] - 120 x Cos[x] - 60 x^2 Sin[x] - x^5 Cos[x] + 5 x^4 Sin[x] + 20 x^3 Cos[x]
  (4) 定積分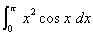を計算せよ。
  Out[17]:=-2 Pi
5. x^xのx→0における極限値を求めよ。また，x log x のx→0における極限値を求めよ。これらの関係を述べよ。
  Out[18]:=1
  Out[19]:=0
6. 次の関数のグラフを描け。
  (1) y=sinπx，y=sinπx/πx　（-5≦x≦5）
  Out[20]:=-Graphics-
  
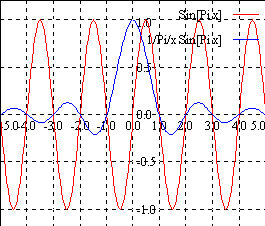
  (2) y=x+cos(2πx)　(0≦x≦24)
  Out[21]:=-Graphics-
  
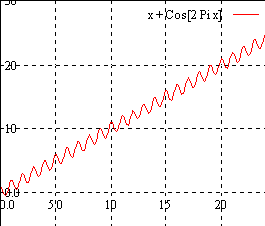
  (3) f(x,y)=(x²+3y²) e^1-x2-y2　(-3≦x≦3，-3≦y≦3)
  Out[22]:=-Graphics-
  
  (4) x=(2 + 0.5 cos u ) cos v，y= ( 2 + 0.5 cos u ) sin v)，z= 0.5 sin u + v/5　(0≦u≦2π，-3π≦v≦3π)
  Out[23]:=-Graphics-
7. 次の問に答えよ。
  (1) Table[n (n+1), {n, 6}] で得られるリストをRange[6]とリスタブルを使って作れ。
  Out[24]:={1, 2, 3, 4, 5, 6}
  Out[25]:={2, 6, 12, 20, 30, 42}
  (2) 数列{12, 16, 20, 24, 28}をTableを使って作れ。同じ数列をRangeを使って作れ。
  Out[26]:={12, 16, 20, 24, 28}
  Out[27]:={12, 16, 20, 24, 28}