(ａ+ｂ)ⁿを計算して展開式に現れる各項の係数を並べると、次の図のような配列が得られます。この数の配列をパスカルの三角形と言います。

　パスカルの三角形を調べると、いろいろな数列が現れます。例えば左から2番目の数を小さい方から順位に並べた数列
　　　1，2，3，4，5，6，･･･
は自然数の数列です。また、左から3番目の数を並べた数列
　　　1，3，6，10，15，21，･･･
は三角数、左から4番目の数を並べた数列
　　　1，4，10，20，35，･･･
は四面体数と呼ばれる自然数の数列です。

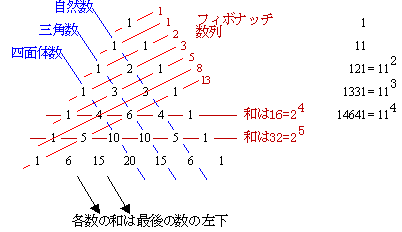
　また、上の図の赤い線の上に並ぶ数の和を求めてみましょう。このとき、得られた和を順に並べてできる数列
　　　1，1，2，3，5，8，･･･
はフィボナッチ数列と呼ばれ、隣接2項の和が次の項の数になっています。
　さらに、ｎ行目に並ぶ数の和を求めて得られる数列
　　　1，2，4，8，16，32，･･･
は　第ｎ項が　2^n-1　で与えられます。

　各数を横に見てみましょう。
　　　1，11,121,1331，…
この数列は第ｎ項が　11^n-1　で与えられます。
　各数を今度は斜めに見てみます。例えば右下がりの3列目の数列（三角数の数列でしたね），
　　　1，3，6，10，15，21，･･･
これの和を考えます。ｎ番目までの和をＳ_nとすると，
　　　Ｓ₂=1+3=4
　　　Ｓ₃=1+3+6=10
　　　Ｓ₄=1+3+6+10=20
出てきた数は最後の数の左下にある数になっています。