一定の条件を満たす軌跡の問題の中で、よく見落としがちな次のような問題を視覚的にとらえてみることを考えてみましょう。
| 点(x,y)が原点を中心とした半径1の円の周上及び内部を動くとき,点(x+y,xy)の動く領域を図示せよ。 |
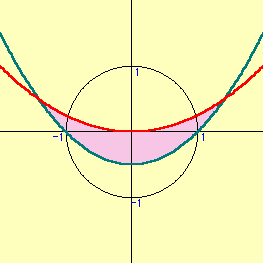 (解)x+y=u,xy=vとおくと,x2+y2≦1よりu2-2v≦1・・・①
(解)x+y=u,xy=vとおくと,x2+y2≦1よりu2-2v≦1・・・①
t2-ut+v=0の解よりD=u2-4v≧0・・・②
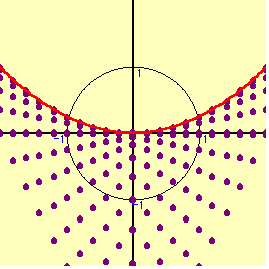
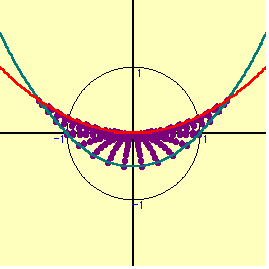
①,②より求める領域は右図のようになる。
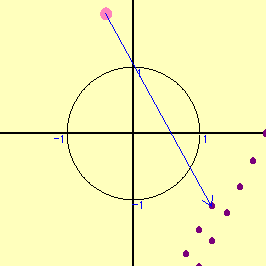
x2+y2≦1よりu2-2v≦1という式はすぐに導かれるが,実数条件を導くことを忘れてしまいがちな生徒が多いのではないだろうか。まず,具体的に円周上の点を動かしながら,点(x+y,xy)をプロットしていくことでイメ-ジを膨らませてみよう。
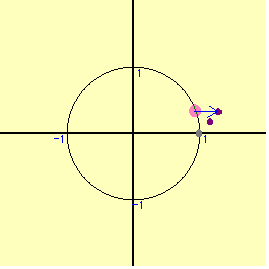
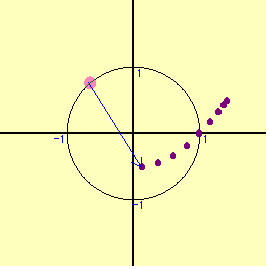
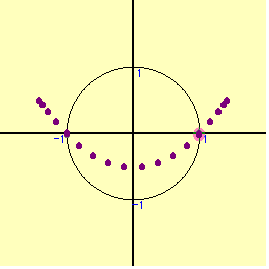
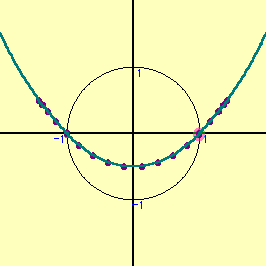
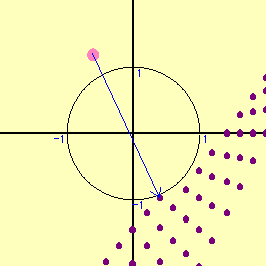
円周上を1周しても放物線の1部しか表れてこない。普通は周上の点をとると,ある程度の領域が表れるものであるが,全く姿を表さない。では,内部を動かそう。どのように動かしたら良いであろうか。むやみやたらに動かしても,うまく行かない。円の場合はx2+y2=r2 の半径rを変えて動かすことにより,円の内部の点を充足できる。半径を1から0.1づつずらして,連続的に中の点を動かしてみる。だんだん姿を表してきた。
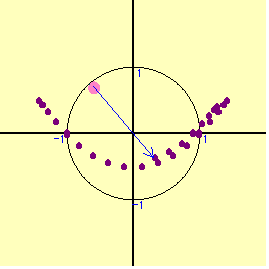
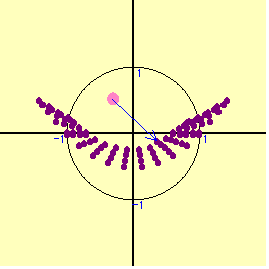
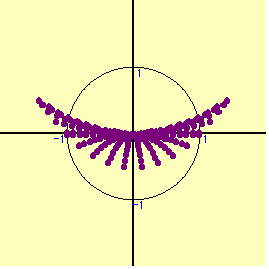
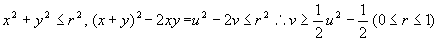 となり,1つの領域しか得られないが,コンピュ-タの表す図形はもう1つある。その実態は何か。
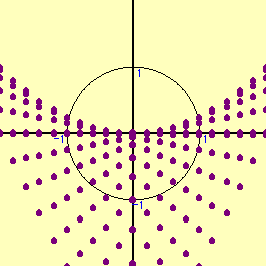
となり,1つの領域しか得られないが,コンピュ-タの表す図形はもう1つある。その実態は何か。実は,点(x+y,xy)のとりうる領域は,「円の周上及び内部」に関係なく,ある一定の図形を描くのである。実際に平面全体を一定の間隔で(x+y,xy)の点へ全て動かしてみよう。”実数x,y”という条件だけで,既に点(x+y,xy)はある領域を表しているのである。先ほどの円を動かした領域と,この点(x+y,xy)の表す領域で求める解が得られる。