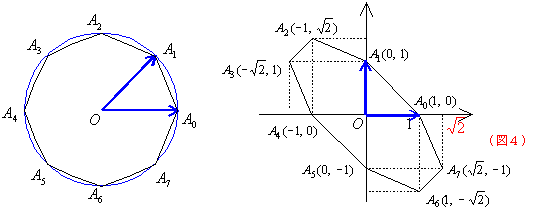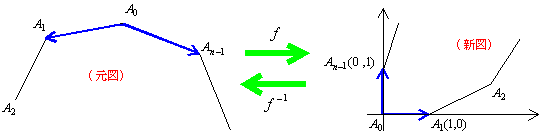
正n角形の図形に関連したベクトルの問題を効果的に解く方法について考えてみよう。正n角形の幾何的性質を明確に把みづらいのが原因でベクトルについての思考も滞ってしまう場合がよくある。そこで正n角形の図をデフォルメし,各頂点がなるべく簡単な座標で表わされるようなn角形を考える。すると座標を利用したベクトルの操作によって理論的な見通しが得られ易くなるのである。この場合,図は正n角形でなくなってしまうのは当然のことではあるが,【1】における1次変換の重要性質をふまえたものでなければならないのである。(元図)が正n角形であるとき(新図)はどのような図形であればよいか。

正n角形A0A1A2・・・An−1に対して,![]() =(a1,a2) ,
=(a1,a2) ,![]() =(b1,b2) を基底とするとき,fによって(新図)では
=(b1,b2) を基底とするとき,fによって(新図)では ![]() =(1,0),
=(1,0),![]() =(0,1) となるようにしたい。
=(0,1) となるようにしたい。
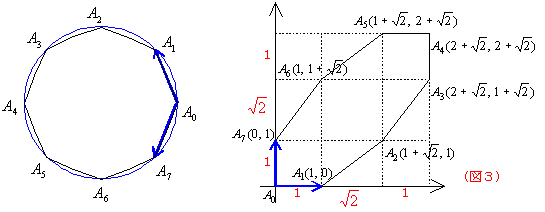
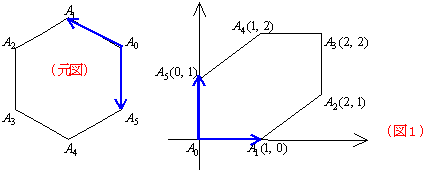
そしてこの場合,残りの頂点A2,A3,・・・,An−2 はどのような点になるのか。また(新図)はどのようなn角形になるのか。具体的にまず正6角形から考えてみよう。(元図)は正6角形A0A1A2A3A4A5で基底は![]() ,
,![]() とする。このとき(新図)は(図1)である。
とする。このとき(新図)は(図1)である。
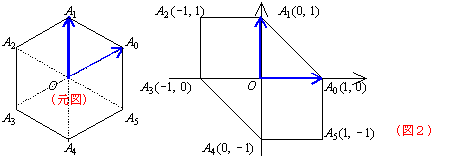
(元図)が正6角形A0A1A2 A3A4A5でも基底が![]() ,
,![]() のときは(新図)は(図2)のようになる。
のときは(新図)は(図2)のようになる。
これらの(図1)(図2)は1次変換の重要性質をすべて満たしていて,個々の点の座標も簡単な整数である。
ここで実際に問題を解いてみよう。
|
(例3)正6角形ABCDEFにおいて,CDを1:2の比に内分する点をGとする。
(1)
また,
(2) tを実数とする。
t =( ),
また, |
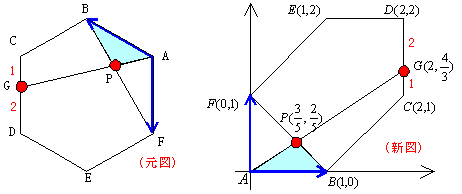
まず(元図)に基づいて(新図)を書いてみよう。
(新図)をもとに解答してみよう。
(1) ![]() =(2,2)=2(1,0)+2(0,1)=2
=(2,2)=2(1,0)+2(0,1)=2![]() +2
+2![]()
![]() =(2,1)=2(1,0)+(0,1)=2
=(2,1)=2(1,0)+(0,1)=2![]() +
+![]()
![]() =(2,
=(2,![]() )=2(1,0)+
)=2(1,0)+![]() (0,1)=2
(0,1)=2![]() +
+![]()
![]()
(2) ![]() =(1−t,t)
=(1−t,t)
よって点Pの座標は(1−t,t)。直線AGの方程式は![]() 。
。
この直線上に点Pがあるから,t=![]() (1−t) ∴t=
(1−t) ∴t=![]()
よってP(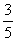 ,
,![]() ) 従って
) 従って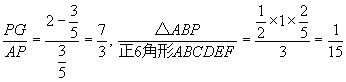
以上すべて(新図)より求めたものであるが,これらは(元図)においても成り立っているのである。
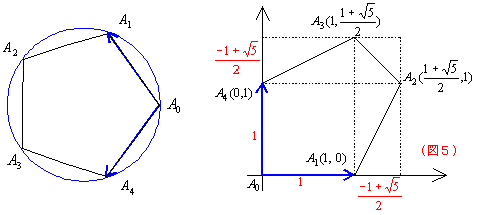
次に正8角形,正5角形について(元図)と(新図)を並べて書いておこう。正8角形では基底を![]() ,
,![]() にするか,
にするか,![]() ,
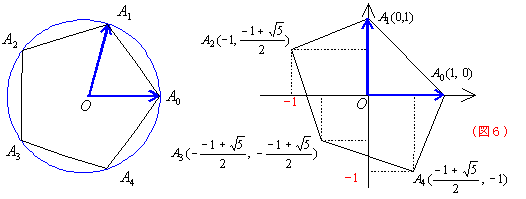
,![]() にするかで(新図)が違ってくる。同様に正5角形においても基底が
にするかで(新図)が違ってくる。同様に正5角形においても基底が![]() ,
,![]() にするか,
にするか,![]() ,
,![]() にするかで(新図)は違うのである。ここでOとは正多角形が内接している円の中心である。
にするかで(新図)は違うのである。ここでOとは正多角形が内接している円の中心である。