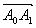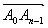このようにして求められた“変身多角形”には共通の重要性質があり，そのことについて調べてみよう。正n角形の“変身n角形”は，（元図）の基底が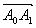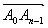，であるときはA_kが

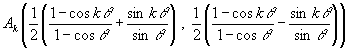
となるような“変身”をする。（この場合1≦k≦n−1）。

　また（元図）の基底が，であるときは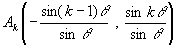となる。

　まず（元図）の基底が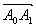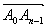，の場合から考えてゆくことにしよう。（新図）の各点は既に求められているが，A_kの（新図）での座標はA_k(x_k，y_k)としよう。このとき

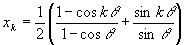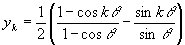　　　， となる。

　そこでA_k(x_k，y_k)とA_n-k(x_n-k，y_n-k)との関係を考えてみたい。　

　　　sin(n−k)θ= sin(nθ−kθ) = sin(2π−kθ)= sin(−kθ)=−sinkθ

　同様にcos(n−k)θ=coskθ　(∵)であることを利用すると

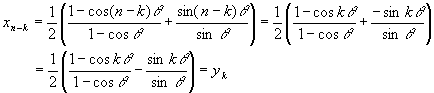
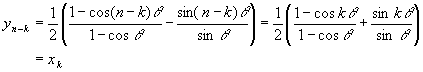
となる。従ってA_k(x_k，y_k)に対してA_n−k(x_n−k，y_n−k)はA_n−k(y_k，x_k)となっている。

　つまりA_kとA_n−kは直線y＝xに関して対称な点となっている。

　nが偶数のときk＝1，2，3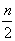，･･･，に対してn−k=n−1，n−2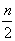，･･･，が対応し，A₁とA_n−1，A₂とA_n−2，･･･，ととがそれぞれy＝xに関して対称な点となり，のときはA_kとA_n−kとは同じ点となり直線y＝x上の点となる。

　またnが奇数の場合は，A₁とA_n−1，A₂とA_n−2，･･･，とがy＝xに関して対称な点となる。

　以上より“変身n角形”の図はy＝xに関して対称な図であることがわかる。

　次に（元図）の基底が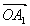，である場合について考えることにしよう。（新図）での点A_kは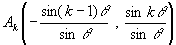でこれをA_k(x_k，y_k)とおく。

　このとき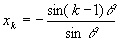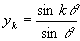，である。

　　sin(n−k−1)θ= sin(nθ−(k+1)θ) =−sin(k+1)θに注意しつつA_n−k(x_n−k，y_n−k)について調べてみよう。

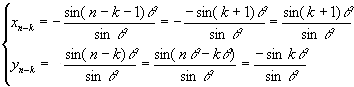
　またA_1+k(x_1+k，y_1+k)については

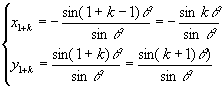
となっている。

　以上よりx_1+k=y_n−k，y_1+k=x_n−kとなりA_n−k(x_n−k，y_n−k)に対してA_1+k(x_1+k，y_1+k)はA_1+k(y_n−k，x_n−k)にとなり，A_n−kとA_1＋kとは直線y＝xに関して対称である。

　前と同様な考察により基底が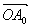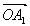，のときの“変身n角形”も直線y＝xに関して対称な図となる。

　またnが奇数のとき，1＋k=n−kよりは整数となり，A_n−kとA_1＋kとは同じ点となり，これは直線y＝x上の点となる。つまりnが奇数のときは直線y=x上にある。

　以上の性質は（元図）の正n角形を調べて導く事もできる。例えばnが偶数で基底が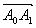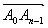，とする場合，線分A₁A_n−1，A₂A_n−2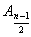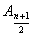，･･･，は互いに平行であり，それらの中点は直線A₀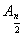の上にある。 1次変換fによってA₀と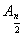をつなぐ直線は直線y=xに移され，A₁A_n−1の中点はこの直線上に移される。このことから（新図）がこの直線に関して対称であることを導く事ができる。また基底が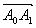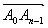，である場合，（新図）においては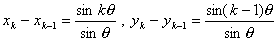の関係があり，これは図を描く際に役立つ性質といえる。