![]()

この夏は,本当に暑かった.講習受講中の生徒の顔も心なしかボーとしているかのように見える. 私は,この夏3年生の「看護希望数学(数Ⅰ・Ⅱ・A)」,「理系私大数学(北海学園大レベル)」の2コースの講習を持つことになった.本レポートは,講習中または講習後における生徒との対話から感じたことを気の赴くままに書き連ねたものである.本校では,「理系私大」といってもいわゆる"国公立は無理"という半ば「理系の○○こぼれ」~○○こぼし?~といったところで理系にも拘わらず何故か数学は苦手という子が多い.北海学園大レベルといっても基礎力の不足からこの時期に道工大の問題で数ⅠⅡABの復習を必要とする生徒達でである.数Ⅲなどはとんでもないといったところである.かえって,高看志望の生徒のほうが概してよく勉強する.そんな理系私大志望者の中にA子がいた.A子曰く「漸化式が全然わからない」.本レポートは,ここから始まる…
困った挙げ句にA子は来た.等差数列(A.P.),等比数列(G.P.)は,なんとか理解したという.止む無く以下のように,漸化式の概要を説明した.
●これ以外の問題は,この形に帰着させよ (Ⅰ)等差数列 |
案の定,(Ⅲ)で,分からない顔をしている.そこで,階差数列のイメージを出すために次のような説明を試みた.
元の数列 数列 {an} :2,5,10,17,26,37,50,65,…… ,( )
階差数列 数列 {bn} :3, 5, 7, 9,11,13,15,……,( )
を書き,次のような数直線イメージを使ってみた.数表記だけでは表現できないことも,図(シェーマ)は表現してくれる.生徒が自身の力でイメージを獲得すれば後は,積み重ねが可能だろう.

A子の苦難は,まだ続く.
次に隣接2項間の漸化式におけるG.P.化による解法を説明した.
特性方程式から特性解をもとめそれを利用して与漸化式を等比数列化する,あれである.
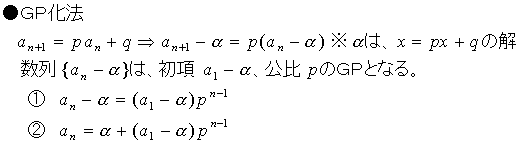 |
これが,また理解に苦しむようである.「なんで,いきなりαがでてくるの」.また,例題を解かせても①の段階でいきなり「 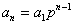 」としてしまう始末である.彼女の心情を察するとざっと以下のようになるのではないだろうか.
」としてしまう始末である.彼女の心情を察するとざっと以下のようになるのではないだろうか.
(ア) 変換した後の数列 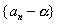 の状態が掴めていない の状態が掴めていない(イ) 等比漸化式からは,公比の情報のみ抽出することが理解できていない. |
(ア) については,次のような例を用いて再度説明した.(授業でも,講習でも同じように説明しているはずなんだが.「こいつまだ分からんのか!!」と思う心を静めつつ…)
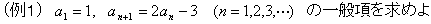 |
まずは,特性解などを意識せずに説明する.
私 :「これは,基本事項のどれに近い形かな」
A子:「……」
私 :「-3を隠すと,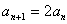 という,Ⅱの等比数列になるね.なんとか,公比3の等比数列に近い形にならないかな」
という,Ⅱの等比数列になるね.なんとか,公比3の等比数列に近い形にならないかな」
A子:「両辺に3を足すんですか?」
私 :「でも,それじゃあ左辺に3残っちゃうよ」
A子:「……」
私 :「(困ったぞ,えーい,まずイメージ作りからだ)これはね,魔法の数3(なんだそれ!)を使って,秘密数列を作ってこう考えるんだよ」と言いつつ,紙に次のように書いた.
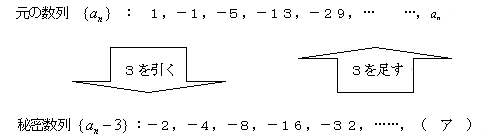 |
私 :「この秘密数列は,
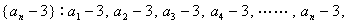
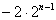 が入ります.」
が入ります.」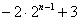 になります」
になります」(イ)については,以下のような特殊な例を挙げてみた,
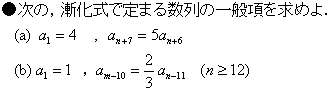 |
この他,口頭で何題かを答えさせていくうちに,漸化式の添え字が,「第何項か」という着眼点から「第何項と第何項の関係か」という視点になってきたようであった.
曲線の決定問題としては,漸化式で曲率が与えられ,初期値で曲線が確定する.ということなのだが生徒には添え字を変えられると困惑するようである.いっそのこと,「隣接2項」ではなく「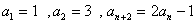 」のような nが奇数・偶数で異なってくる問題をどう解くのか見てみたい気がしてきた.
」のような nが奇数・偶数で異なってくる問題をどう解くのか見てみたい気がしてきた.
ここまでで,A子はG.P.化した数列を考えることで,元の規則性が不明な数列の一般項を求めるイメージができたようだ.あとは,ごまかした"魔法の数"について説明を加えておいた.数列 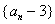 のイメージが掴め,その効力が理解できた為か,意外とすんなり理解できたようであった.
のイメージが掴め,その効力が理解できた為か,意外とすんなり理解できたようであった.
隣接2項間の漸化式は,ほぼ機械的に解けなくてはならない問題である. GP化法による解法は,一般の指数関数 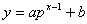 に位置する点列を,基本型の指数関数
に位置する点列を,基本型の指数関数 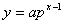 上の点列に変換して規則性を掴み取りやすくする操作である.しかし,変換自体の意図することをイメージすることなしにテクニックばかり習得しても隣接3項間の漸化式や,変形・置換を必要とする漸化式への応用力は育たないと思われる.数列分野は,「困難に出会ったら,まず今できることへ帰着できないかを考えよ」という思考法の鍛練の場をしての視点を忘れずに指導していきたいものである.
上の点列に変換して規則性を掴み取りやすくする操作である.しかし,変換自体の意図することをイメージすることなしにテクニックばかり習得しても隣接3項間の漸化式や,変形・置換を必要とする漸化式への応用力は育たないと思われる.数列分野は,「困難に出会ったら,まず今できることへ帰着できないかを考えよ」という思考法の鍛練の場をしての視点を忘れずに指導していきたいものである.