札幌藻岩高等学校 菅原 満
全５種類のいわゆる"プラトンの立体"の塗り分けの総数を計算してみよう．考え方の方針は「１色を固定して考える」ことである．
まず４色のうち１色を底面に固定して，残りの３側面は回転による重なりを考慮して円順列で計算する．
結果は ∴ (3-1)!=2通り
まず６色のうち１色を底面に固定して次のように計算していく．
①１色を底面に固定して，反対側の面の色を決める ⇒ 5通り
②残った４側面の塗り分けは，回転による重なりを考慮して円順列で ⇒ (4-1)!=3!=6通り
③ ①，②より，求める塗り分けの総数は ∴ 5×(4-1)!=30通り
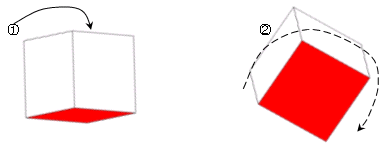
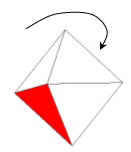
① 1. 2.と同様に１色を固定して考えてみる．反対面を塗る方法 ⇒ 7通り
② ここで，残った６つの側面を塗り分ける ⇒ (6-1)!=5!=120通り
本当にこれでいいのであろうか？ 底面に辺を接する３つの正三角形と頂点が接する３つの正三角形がある．これらは塗り分けに関して"同等"
であろうか？ 答えは"否"である．
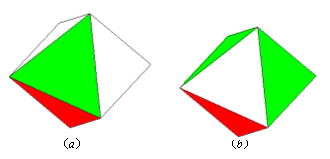
下図（a），（b）では，塗り分けにおいて明らかな違いがある．
このことを修正するために②部分は，次のようになる
{6C3×(3-1!}×3!=6・5・4/3!×2!×3!=240通り または(6-1)!×2=240通り
従って，求める正８面体の８色による塗り分けは ∴ 7×240=1680通り となる．
これは，某社の問題集の解答でも「7×5!=840通り」とある通り見落としやすい問題である．
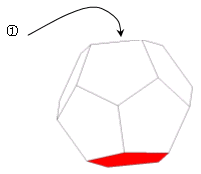
① １色を固定して考えてみる．反対面を塗る方法 ⇒ 11通り
② 残った10側面のうち固定した底面に辺を接する5個と接していない5つの面に分けて塗り分けると 10C5×(5-1)!×5!=725760
従って，求める正12面体の12色による塗り分けの総数は 11×725760=7983360通り
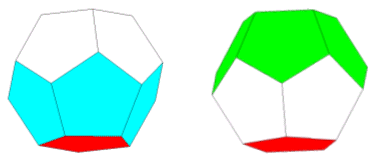
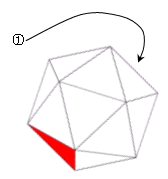
① １色を固定して考えてみる．反対面を塗る方法 ⇒ 19通り
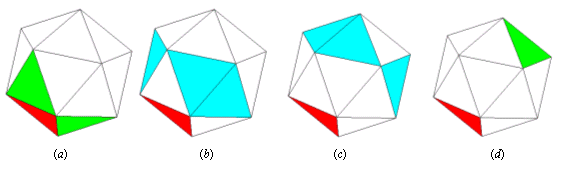
② 残った18の側面を下図の(a)，(b)，(c)，(d)に分けて数え上げると
18C3×(3-1)!×15P6×9P6×3!=2134124568576000
従って，求める正12面体の12色による塗り分けの総数は
19×2134124568576000=405483668029440000通り
となる．
正多面体は５種類しか存在しないことは周知のことであるが，このように５種類の正多面体の塗り分け問題を考える中で，「これほど均整のとれた美しい正多面体の計算はもっと美しくあるべき」という考えが頭をもたげてきた．つまり，正n面体ならば，「n！」から求めたいのである．
(1)「正方形の各辺を４色の異なる絵の具で塗り分ける方法の総数は何通りか」という問いに対しては，
４というKeyNumberを使って 4!/4=(4-1)!=6 通り という明快な解を得ることができる．
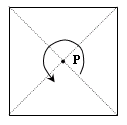
これは，1～5までで用いた１色を固定して"回転を止める"という見方もあるが， 正方形のもつ対称点Pを考えると，
「求める塗り分けの総数をNとすると，Pに関する回転を考慮して 4!=N×4 ∴N=4!/4」
(2) 正多面体の場合～回転軸と頂点の次数を使った一般化
正多面体の場合はどうなるか．例として正４面体を考えてみよう．
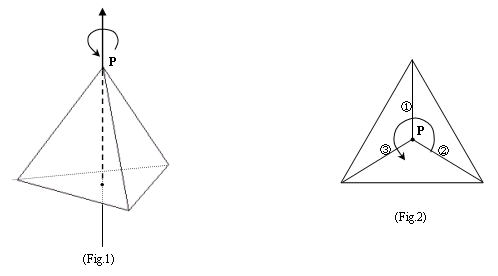
異なる4色による塗り分けの総数をNとする．この"N"と"4！"の関係を考えてみる．回転軸は正４面体の場合頂点から底面へ垂線を下ろすことで頂点の個数４本存在する．２次元平面での回転の中心(点)に対して，３次元立体の場合は回転軸(直線)となる．この際，この軸には向きを考えておく(Fig.1)．
また，頂点Pでは正４面体の場合３つの辺が接している．この頂点で接している辺の数を"頂点の次数"と呼ぶことにする．
例としてFig.2で頂点Pにおける回転を考える．4！の塗り分けのうち，回転により頂点の次数だけ同じものが存在する．これらは他の3つの回転軸についても同様である．従って次の式を得る．
|
4!=N×(回転体の本数)×(頂点の本数) =N×(頂点の数)×(頂点の次数) ∴N=4!/(頂点の数)×(頂点の次数)=4!/(4×3)=2通り |
この考え方は，残りの４つの正多面体に対しても適用できるだろうか．確認してみよう．
５種類の正多面体について，この考えを適用してみたものが下表である．
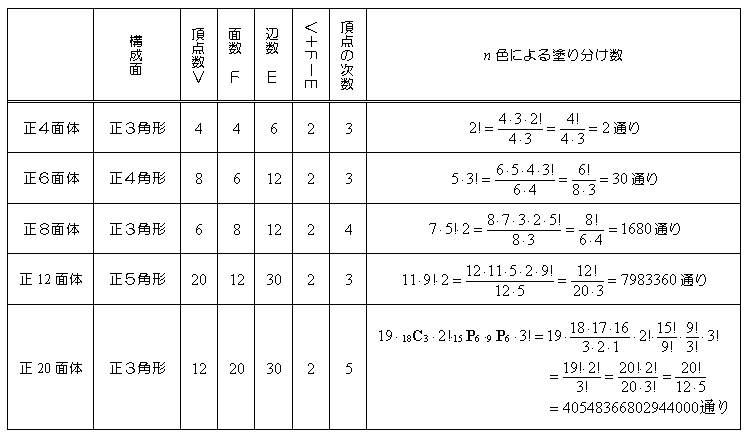
ここまでの過程で，正n多面体の異なるn色による塗り分けの総数に関して次の結論を得た．
正n面体を異なるn色の絵の具で塗り分ける総数Nは |
| （余談１）
|
ケプラーの生きた当時は地球のほか水星･金星･火星･木星･土星の5惑星しか発見されていませんでした．ケプラーはこの惑星の数"５"とプラトンの立体の数"５"に霊感(?)を感じて次のような宇宙観(理想)を作り上げていたようです． 「地球の軌道は、全ての軌道の尺度である。これに正十二面体を外接させよ。するとこの立体を囲むその球が、火星の軌道となるだろう。火星の軌道に正四面体を外接させよ。するとこの立体を取り囲むその球が木星の軌道となるだろう。木星の軌道に立方体を外接させよ。この立体を取り囲むその球が、土星の軌道となるだろう。また地球の軌道には正二十面体を内接させよ。この立体に内接するその球は、金星の軌道となるだろう。金星の軌道に正八面体を内接させよ。するとこの立体に内接するその球が水星の軌道となるだろう。」 図式化すると下記のようになります． ○水＜正8面体＜○金＜正20面体＜○地＜正12面体＜○火＜正4面体＜○木＜正6面体＜○土 |
| （余談２） |
上の表をじっと眺めていると，ケプラーではなくとも奇妙な数字の対応関係に気がつきます． 面数(F)と頂点数(V)の対応です． 正４面体⇔正４面体，正６面体⇔正８面体，正12面体⇔正20面体 これにより，たとえば正12面体の各面の中心で内接する正20面体が存在することがわかります． これを，多面体の双対関係といいます． How beautiful |
（Notes）「正多面体が５種類しか存在しない」ことのお話
| 定義）正多面体～各面が同じ正多角形で各頂点の構成が等しい多面体 |
上の定義により正四面体を２つ重ねた(Fig.3)は各頂点での次数が3,4と異なるため正多面体にはなりません．
正多面体に限らずどんな多面体についてもオイラーの定理が成り立ちます．
【オイラー(Euler)の定理】
|
多面体の頂点の個数(V)，面の個数(F)，辺の個数(E)とすると V＋F－E＝2 |
この定理を使って正多面体が５つしか存在しないことを示しましょう．
多面体の場合，１つの頂点に集まる面の数は３以上でなければなりません．また，各面の頂角の和は2πより小さくなることが必要です．
正n角形の内角はπ-2π/nですから，次の構成する面について次の不等式を満たす必要があります．
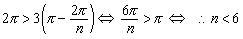
よって，各面を構成する正n角形は，n＝3，4，5の場合だけを考えればよいことになります．
(ⅰ) n＝3の場合．正多面体を構成する面は正三角形となります．
頂点に集まる面の数をxとすると，x=3,4,5の場合が考えられます．
(ｱ) x=3の場合
正N角形があるとすると面の数はN個，辺の数は3Nですが，各辺が2つの面により構成されますから 3N/2本あり，頂点は3N個ですが，各頂点は3つの面により構成されますから3N/N=N個あることになります．オイラーの公式でV=N,F=N,E=3N/2として代入すると
N+N-3N/2=2 ∴ N=4
となり正４面体となることが分かりました．
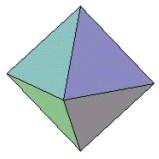(ｲ) x=4の場合
正N角形があるとすると面の数はN個，辺の数は3Nですが，各辺が2つの面により構成されますから3N/2本あり，頂点は3N個ですが，各頂点は4つの面により構成されますから3N/4個あることになります．オイラーの公式でV=3N/4,F=N,E=3N/2として代入すると
3N/4+N-3N/2=2 ∴ N=8
となり正８面体となることが分かりました．
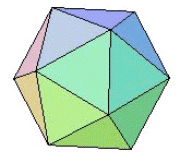(ｳ) x=5の場合
正N角形があるとすると面の数はN個，辺の数は3Nですが，各辺が2つの面により構成されますから3N/2本あり，頂点は3N個ですが，各頂点は5つの面により構成されますから3N/5個あることになります．オイラーの公式でV=3N/5,F=N,E=3N/2として代入してみると
3N/5+N-3N/2=2 ∴ N=20
となり正２０面体が導かれます．
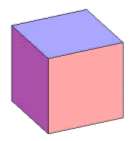(ⅱ) n＝4の場合．正多面体を構成する面は正方形となります．
この場合，頂点に集まる面の数は3個になります．正N角形があるとすると，面の数FはN個，頂点の個数Vは4N/3個，辺の数Eは4N/2=2N本となります．
オイラーの公式へ代入すると，
N+4N/3-2N=2 ∴ N=6
となり正６面体が得られます．
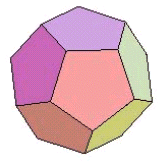(ⅲ) n＝5の場合．正多面体を構成する面は正五角形となります．
この場合，頂点に集まる面の数は3です．正N角形があるとすると面の数FはN個，頂点の個数Vは5N/3個，辺の数Eは5N/2本となります．
オイラーの公式へ代入すると，
N+5N/3-5N/2=2 ∴ N=12
となり正１２面体が得られます．
以上のことから，正多面体は正４面体，正６面体，正８面体，正12面体，正20面体しかないことが分かります．
なお，オイラーの定理の証明は，多面体が柔らかい伸縮する膜でできていると考えて，どこか一面に穴を開けて引っ張り平面状に伸ばして考えます．V，Eは不変でFは１減りますからオイラー標数が平面で１になることを示すのです．伸ばして平面上にした多角形グラフを三角形に分割し，分割してからどんどん減らしていくというのが要点になります．是非，考えてみてください．
