我々は日々の授業の中で，進度に追われるように授業を進めている．１年生ならば数�T・Ａと教材を配列し演習を取り入れ何とか定着を図る．生徒に教材の本質的理解を求めながらも「証明よりも，まずこれを使えるようにすることが大切だ．その後に事の本質は否応なく見えてくるよ」などと，本当のような嘘のような事を言いながら．

　我々は定理の導入背景や，証明のアイディアと流れを重視する．しかし，生徒はその中の詳細な数式の暗記に走る．まるで，私が大学時代にε−δ論法による証明を見て「何故最後は“＜ε”で終わるのだろう“＜4ε”ではだめなのか」と意味もなく悩んだように．そして，それが単に証明の格好をつけているだけと分かったときの虚しかったこと．Cauchyの時代よりEulerの時代の方が数学は生き生きしていたのではないかと感じたりもする．正に生徒は，このような何でもないことで悩んでいるのではないだろうか．物事の本質が分かればその利用法は自ずと見えてくるのではないだろうか．しかし，一方からのみの視点では事の本質らしきものすら見えてこない．様々な角度から教材を眺めることで，新たな一面が見えてくるものである．

　数学�Tにおける２次関数は，変化率が一定でないごく身近な関数の代表例として登場する．放物線については関数の最大・最小，方程式，不等式を解いていく時の補助手段としての性格が強く「放物線」の２次曲線としての図形的考察は数学Ｃまで待たねばならない．また放物線を描くときには平方完成による方法が主体であり,現行の学習指導要領では放物線とx軸の交点のみで一般の直線との交点は範囲外である．

　前述したように一つの教材に対して「様々な視点からのアプローチ」は重要である．

　ここでは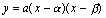，という切片形からのグラフ指導の展開や放物線と直線線で囲まれた面積に注目したときの放物線の性質などを考えてみたい．

　２次関数のグラフは，普通は次のような指導経過をとる．

　前回の研究会で新川高校の中村先生により「和関数」という考え方で，(6)の一般型における係数のグラフに対する寄与，斜交座標系への変換（等積変換）などのレポートがあった．その際「いっそのこと，(3)の基本型の説明の後，(6)の切片形からのグラフ指導はできないものか」と考えてみたのがきっかけである．

　実際は，一通り4次関数が終えた後に，別の視点からのアプローチとして提示した方がよいと思われる．