

本レポートはパラメータを含む2次関数の最大・最小というオーソドックスな教材についてです.〜閑話休題〜 鉛筆の持ち方が気になる.いわゆる"親指オーバーハング現象"である.テスト監督をしているとき数えてみると16人が"ハーフオーバー"で3人が"完全オーバー"でありいわゆる"秘技ドラエモン"持ちであった.
この件を小手技シリーズで有名なN先生と話していると「爪の伸ばしている女子」というN先生らしい分析であった.皆様の学校の生徒はいかがでしょう?この現象が学習定着などと相関があるかどうかはいまだ不明です...
| 時間 | 内 容 | 備 考 |
| 5分 | ○前時の復習〜基本事項の整理 Level.1 定義域に制限なし Level.2 定義域に制限あり ※最大・最小〜yの値に着目 |
※黒板左にまとめる |
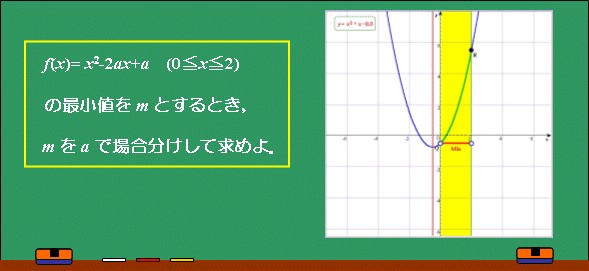
| 15分 | Q3.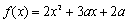 の最小値をm の最小値をm(1)最小値mをaで表せ (2)m(a)の最大値を求めよ →シミュレーションによりイメージ化 |
問題文の読解 ・定義域制限の有無を確認 ・平方完成 |
| 20分 | Q4.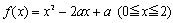 (1) 最大値Mの場合分け →シミュレーションによりイメージ化 (2) 最小値mの場合分け →シミュレーションによりイメージ化 |
問題文の読解 |
| 10分 | 板書でまとめる | シェーマの提示 |
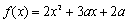 の最小値の最大値を求める ■■■
の最小値の最大値を求める ■■■
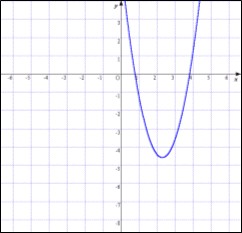
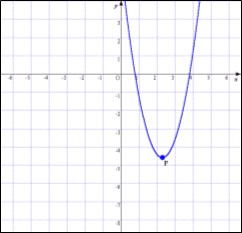
| (Fig.1) グラフの概形表示 | (Fig.2)頂点を表示 |
 |
 |
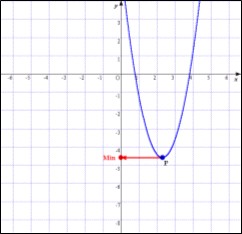
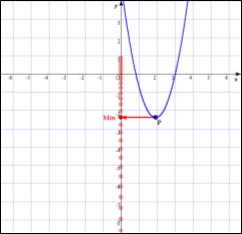
| (Fig.3)値域の最小値をマークアップ | (Fig.4)パラメータを変化させてm(a)の変化を表示 |
 |
 |
(1)Grapesの設定
【関数定義】[f(x)=]2x^2-3ax+2a
【陽 関 数】[y1=]f(x)
【基本図形】
| (図形P〜頂点) | (図形S〜Min) | ||
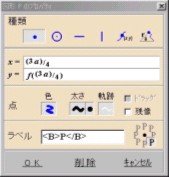 |
[座 標] [x=](3a)/4 [y=]f((3a)/4) [ラベル]<B>P</B> |
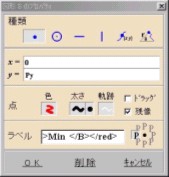 |
[座 標] [x=](3a)/4 [y=]Py ※Py〜点Pのy座標 [ラベル]<RED><B>Min </B></RED> |
【線分】
 |
左のアイコンをクリックし点Sから点Pへ線分を指定し→の向きはP→Sとなるように指定する. |
(2)シミュレーションにあたって
 より効果的に提示するには,工夫が必要である.
より効果的に提示するには,工夫が必要である.
以前,北数教の発表レポートの時は「Multi Frame」すなわち,提示情報の細分化に応じGrapesのファイルを分割してシミュレーションを行っていた.しかし現在のversionでは,関数・基本図形など表示・非表示の切り替えが可能なため1ファイルで同様の効果を得ることができる.
実際の授業においてはこの機能を活用したほうが便利である.
具体例を示す.右上図ではPは表示,QとSは非表示である.図形を示すシンボルをクリックすることでトグルで表示・非表示が入れ替わる.授業において生徒に強調したいことを分析して,この操作によって必要な図形だけを表示すればよい.
この教材では,次の表示順にしてみた.③において頂点Pを表示したときy軸への射影も同時に表示するようにしてみた.これについては(1)を参照していただきたい.
①陽関数
②頂点(P)
③Pのy軸への射影(S) ※このときPからSへの→も同時に表示
 また,残像の表示・非表示も可能である.
また,残像の表示・非表示も可能である.
右の例では残像は非表示の状態である.パラメータを変化させて確認した後で残像表示可能としてm(a)の変化の推移をマークアップする.
Grapesのメモ,ラベルはテキストだけではなく式,式の値なども表示できHTML同様のタグで文字装飾も可能となっている.
以下,ヘルプファイルより抜粋
【文字装飾】
|
(1)Grapesの設定
【関数定義】[f(x)=] x^2-2ax+a
【陽 関 数】[y1=] f(x)(x<t or t+2<x) [色]青
[y2=] f(x)(t<=x<=t+2) [色]緑
[y3=] f(x) [色]青
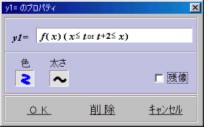
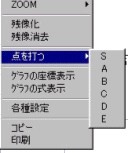
【基本図形】
(豗)定義域内の比較すべき点を設定する.なお,頂点は定義域内のときのみ表示する
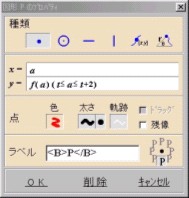
(頂点P) [種類]点,[x=] 1,[y=] f(x)(t<=a<=t+2),[色]青,[ラベル]<B>P</B> 下に表示
(端点Q) [種類]点,[x=] t+2,[y=] f(t+2),[色]青,[ラベル]<B>Q</B> 右下に表示
(端点R) [種類]点,[x=] t,[y=] f(t),[色]青,[ラベル]<B>R</B> 左下に表示
( 軸 ) [種類]縦線,[x=] a,[色]赤
(豩)定義域を帯状に表示する
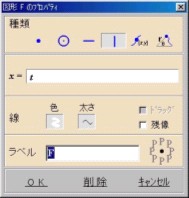
①(直線x=t)[種類]縦線,[x=]t,[色]白
②(2,2)付近にマウスを持っていき右クリックから点Gを打つ※右図参照
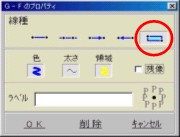
③"2点を結ぶ"をクリックして点Gから直線x=tに線分を引き,線種を矩形,領域を黄色にする.
④点Gのx,y座標を変更しGをグラフ外へ移動する. [x]t+2,[y]30
※陰関数を利用して0≦x≦2などとしてもハッチングで表示でき固定領域の場合は有効である.本問題では領域を移動するためより高速な上記の方法が有効である.

(豭)MaxUFO,MinUFOの表示
Max,Minの表示は,シェーマによる説明とリンクさせる.藻岩高校 中村先生の「ドメインUFO」のアイデアに相乗りさせていただいた.
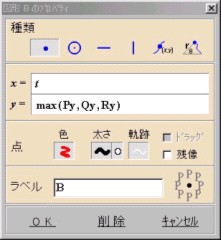
| (MaxUFO) | (Max左端点)[x] t,[y] max(Py,Qy,Ry) [色]赤,[太さ]○ (Max右端点)[x] t+2,[y] max(Py,Qy,Ry) [色]赤,[太さ]○ 2点を作成後"2点を結ぶ"をクリックして2点を極太(赤)の線分として結ぶ. [ラベル] <red><B>Max</B></red> [表示位置]上 ※<red><B>Max= !{By}</B></red> とすれば点Bのy座標の値すなわち最小値を表示することもできる.今回は情報量が多くなり過ぎるため入れなかった. |
| (MinUFO) | (Max左端点)[x] t,[y] min(Py,Qy,Ry) [色]赤,[太さ]○ (Max右端点)[x] t+2,[y] min(Py,Qy,Ry) [色]赤,[太さ]○ 2点を作成後"2点を結ぶ"をクリックして2点を極太(赤)の線分として結ぶ. [ラベル] <red><B>Min</B></red> [表示位置]下 |
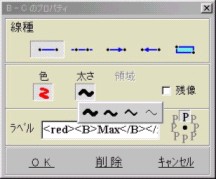
【ラベル・メモにおける式と式の値の表示〜ヘルプファイルより抜粋】
|
(3)授業展開について
(豗)シミュレーションにより教材のイメージ化を図る
この時の重点は"最大値(最小値)をどこでとるか"という点に着目させることである.
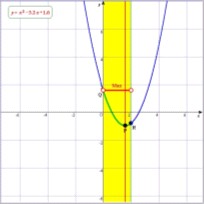
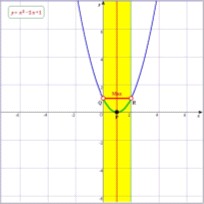
この点を強調するために,定義域の幅をもつ線分(ドメインUFO)に登場してもらう.パラメーターを変化させこのUFOが放物線と接触する点(最大値)の位置に着目させる.
(左端)→(両端)→(右端)と変化することが見てとれる.ここで強調すべきは,大きく2つに場合分けされるという点を強調してその分岐点となっているのがFig.6であることを確認する.
次のシェーマによる説明のために,グラフを固定して定義域を動かしてUFOと放物線の接点の変化をシミュレーションしてみる.グラフの上下変動はあるがUFOが放物線と接触する点(最大値)の位置についてはグラフと定義域の左右の位置関係が重要であることを理解できればUFOには退散願うこととなる.
 |
 |
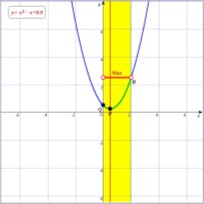 |
| (Fig.5) | (Fig.6) | (Fig.7) |
(豩)シェーマによるまとめ
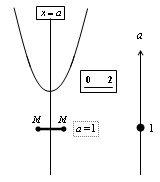
ここで活躍するシェーマはFig.8である.シェーマには分岐点となるUFOを降下させて表示する.このときのパラメータaの値をUFOの右横に書く.
ここでa=1 によって場合分けをすることになる.この際,このシェーマの右横に上向きの座標軸(a軸)を入れることも有用である.もちろんa軸が上向きか下向きかは問題によって変化する.
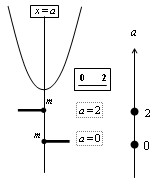
最小値においても同様のシミュレーション,シェーマによるまとめを行う.
提示したシェーマはFig.9である.
解答としてまとめるときは,最大値・最小値で場合分けをして列記するよう指導している.
 |
 |
| (Fig.8) | (Fig.9) |
|
|
(4)解答のまとめ方についての一考察
「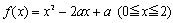 の最大値・最小値を求めよ」という問題の解答の書き方については,パラメータaにより場合分けをして,最大値・最小値を併記していく解答が多いように思う.
の最大値・最小値を求めよ」という問題の解答の書き方については,パラメータaにより場合分けをして,最大値・最小値を併記していく解答が多いように思う.
これは"Max,Min"という2つの値の変化を同時に考える必要があり初期の段階では問題をより複雑化しているようである.私の場合は,まずMaxとMinに大きく分けて,それぞれパラメータaで場合分けして解答するように指導している.パラメーターaについて場合分けをして解答を書くのはこれらに習熟してからでも遅くはない.性急にまとめようとするとせっかくイメージ化されて定着した部分すら失われてしまう恐れすら感じている次第である.
『指導解答例』
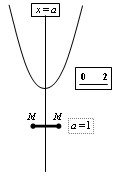 |
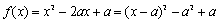 ∴軸x=a ∴軸x=a |
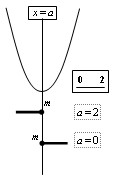 |
|
| 1°最大値 (豗) 1<aのとき x=0で最大値f(0)=a (豩) a=1のとき x=0,2で最大値0 (豭) a<1のとき x=2で最大値f(2)=4-3a |
2°最小値 (豗)2≦aのとき x=2で最大値f(2)=4-3a (豩) 0≦a<2のとき x=aで最小値f(a)=-a2+a (豭) a<0のとき x=0で最小値f(0)=a |
||