

(1)概念の導入方法
内分と外分は,生徒にとっては理解はできるがよく間違える概念のようです。
まず分点の位置がわからない。そこで,ABの分点Pは,Aを出発してPを経由してBへ至るときの歩数の比を求めるように考えさせています。もし,線分ABの中で済めば内分,その線分から外へはみ出したら外分と考えるのです。
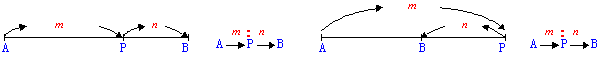
次に生徒が間違うのが,分点公式です。特に平面上の点となると,公式を覚えてはいても,x成分にy成分を代入するといった間違いまで出てきてしまいます。その解決には,ベクトルの計算方法を導入する方法がよいようです。
 点A(x1,y1)点B(x2,y2)をm:nに内分する点Pの座標は,
点A(x1,y1)点B(x2,y2)をm:nに内分する点Pの座標は,
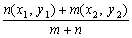
となります。
この計算の利点はたとえば次のような問題の時に発揮されます。
| 例1 線分ABを3:2に内分する点をPとする。A(1,-3),P(-5,6)とするとき,Bの座標を求めよ。 |
 B(x,y)とすると,
B(x,y)とすると,
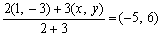
(2,-6)+3(x,y)=(-25,30)
3(x,y)=(-27,36)
(x,y)=(-9,12)
よってB(9,12)
これは,BがAPを5:2に外分する点であると読み替えたり,従来の成分ごとに計算する方法よりも定着がよかったように思います。
(2)期待値と食塩の濃度
さて,この分点の公式を,数直線上で考えてみます。
ある生徒が,テストを受けた時に,a点,b点をそれぞれm回,n回取ったとする。この生徒が次回にテストを受けたときにとる点の期待値はいくらか。という問題の解は,
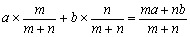
となります。
これは,数直線上の点A(a),B(b)を結ぶ線分をn:mに内分する点の座標と同じですが,これはまた数直線ABの点A,Bにそれぞれ,mグラム,nグラムの重りを吊り下げたときのつりあいの点に一致します。
実際に,つりあいの求める点の座標をxとすると,力のモーメントから
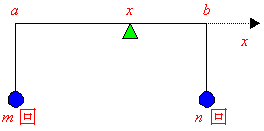 m(x-a)=n(b-x)
m(x-a)=n(b-x)
mx-ma=nb-nx
(m+n)x=ma+nb
![]()
であるからです。
このように考えると,分点公式=期待値=平均値=つりあいの値,といったイメージ化ができるように思います。
この考えを食塩の濃度の問題に適用すると,a%の食塩水がmグラム,b%の食塩水がnグラムあり,これを混合させたときの濃度は,
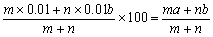
となりますから,内分公式と,つりあいを考えて食塩の問題を解くことができます。
| 例2 5%の食塩水を100グラムと9%の食塩水300グラムを混合させたときの濃度はいくらか。 |
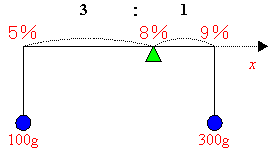 A(5),B(9)にそれぞれ100グラムと300グラムの重りをぶら下げたときのつりあいを考えて,ABを3:1に内分する点の座標を求めると,
A(5),B(9)にそれぞれ100グラムと300グラムの重りをぶら下げたときのつりあいを考えて,ABを3:1に内分する点の座標を求めると,
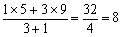
となるから 8%。
勿論水を加えたときは濃度0%,食塩を加えたときは濃度100%として計算します。
(3)メネラウスの定理
数直線上で,点に重さを加えることで内分点をつりあいとしてイメージしたことを,平面上に拡張することもできます。メネラウスの定理は,ベクトルの分点を求めるーつの方法として利用されていますが,次の問題を解いてみます。
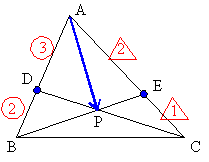 例3 三角形ABCの辺ABを3:2に内分する点をD,辺ACを2:1の比に内分する点をEとし,線分CDとBEの交点をPとする。 例3 三角形ABCの辺ABを3:2に内分する点をD,辺ACを2:1の比に内分する点をEとし,線分CDとBEの交点をPとする。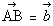 , ,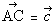 とするとき, とするとき,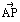 を を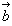 , ,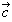 を用いて表せ。 を用いて表せ。 |
解としては,BP:PE=2:1,CP:PD=5:4を求め,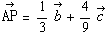 と出すのが一般的ですが,これは,点Aに2,点Bに3,点Cに4の重りを置いたときの重心を求めることに一致します。
と出すのが一般的ですが,これは,点Aに2,点Bに3,点Cに4の重りを置いたときの重心を求めることに一致します。
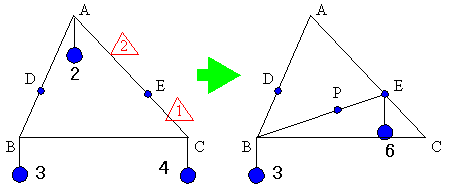
この時,点Aと点Cのトータルは,点Eへ6の重りを置いたことになり,3点ABCのつりあいは,点Bと点Eのつりあい,つまり線分BEを6:3=2:1に内分する点がこの三角形の重心になります。
よりー般的に三角形ABCの辺ABをa:bに内分する点をD,辺ACをc:dの比に内分する点をEとすると,点Aにはbd,点Bにはad,点Cにはbcの重りを置けば,点Eには(c+d)bの重りを置いたことになり,BP:PE=(c+d)b:adとなるので,この考え方の妥当性が証明されます。
というのは,メネラウスの定理から,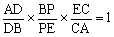 より
より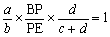
よって,BP:PE=(c+d)b:ad となるからです。
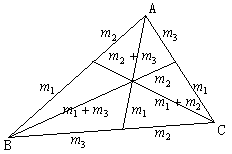 逆に,Aにm1,Bにm2,Cにm3の重りをつり下げると,たとえばEはACをm3:m1に内分する点になり,m1+m3の重りが置かれたことになり,PはBEを(m1+m3):m2に内分する点であり,A(
逆に,Aにm1,Bにm2,Cにm3の重りをつり下げると,たとえばEはACをm3:m1に内分する点になり,m1+m3の重りが置かれたことになり,PはBEを(m1+m3):m2に内分する点であり,A(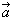 ),B(
),B(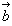 ),C(
),C(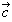 )とするとPの位置ベクトルは
)とするとPの位置ベクトルは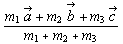 であることがわかります。
であることがわかります。
これも平均やつりあいのイメージである式ではないでしょうか。
更に例えば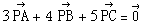 をみたす点をPを決定せよ,という問題は,Aに3,Bに4,Cに5の重りを置いたときのつりあいの点がPであることも子の式からわかります。
をみたす点をPを決定せよ,という問題は,Aに3,Bに4,Cに5の重りを置いたときのつりあいの点がPであることも子の式からわかります。
閑話休題,このメネラウスの定理は非常に書きにくいところです。上の問題では,三角形ABEに直線CDが関係していると考えて解いていますが,なかなか見つけにくいのではないでしょうか。
そこで,私は,比を知りたい頂点から出発して,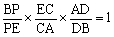 と教えています。
と教えています。
内分×外分×内分=1と覚えます。ついでにチェバの定理は 内分×内分×内分=1というわけです。
![]() 円の接線
円の接線
円の接線の問題は判別式を使うより,中心と直線の距離を半径と比較したほうが計算は容易です。
ここで問題となるのは,x,yの値がすぐに出ないということです。これを出すのであれば,判別式の方が早いように思われます。しかし次のように考えてはどうでしようか。
| 例4 x2+y2=25のとき,x+2yの最大,最小とそのときのx,yの値を求めよ。 |
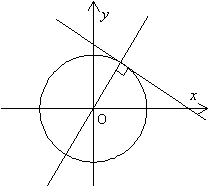 解 x+2y=kと置く。直線x+2y=0と円x2+y2=25が接するときを考えると,原点と直線の距離が半径に等しければよいから,
解 x+2y=kと置く。直線x+2y=0と円x2+y2=25が接するときを考えると,原点と直線の距離が半径に等しければよいから,
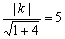 より k=±5
より k=±5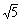
として最大・最小は出ます。このとき, x,yの出し方は,一般的には x+2y=±5 とx2+y2=25の連立方程式を解きますが,これがめんどうくさいのです。気の利いた参考書では,x+2y=±
とx2+y2=25の連立方程式を解きますが,これがめんどうくさいのです。気の利いた参考書では,x+2y=±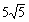 とこの直線に垂直で原点を通る直線2x-y=0との交点を求める方法が記されています。
とこの直線に垂直で原点を通る直線2x-y=0との交点を求める方法が記されています。
(1)接線の公式の逆
しかし,この問題はもっと容易に解けます。それは,
x2+y2=r2における接線x1x+y1y=r2の接点が(x1,y1)である
ということを使います。この証明は容易です。すなわち,もし (x2,y2)を接点とするならば,接線の公式から,x2+y2=r2 が接線の式になりますが,これがx1x+y1y=r2と恒等的に等しいことから(x2,y2)=(x1,y1)
すなわち,接線の公式の逆が成り立つことになるのです。そこで次のような解法が生まれます。
解2 x+2y=5 の両辺を5 倍して,
倍して, x+2
x+2 y=25
y=25
よつて接点は( ,2
,2 )となりx=
)となりx= ,y=2
,y=2 のとき最大値5
のとき最大値5 を得ます。同様に,x=-
を得ます。同様に,x=- ,y=-2
,y=-2 のとき,最小値-5
のとき,最小値-5 となります。
となります。
(2)媒介変数と合成
また,媒介変数を使った次のようなやり方も考えられます。
x=5cosθ,y=5sinθとおいて,x+2y=10sinθ+5cosθ=5 sin(θ+α)
sin(θ+α)
(sinα=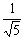 ,cosα=
,cosα=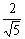 これが大事)
これが大事)
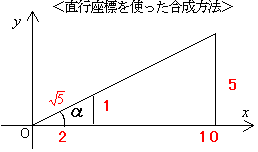
最大値は θ+α=90°のとき。よって
x=5cos(90°-α)=5sinα= ,y=5sin(90°-α)=5cosα=2
,y=5sin(90°-α)=5cosα=2
最小値もθ+α=270°から同様に
x=5cos(270°-α)=-5sinα=-
y=5sin(270°-α)=-5cosα=‐2
のとき となります。
話はそれますが,この,媒介変数による方法の逆を使うと,合成問題が容易に解けます。
例5 sinθ+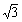 cosθ=1 (0°≦θ<360°)をとけ。 cosθ=1 (0°≦θ<360°)をとけ。 |
解1 2sin(θ+60°)=1 よりx=θ+60°とおくと 60°≦xく420°でsinx=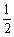 より
より
x=150°,390° よって θ=90°,330°
解2 x=cosθ,y=sinθとおくと,y+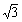 x=1より,θ=90°,330°
x=1より,θ=90°,330°
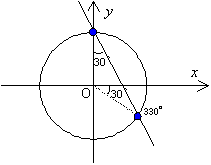
不等式も容易に,
例6 sinθ+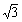 cosθ>1 (0°≦θ<360°)をとけ。 cosθ>1 (0°≦θ<360°)をとけ。 |
というのは,上のグラフから,0°≦θ<90°,330°<θ<360°となります。
(4)コーシー・シュワルツの不等式
最近はあまりお目にかからないようですが,シュワルツの不等式を使う方法もあります。
(12+22)(x2+y2)≧(1x+2y)2 から 5×25≧(1x+2y)2 ∴ -5 ≦x+2y≦5
≦x+2y≦5
等号は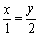 のときだからx+4x=5
のときだからx+4x=5 ,x=
,x= ,y=2x=2
,y=2x=2 を得ます。最小値も同様にできます。
を得ます。最小値も同様にできます。
(3)正接によって傾きを得る方法
曲線外からの接線の問題は次のように解くこともできます。
| 例7 円 x2+y2 =25への,点A(1,7)からの接線と接点を求めよ。 |
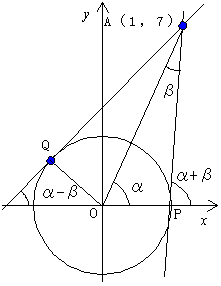 接点をP,Qとする。∠AOx=α,∠AOP=βとすると,
接点をP,Qとする。∠AOx=α,∠AOP=βとすると,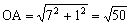
OP=5より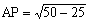 よって tanα=7,tanβ=1
よって tanα=7,tanβ=1
このときAPの傾きは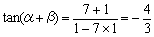 であるから
であるから
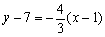 3y-21=-4(x-1) 4x+3y=25
3y-21=-4(x-1) 4x+3y=25
接点は(4,3)となります。
同様に,AQの傾きは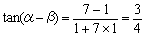 であるから,
であるから,
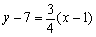 4y-28=3(x-1) 3x-4y=-25
4y-28=3(x-1) 3x-4y=-25
接点は(-3,4)となります。
![]() 条件付き確率
条件付き確率
条件付き確率のなかには,むしろ場合の数を数えたほうがよい場合もあります。
| 例8 10本のくじがあり,このうち3本があたりである。引いたくじを戻さずにA,B,Cがこの順にくじを引くとき,Cがあたる確率はいくらか。 |
ほとんどの教科書や参考書は,次のように解いています。
3人ともにあたりのとき 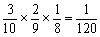
A,Cがあたりのとき 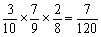
B,Cがあたりのとき 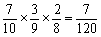
Cがあたりのとき 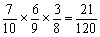
以上は排反であるから, 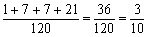
これを,次のように考えます。
くじに番号が書いてあるとして,1から3があたり,4から10がはずれだとします。A,B,C3 人がくじを引いてそのくじを並べたときに,3 番目にあたりがくる場合の数は,3×9×8通りですから,確率は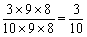 となります。
となります。
つまりこれは,
カードを3枚並べて3桁の数を作るときに,一の位が1から3になる確率はいくらか
という問題と同じです。であれば,はじめに,1の位にカードを1から3までのカードを置く確率を考えると,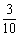 であるということが出きます。
であるということが出きます。
また,A,B,Cのひいたくじの番号を並べて,(x1,x2,x3)⇔(x3,x2,x1)によって1対1に対応させるともれなく対応するから,AとCのあたる場合の数は同じである。よって確率も同じである,という考え方もできます。
前者の考え方をすると,
| 例9 例8と同じ条件でくじを4人が引いたときに,4番目の人があたりを引いた。このとき 3番目の人がはずれを引いている確率をもとめよ。 |
4番目に1から3のどれかのカードが置いてあるから,3番目が4から10のカードである確率は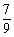 となります。
となります。